Oefenvragen wiskunde

Instructies

Dit korte oefen-tentamentje voor wiskunde bestaat uit 10 meerkeuzevragen, 3 open vragen, en 1 (meerkeuze) vraag over functies schetsen. Kies bij de meerkeuzevragen het juiste antwoord en beantwoord de open vragen met een getal.

Meerkeuzevragen

  1. Wat is de afgeleide van \(f(x) = x^3 + 10x\)?
      1. \(3x^2 - 10\)
      1. \(x^2 + 10\)
      1. \(3x + 10\)
      1. \(2x^3 + 10\)
      1. \(3x^2 + 10\)
  2. Schrijf op als één breuk: \(\frac{3}{4a} + \frac{1}{2b}\)
      1. \(\frac{2b + 4a}{8a}\)
      1. \(\frac{5b}{4a}\)
      1. \(\frac{6b + 4a}{8ab}\)
      1. \(\frac{1b}{2a}\)
      1. \(\frac{3b}{2ab}\)
  3. De limiet van \(\frac{1}{x}\)als \(x \to \infty\)is:
      1. \(1\)
      1. \(0\)
      1. \(\infty\)
      1. \(-\infty\)
      1. \(\text{Geen van allen}\)
  4. Wat is \({^{10}\log{(1000)}}\)?
      1. 2
      1. 3
      1. 4
      1. 10
  5. Welke van de volgende functies heeft een verticale asymptoot bij \(x = a\)?
      1. \(x + a\)
      1. \(\frac{1}{x-a}\)
      1. \(x^2 - a\)
      1. \(\log({a \over x})\)
  6. Wat is de afgeleide van \(e^x\)?
      1. \(x e^x\)
      1. \(e^{x-1}\)
      1. \(e^x\)
      1. \(xe^{x-1}\)
  7. Los op: \(\frac{a}{x} = 7q\)
      1. \(x = \frac{a}{q}\)
      1. \(x = \frac{a}{7q}\)
      1. \(x = q\)
      1. \(x = a\)
  8. Wat is de horizontale asymptoot van \(f(x) = \frac{3x}{x+2}\)?
      1. \(y = 3\)
      1. \(y = 2\)
      1. \(y = 0\)
      1. \(y = \infty\)
  9. Los op: \(3^x = 27\)
      1. \(x = 3\)
      1. \(x = 9\)
      1. \(x = 2\)
      1. \(x = 4\)
  10. Welke van deze functies heeft GEEN asymptoot?
      1. \(f(x)=\frac{x}{x-b}\)
      1. \(f(x)=\frac{q}{x+a}\)
      1. \(f(x)=\frac{r}{x}\)
      1. \(f(x)=bx^2\)

Open vragen

  1. Bepaal de hellingshoek van de functie \(f(x)=3x^2\) bij \(x=2\)

  2. Los de vergelijking \(2^{x+1} = 16\) op.

  3. Bepaal de limiet: \(\lim_{x \to 0} \frac{ax}{x+2}\).

Grafiek matchen

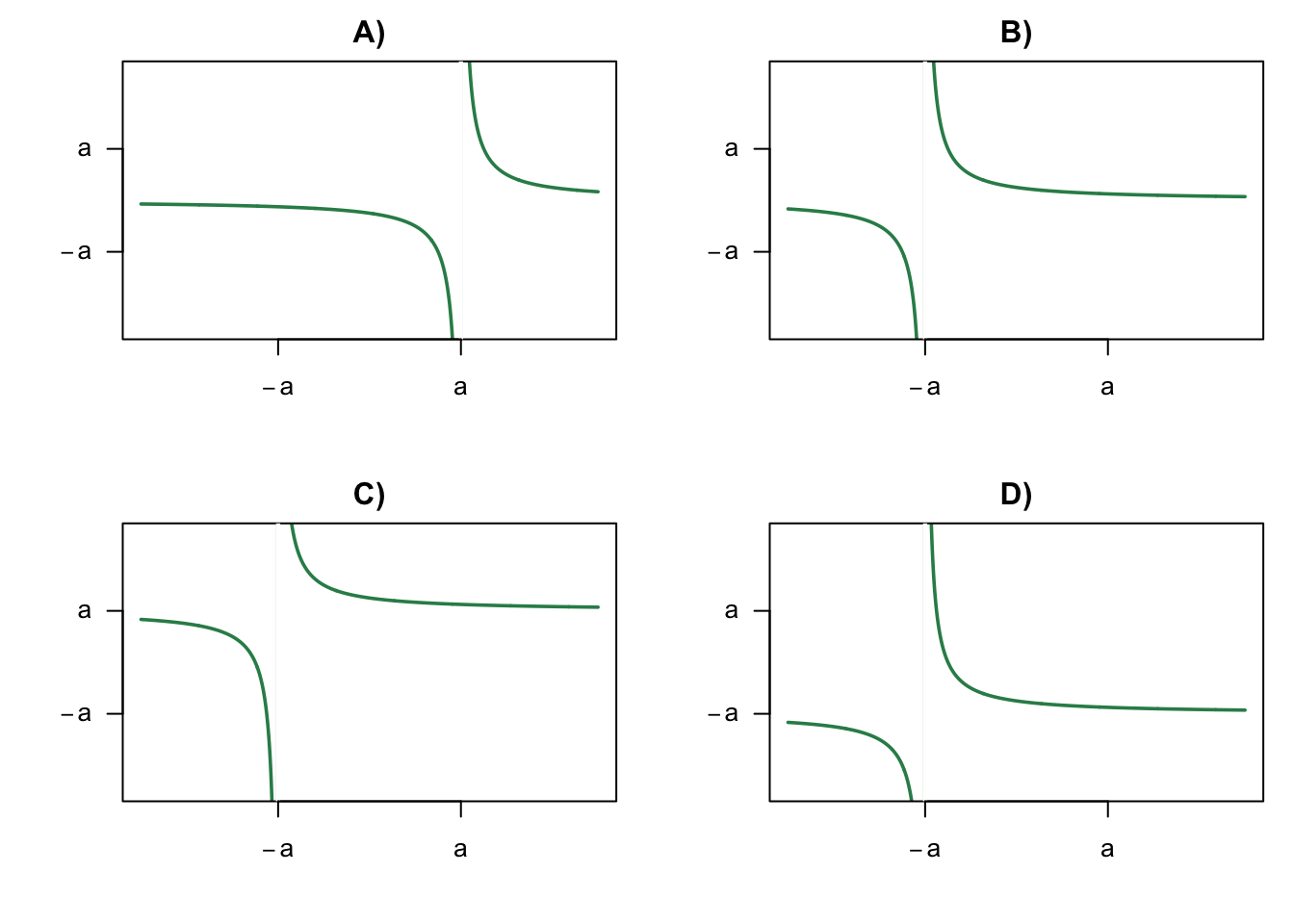
  1. Welke van de onderstaande grafiek past bij de functie \(f(x)=\frac{1}{x-a}\)?