x <- 10
a <- 1
y <- x+a
print(y)Introductie
Leerdoelen
Aan het eind van dit introducerende hoofdstuk, word je geacht het volgende te kunnen:
- Uitleggen waarom modellen een belangrijk stuk gereedschap zijn binnen de biologie
- De drie basisingrediënten van elk model benoemen
- Onderscheid maken tussen onderwerp (wat gemodelleerd wordt) en modelformalismen (hoe er gemodelleerd wordt)
- Voorbeelden van verschillende modelformalismen geven, en alvast enkele aannames die erbij komen kijken benoemen (nog niet in detail: gedurende de cursus leer je meer over de details)
- Uitleggen wanneer een model “goed” is
Onze intuïtie is niet genoeg
Waarom zijn er het ene jaar zoveel meer konijnen dan het andere jaar? Hoe worden de patronen op de huid van een zebravis aangelegd? Komt het afschieten van runderen in de Oostvaarderseplassen om de populatiegrootte te beheersen het welzijn van de dieren ten goede? Wat is er aan de hand tijdens een hartritmestoornis, en op welke manieren kunnen we het hartritme weer herstellen? Dit zijn allemaal belangrijke biologische vraagstukken, maar zoals jullie allemaal weten zijn biologische systemen vaak erg ingewikkeld. In het vakgebied Theoretische Biologie worden daarom modellen en simulaties gebruikt, om inzicht te vergaren en zodoende betere voorspellingen te kunnen doen. Omdat modellen een steeds belangrijker onderdeel zijn van de biologie, is het voor elke bioloog belangrijk om de nodige basiskennis te hebben.
Om echt goed te begrijpen wat een model is, gaan we helemaal bij de basis beginnen en de meest simpele modellen bespreken. Je zal zien dat zelfs simpele modellen zich vaak onvoorspelbaar of tegenintuïtief kunnen gedragen. Dit vertelt ons meteen al dat onze eigen intuïtie er zelfs voor schijnbaar simpele systemen vaak naast zit en modellen dus essentiëel zijn om te kijken hoe een systeem nou eigenlijk werkt! Daarom gaan we in dit cursusonderdeel leren hoe je modellen moet lezen (wiskunde en simpele R-scripts), en welke conclusies je er wel/niet uit kan trekken. Hiervoor bespreken we modellen uit verschillende vakgebieden binnen de biologie (microbiologie, ecologie, gedrag, evolutie, en nog veel meer). Wat je favoriete onderwerp ook is: je komt als bioloog – ook na deze cursus – zeer zeker nog meer met modellen in aanraking!
Planning “Biologische modellen”
Dit cursusonderdeel is verdeeld over 9 genummerde hoofdstukken, die we gedurende drie weken bespreken:
- Week 1:
- Week 2:
- Week 3:
Elke dag bespreken we in de hoorcolleges het onderwerp van een hoofdstuk (en eventuele aanvulling), waarna jullie tijdens het werkcollege vragen beantwoorden over de stof. Daarnaast is er dinsdag- en donderdagmiddag ruimte voor zelfstudie, en gaan jullie tijdens de laatste week een verslag over een mini-project schrijven. Een volledig overzicht van de planning, vind je hier.
Wat is een model eigenlijk?
Maar voordat we aan deze modules beginnen, wil ik jullie eerst graag uitleggen wat modellen nou eigenlijk zijn.
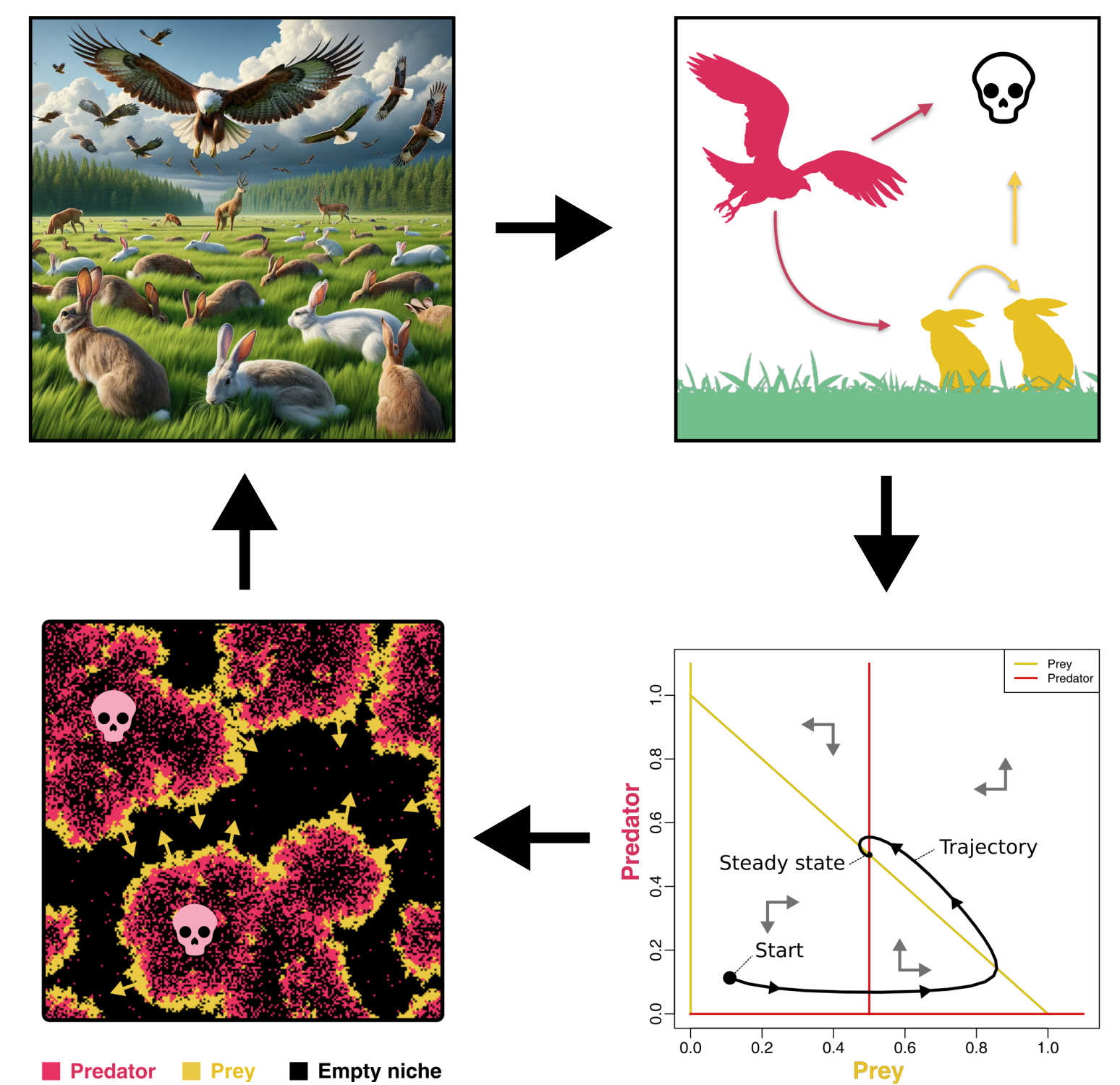
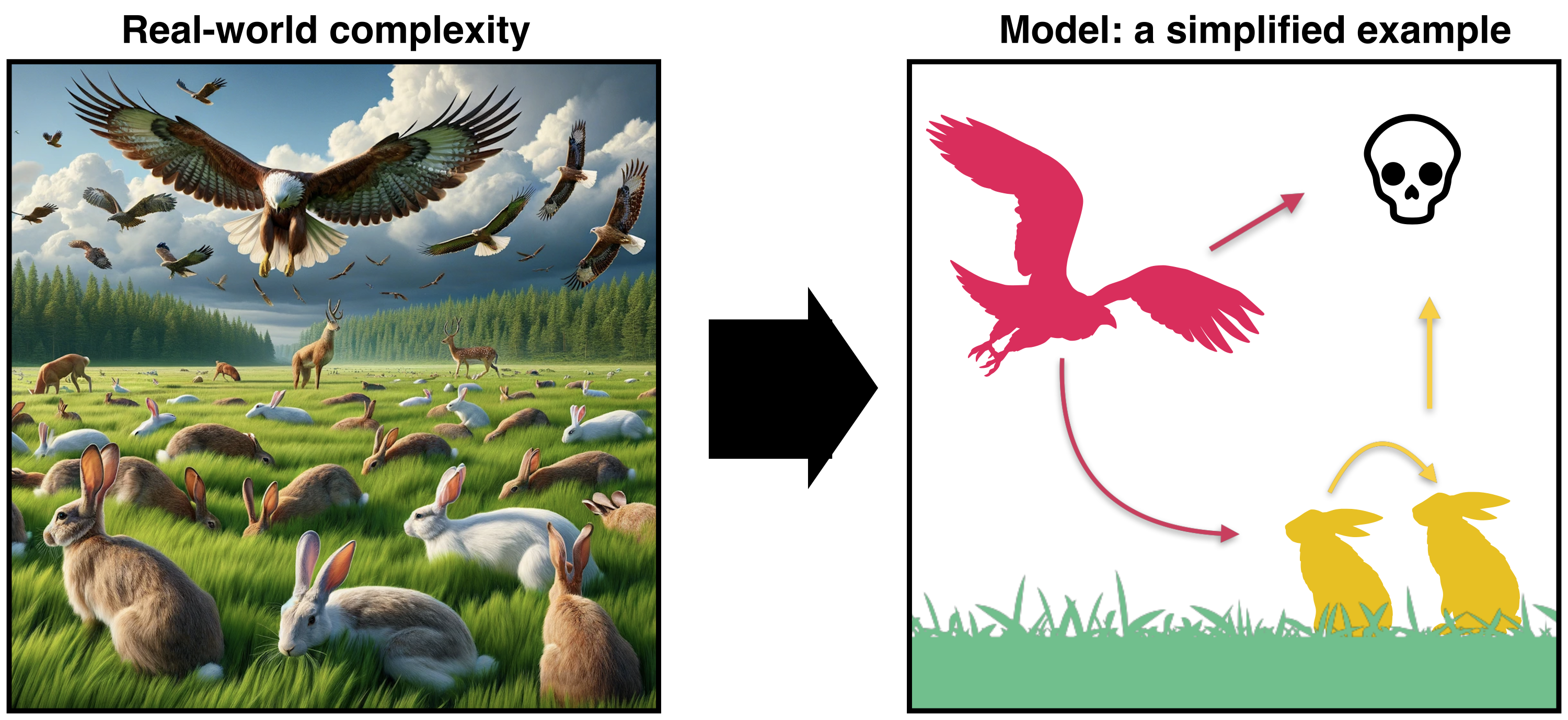
Stel je voor dat je op de Veluwe aan het wandelen bent, en het scenario tegenkomt aan de linker zijde van Figuur 1: overal lopen verschillend gekleurde konijnen, roofvogels vliegen rond en grijpen hun kans, en in de achtergrond zie je herten, naaldbossen, en duistere wolken. Hoewel dit scenario natuurlijk een enorme karikatuur is, worden we in de biologie wel vaak geconfronteerd met dit probleem: biologische systemen bestaan uit veel onderdelen die allemaal tegelijk elkaar beïnvloeden. Om een model te bouwen dat ons helpt beter te begrijpen wat hier gebeurt is het allereerst belangrijk om te bepalen wat in dit (eco)systeem essentieel is voor wat we willen begrijpen. Op die manier zal het te bouwen model een versimpeling van de complexe realiteit zijn die makkelijker te analyseren en begrijpen is. Zo zie je aan de rechter zijde van Figuur 1 dat we de achtergrond (herten, bos, wolken) even vergeten, en ons richten op slechts een paar onderdelen. Wellicht zijn we vooral geïnteresseerd in de interacties tussen de roofvogels en de konijnen. De roofvogels jagen op konijnen, terwijl de konijnen doen waar konijnen goed in zijn: vermenigvuldigen.
In de biologie zijn we veelal geïnteresseerd in de dynamiek van systemen. Dat betekent: hoe verandert het systeem over de tijd? In het voorbeeld van de roofvogels en konijnen, kunnen we ons bijvoorbeeld afvragen welk van de twee soorten zal toenemen, en welke zal afnemen. Je kunt je natuurlijk wel voorstellen dat als er heel veel konijnen zijn, dat de roofvogels dan een enorme kans hebben konijnen te vangen, en dus in populatiegrootte zullen toenemen. Echter zal dit het aantal konijnen verlagen… wat gebeurt er daarna? Sterven alle konijnen uit? Kunnen ze samen voortbestaan? Om dit te bepalen (en te kijken waar dit van af hangt) kunnen we binnen het model variëren met hoe lang een roofvogel leeft, of konijnen ook van ouderdom dood gaan, hoe veel konijnen een roofvogel kan eten, en of de dynamica van grasgroei ook belangrijk is. Dit betekent dat we moeten variëren met de onderdelen waaruit elk model bestaat: variabelen, parameters, en aannames (assumptions).
Net zoals bij elk vakgebied, komen er bij modellen veel nieuwe termen kijken. Dit jargon is niet altijd goed in het Nederlands te vertalen, en daarnaast zijn de Engelse termen vaak heel handig om te kennen. Om jullie daarmee te helpen, zullen we toch vaak het Engelse jargon gebruiken. Aan het einde van ieder hoofdstuk staat een tabel met de vertaling van deze termen, en wat deze precies betekenen.
De basisingrediënten van elk model
Modellen in de biologie kunnen heel simpel zijn, maar soms ook vrij complex zijn. Hoe ingewikkeld of simpel een model ook is, de basisingrediënten veranderen eigenlijk nauwelijks. Elk model draait om:
Variabelen (variables): hetgeen wat er verandert (bijvoorbeeld over de tijd). In het voorbeeld hierboven zouden dat bijvoorbeeld de populatiegroottes van de konijnen en/of roofvogels kunnen zijn, en eventueel zelfs de hoeveelheid gras.
Parameters (parameters): constante waarden die bepalen hoe variabelen veranderen, bijvoorbeeld de groeisnelheid van de konijnen of de sterftesnelheid van predatoren. In plaats van deze getallen vast te zetten (bijv. groeisnelheid = 2) gebruiken we meestal zogenoemde “vrije parameters” (bijv. groeisnelheid = \(r\)). Let op: in biologische modellen nemen we over het algemeen aan dat dergelijke parameters positief zijn. Hoewel sterfte wiskundig gezien een “negatief” begrip is (de populatie neemt immers af) is de parameter waarmee we sterfte bepalen (bijvoorbeeld \(d\) voor death rate) positief.
Aannames (assumptions): keuzes die we maken om het model eenvoudig te houden. In het voorbeeld hierboven negeren we bijvoorbeeld de herten, het bos op de achtergrond, en we zouden ook kunnen kiezen om alle konijnen in het model identiek te laten zijn, ook al zien we in werkelijkheid variaties in hun kleur die eventueel de predatiekans beïnvloedt. Of konijnen wel/niet van nature dood gaan, is een aanname die we kunnen variëren. Zodoende kunnen we meer inzicht krijgen in welke componenten belangrijk zijn.
Aan het eind van dit cursusonderdeel zul je begrijpen dat de bovengenoemde begrippen gebruikt kunnen worden om allerlei biologische scenario’s simpeler te omschrijven. Door deze versimpelingen te bestuderen, proberen we wat te leren over biologie. Maar let op: afhankelijk van de biologische situatie kan het zijn dat aannames meer of minder gepast zijn! Of een aanname gepast is, zal dus liggen aan de precieze vragen die we stellen.
Aan het eind van elk hoofdstuk staan lange verdiepende vragen, die we in het werkcollege behandelen. Tussen het lezen door staan echter soms ook wat kortere vragen, zodat je kan inschatten of je de stof goed tot je hebt genomen. Dus hierbij:
Oefening 1 (Bloedsuikerspiegel tijdens het sporten)
Tijdens het sporten daalt de bloedsuikerspiegel \(a\) met een vaste snelheid \(b\), waarbij een eiwit \(c\) tot expressie komt met vaste snelheid \(d\).
a. Welke van de symbolen (\(a\), \(b\), \(c\), en \(d\)) zou je als variabelen kunnen beschouwen, en waarom?
b. Welke van deze symbolen zou je eerder als parameters beschouwen, en waarom?
Nu we een idee hebben wat paramteres, variabelen, en aannames precies zijn, gaan we een paar voorbeeld-scenarios bespreken. Let op: deze voorbeelden hoef je nu nog niet 100% te begrijpen, en dienen op dit punt vooral ter illustratie.
Een verschillend model voor elk scenario
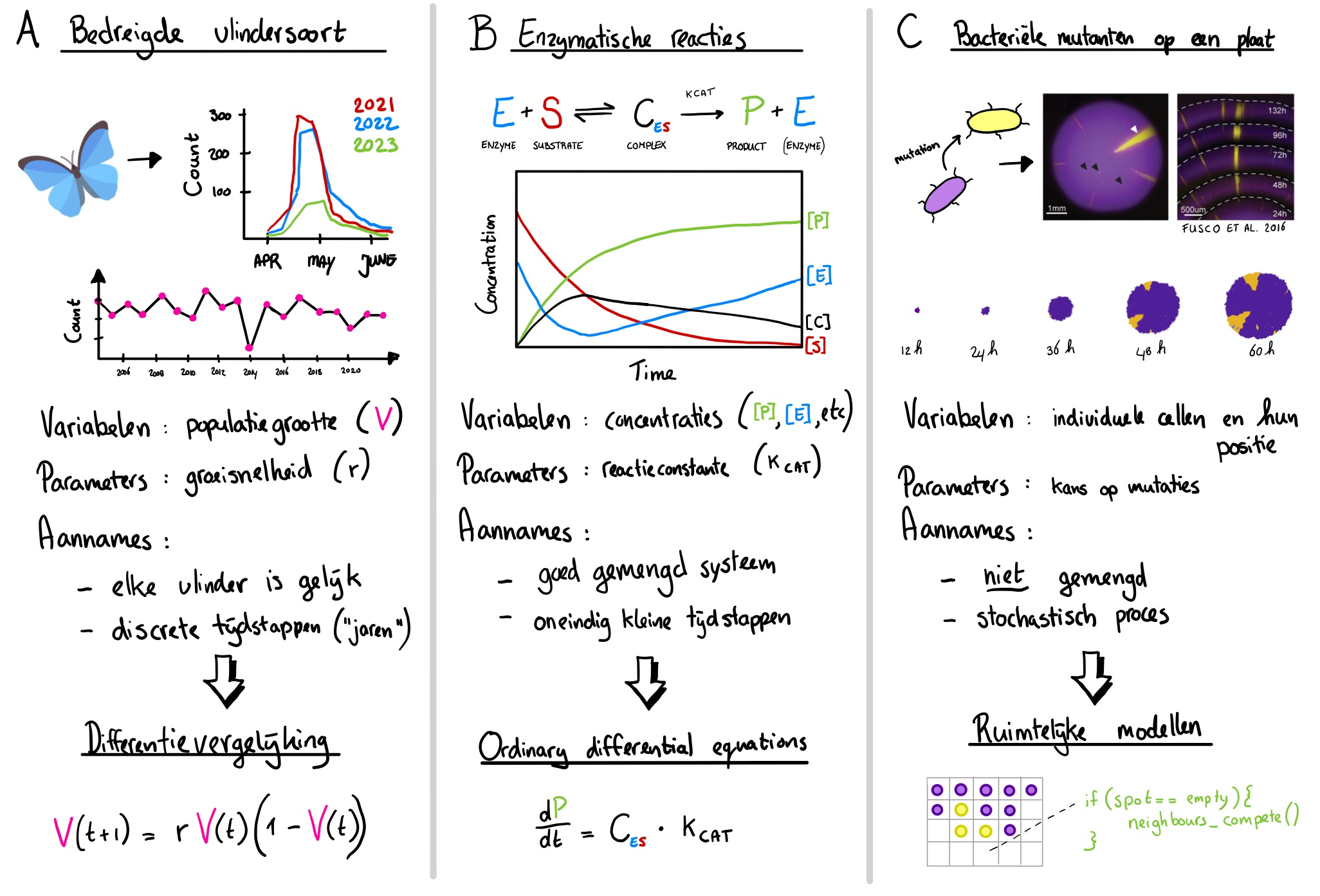
Niet alle modellen zien er hetzelfde uit. Veel modellen gebruiken simpele wiskundige formules om verandering over de tijd te omschrijven. Zo zouden we de jaarlijkse populatiegrootte van een bedreigde vlindersoort (zie Figuur 2 A) kunnen omschrijven in een differentievergelijking (Difference Equation, ook wel Map genoemd). Deze vergelijking omschrijft simpelweg een relatie tussen de huidige waarde van de variabele \(V(t)\) (hoeveelheid vlinders in dit jaar) en de toekomstige waarde van de variabele \(V(t+1)\) (hoeveelheid vlinders over 1 jaar). In het volgende hoofdstuk zul je leren hoe eenvoudig het is om met deze vergelijkingen te werken, en deze in een simpel R-script te bestuderen.
Ondanks de eenvoud van differentievergelijkingen, werken we in de biologie echter meestal met een ander type wiskundig model: differentiaalvergelijkingen. In de literatuur zul je deze modelvorm tegenkomen onder de noemer Ordinary Differential Equations (ODEs). Deze modellen omschrijven niet discrete tijdstappen (jaar 1, jaar 2, etc.), maar omschrijven in plaats daarvan de snelheid waarmee de variabelen veranderen. Zo kun je bijvoorbeeld chemische reactiesnelheden goed beschrijven met ODEs, en op die manier bestuderen hoe enzymkinetiek werkt (Figuur 2 B). Omdat veel biologische processen goed uit te drukken zijn in termen van snelheden (groeisnelheid, reactiesnelheid, hormoon-productie per uur, etc.), is dit type model erg populair om simpele biologische processen te modelleren. Daarom gaan we in deze cursus uitgebreid bespreken hoe je dit type model kan lezen, en hoe je er biologische conclusie uit kan trekken.
Hoewel ODEs populair zijn binnen de biologie, is er in de laatste jaren steeds meer aandacht gekomen voor ruimtelijke patronen (spatial patterns). Wat hebben bijvoorbeeld de strepen van een zebravis te maken met de patronen van struikgewassen op de toendra? Op het eerste gezicht misschien niets, maar het blijkt dat je beide patronen kan verklaren met hetzelfde mechanisme! Dergelijke patronen kunnen belangrijk zijn voor natuurbehoud, en in het laatste hoofdstuk zal je zelfs zien dat er belangrijke medische consequenties zijn. Het kan dus zeer nuttig zijn om beter te begrijpen hoe patroon-vorming werkt. Hiervoor gebruiken we ruimtelijke modellen (spatial models) (Figuur 2 C).
Aan het eind van dit cursusonderdeel zal je veel verschillende modellen voorbij hebben zien komen: zowel simpele, wiskundige modellen zoals die in Figuur 2 A/B, als variaties op ruimtelijke modellen zoals die in Figuur 2 C. Het overkoepelende doel is is dan ook dat je basiskennis hebt over deze modellen, begrijpt waarom ze belangrijk zijn binnen de biologie, en dat je kan je uitleggen welk type model het beste past om een specifiek biologisch scenario te omschrijven.
Oefening 2 (Modeluitkomsten)
Elk type model heeft andere modeluitkomsten: wiskundige modellen hebben vaak vooral voorspellingen van veranderende aantallen, terwijl ruimtelijke modellen ook patronen als resultaat hebben.
a. Waarom denk je dat een groeiende biofilm meestal niet met ODEs wordt gemodelleerd?
b. Waarom denk je dat een goed gemengde fles bacterien meestal niet met een ruimtelijk model bestudeerd wordt?
c. Waar zou je de vorming van korstmossen mee kunnen modelleren?
Wanneer is een model “goed”?
Omdat modellen versimpelingen zijn, zullen ze nooit alle details uit de biologie beschrijven. Dit is ook niet het doel van modellen. In plaats daarvan proberen we, ondanks de versimpelingen, iets over biologie te leren, of voorspellingen te doen. Een model is daarom niet per se slecht als het onrealistische aannames doet, omdat het best kan zijn dat je er toch iets heel belangrijks van leert, of dat de voorspellingen betrouwbaar zijn. De Britsche statisticus George P. Box zei daarom ooit het volgende over modellen:
“All models are wrong, but some are useful.”
– George P. Box
Als je nog niet helemaal begrijpt waarom zelfs onrealistische modellen nuttig kunnen zijn, dan is dat niet erg. In dit cursusonderdeel gaan we stapje voor stapje leren werken met modellen, en je zult zien dat deze manier van denken niet alleen heel nuttig, maar ook heel leuk kan zijn!
Opgaven
Misschien is het je opgevallen dat niet alle opgaven dezelfde kleur hebben. We gebruiken namelijk een kleurcodering zodat je meteen weet of het een algemene vraag is, of dat je aan de slag gaat met pen-en-papier of R. Algemene (open) vragen zijn oranje, en zien er uit zoals Oefening 3. Opgaven die je met pen en papier moet maken, zijn geel gekleurd en hebben een potlood-icoontje (zie Oefening 4). Opgaven die je met R moet maken (of andere computeropgaven), zien er uit als Oefening 5. Er ook gemengde vragen, waarbij je beide vaardigheden toepast. Deze zien er uit als Oefening 6.
Dit introducerende hoofdstuk heeft geen opgaven.
Oefening 3 (Een open vraag)
Bijvoorbeeld: leg uit waarom in de biologie modellen worden gebruikt.
Oefening 4 (Pen en papier opgave)
Bijvoorbeeld: vind de twee oplossingen voor de vergelijking \(x(1-x)=0\).
Oefening 5 (R opgave)
Bijvoorbeeld: neem de volgende code over en pas aan:
Oefening 6 (Een gemengde vraag)
Bijvoorbeeld:
a. Schets de functie \(f(x)=1+ax\)
b. Controlleer je antwoord met het onderstaande R script
a=0.1
func <- function(x){
return(1+a*x)
}
curve(func,-3,10,ylim=c(0,5),xlim=c(-3,10),lwd=2,col="seagreen")
abline(h=0,col="grey")
abline(v=0,col="grey")Terminologie
| Nederlands | Engels | Beschrijving |
|---|---|---|
| Model | Model | Een versimpeling van een systeem, bijvoorbeeld in de vorm van eenvoudige wiskunde of computerprogramma’s |
| Dynamiek | Dynamics | Hoe dingen (variabelen) veranderen. Meestal zijn we geinteresseerd in veranderingen over de tijd, maar soms ook in veranderingen over de ruimte |
| Variabele | Variable | Wat er verandert, bijvoorbeeld het aantal bacteriën tijdens exponentiële groei |
| Parameter | Parameter | Constante waardes die de dynamiek bepalen, bijvoorbeeld de verdubbelingstijd van bacteriën |
| Model-uitkomsten | Modelling outcomes | Wat voor type resultaten je model kan opleveren. Wiskundige modellen geven kwantitatieve of kwalitatieve uitkomsten, terwijl ruimtelijke modellen daarnaast ook patronen als uitkomst hebben. |
| Aanname | Assumption | Een keuze die we maken om het model eenvoudig te houden |