# beginaantal rijst
R <- 1
# herhaal iets 63 keer met een for-loop
for (i in 1:63) {
R[i+1] <- R[i]*1.05 # R in het volgende hokje is 1.05*R in deze stap
}
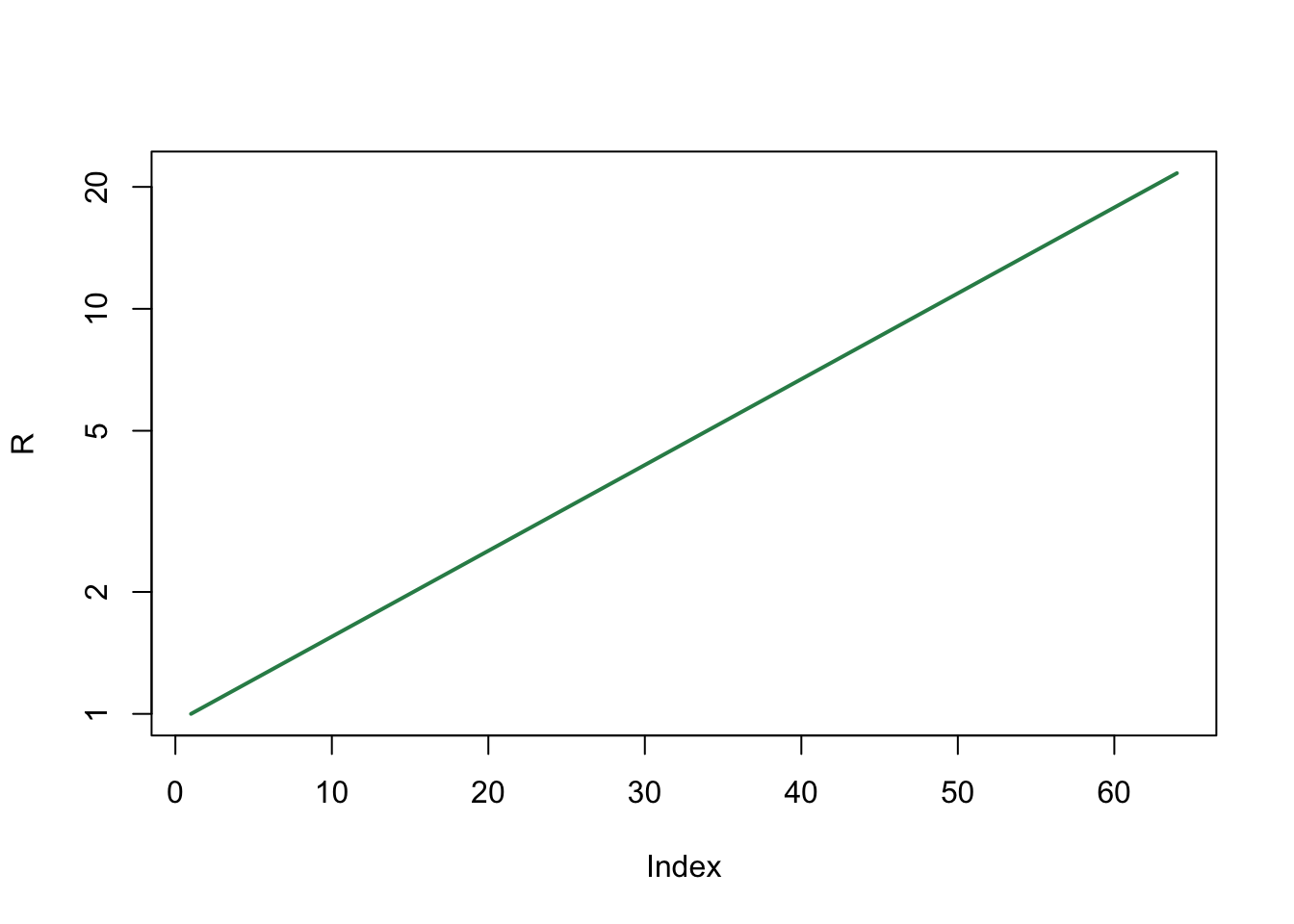
plot(R , type='l', col="seagreen", log="y", lwd=2) 
Antwoorden modellen
Antwoorden introductie
a. De dingen die veranderen (bijvoorbeeld over de tijd) noemen we variabelen. De dingen die veranderen zijn hier je bloedsuikerspiegel (a) en de hoeveelheid eiwit (c), dus dit zijn de variabelen.
b. De snelheden (b en d) waarmee de variabelen veranderen, staan volgens de omschrijving vast, en zijn dus parameters.
a. Eén van de aannames van een ODE-model is dat het systeem goed gemengd is (Figuur 2B). Naast de groeisnelheid is de ruimtelijke structuur bij een biofilm ook relevant, we voldoen dus niet aan de aanname van een goed gemengd systeem. Daarom is het beter om een ruimtelijk model te gebruiken voor het modelleren van een biofilm.
b. Door goed te mengen zijn posities niet belangrijk, dus het modelleren van posities is dus niet inzichtelijk, en gaat hooguit veel tijd kosten (voor jou of voor de computer). Het is beter om dit systeem met bijvoorbeeld een ODE te beschrijven.
c. De vorming van korstmossen is een proces waarbij ruimte belangrijk is, het is geen goed gemengd systeem. Een ruimtelijk model is dus het meest geschikt.
Antwoorden 10 Exponentiële groei
a. Ja, het percentage is klein maar de groei is alsnog exponentieel! Dit kun je zien doordat de hoeveelheid rijst per vakje met een rechte lijn toeneemt op een log-lineaire schaal. Daarnaast hebben we aan de vorm van de formule niks veranderd, we hebben alleen de groeisnelheid kleiner gemaakt.
b. Door de rijstkorrels in elke vakje bij elkaar op te tellen kunnen we uitrekenen hoeveel rijstkorrels je in totaal hebt:
sum(R)[1] 434.0933Zoals je ziet hebben we nu een stuk minder rijstkorrels dan bij het voorbeeld met verdubbeling. We hebben er nu (naar beneden afgerond) 434.
a.
# Stap 1: Stel begin-aantal konijnen en de groeisnelheid in
N <- 24
r <- 2
# verdubbel het aantal konijnen 20 keer
for (i in 1:20){
N <- r*N
}
# er zijn verschillende opties om "Het aantal konijnen na 20 tijdstappen is gelijk aan 25165824” te printen:
# met cat:
cat("Het aantal konijnen na 20 tijdstappen is gelijk aan ", N)Het aantal konijnen na 20 tijdstappen is gelijk aan 25165824# met paste:
paste("Het aantal konijnen na 20 tijdstappen is gelijk aan ", N)[1] "Het aantal konijnen na 20 tijdstappen is gelijk aan 25165824"b.
# Stap 1: Stel begin-aantal konijnen in
N <- 24
# Stap 2: Verdubbel het aantal konijnen 30 keer
for (t in 1:30){
N[t+1] <- 2*N[t]
}
# Stap 3: Plot het resultaat
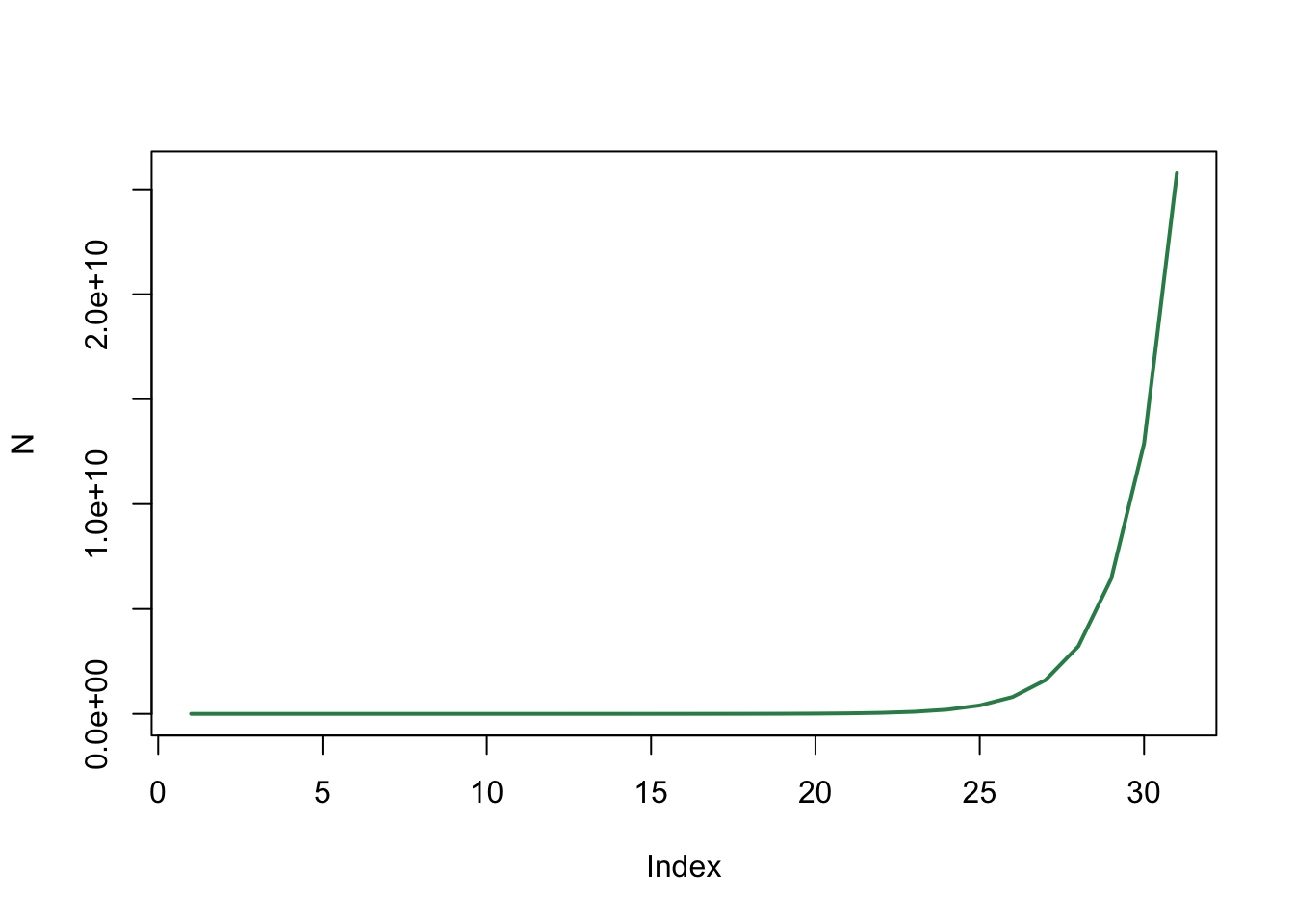
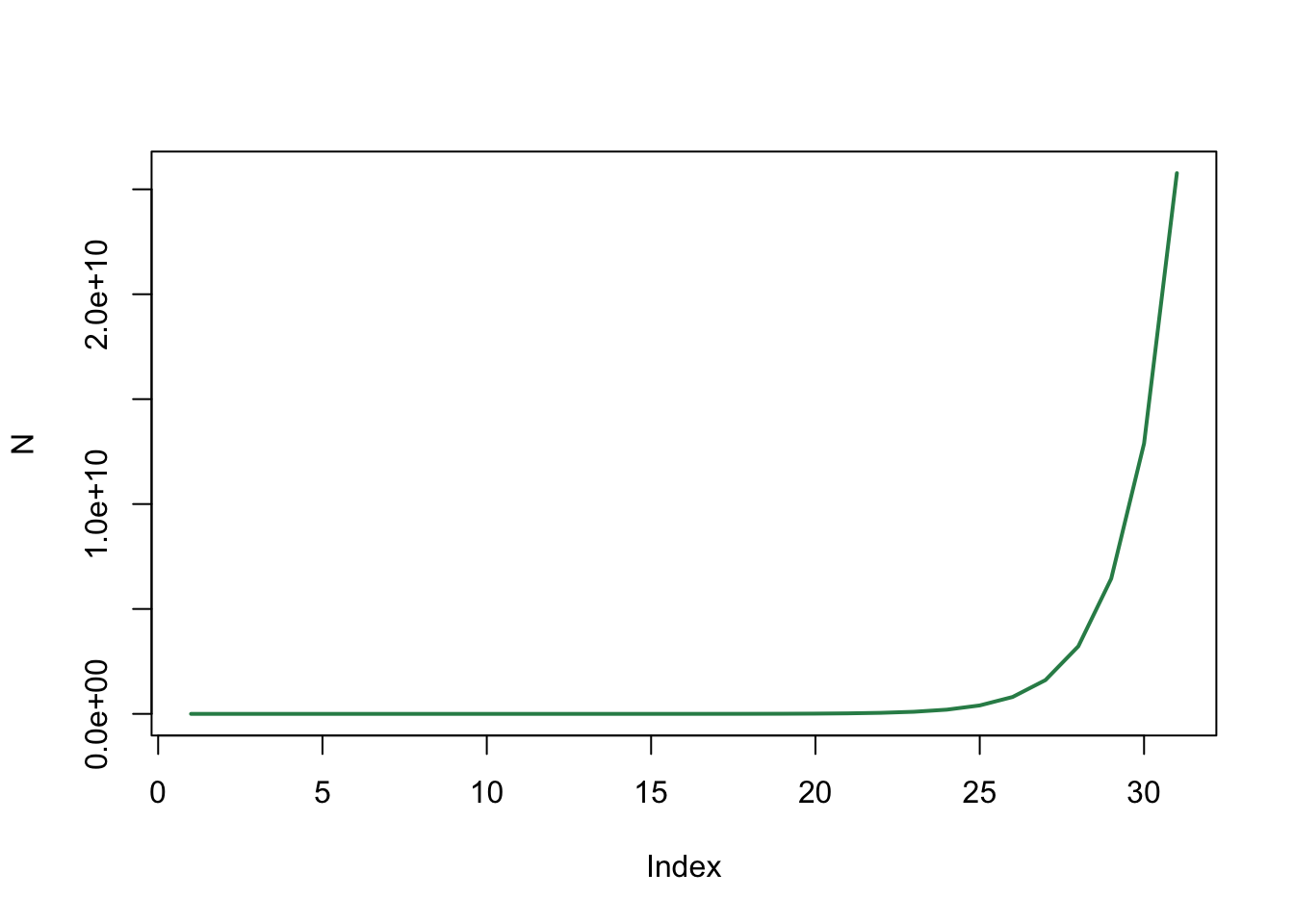
plot(N, type='l', col="seagreen", lwd=2)
De toename van het aantal konijnen lijkt exponentieel te zijn. Door de y-as log-lineair te maken kunnen we dit zeker weten:
# Stap 1: Stel begin -aantal konijnen in
N <- 24
# Stap 2: Verdubbel het aantal konijnen 30 keer
for (t in 1:30){
N[t+1] <- 2*N[t]
}
# Stap 3: Plot het resultaat met een logaritmische y as, net zoals in de code van figuur 3
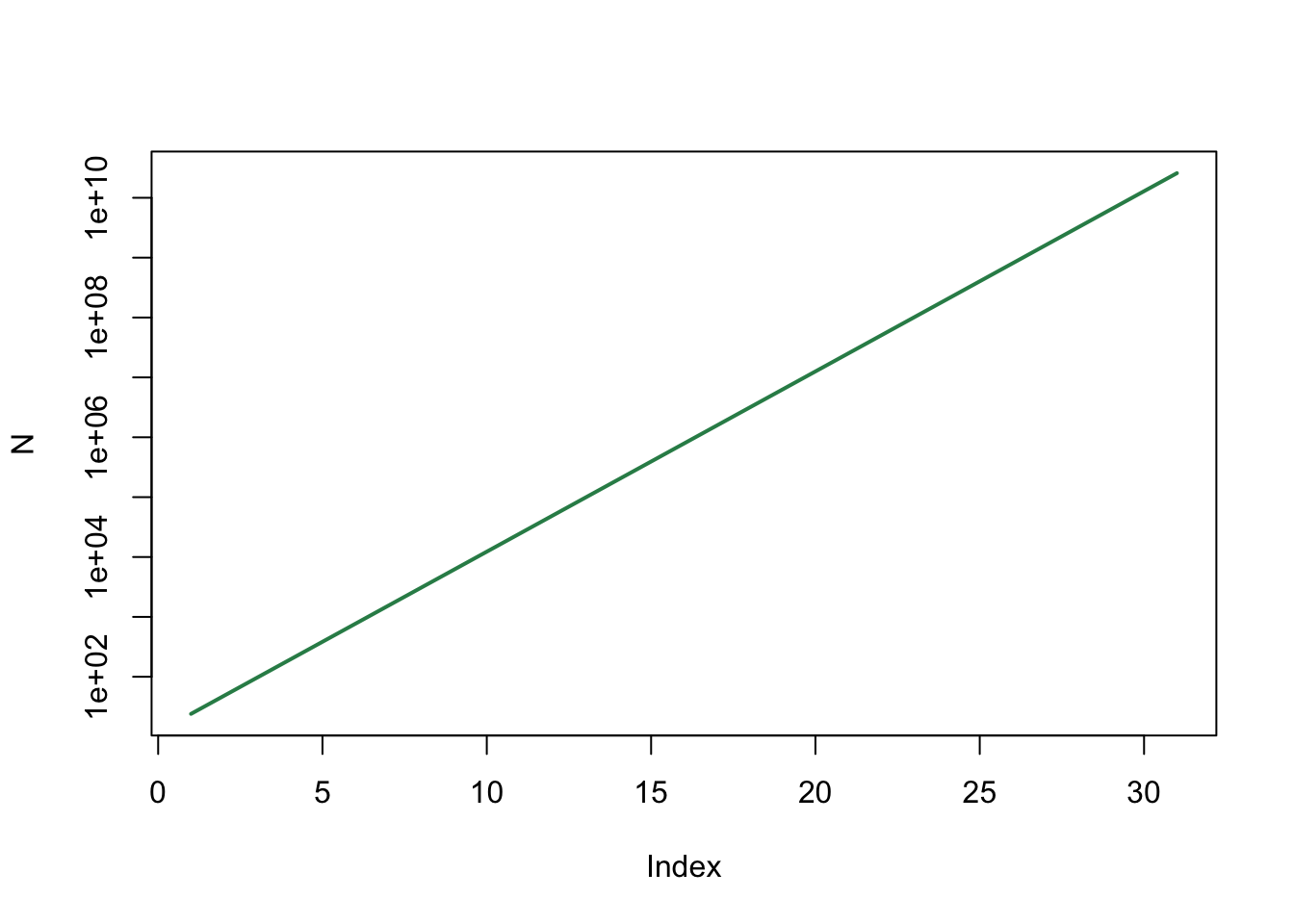
plot(N , type='l', col="seagreen", lwd=2, log="y")
Met een logaritmische schaal op de y-as krijgen we een rechte lijn en weten we nu zeker dat we met exponentiële groei te maken hebben.
Wanneer \(r<1\) (bijvoorbeeld \(r=0.9\)) zien we juist exponentiële afname van de konijnen populatie.
c.
# Stap 1: Stel begin-aantal konijnen in, en een birth en death rate
N <- 24
b <- 2
d <- 0.1
# Stap 2: Verdubbel het aantal konijnen 30 keer
for (t in 1:30){
N[t+1] <- b*N[t] - d*N[t]
}
# Stap 3: Plot het resultaat
plot(N, type='l', log="y", col="seagreen", lwd=2)
We zien dat er nog steeds sprake is van exponentiële groei, omdat we met een logaritmische y-as een rechte lijn krijgen.
d.
# Stap 1: Stel begin-aantal konijnen in, en een birth en death rate
N <- 24
b <- 2
d <- 1.1
# Stap 2: Verdubbel het aantal konijnen 30 keer
for (t in 1:30){
N[t+1] <- b*N[t] - d*N[t]
}
# Stap 3: Plot het resultaat
plot(N, type='l', col="seagreen", lwd=2)Dit is hetzelfde resultaat als bij vraag b met \(r<1\)! Nu kunnen we dit echter uitdrukken in termen van geboorte en sterfte. Hoewel er elke tijdstap een toenname is van 100%, is er ook een afname van 110%! De konijnen gaan dus sneller dood dan ze zich voort kunnen planten, dus is er exponentiële afname.
e. Invullen van \(N(t)=24\), \(b=2\) en \(d=0.001\) geeft:
\[\begin{align*} N(t+1) &= b \cdot N(t) - d \cdot N(t)^2 \\ N(t+1) &= 2 \cdot 24 - 0.001 \cdot 24^2 \\ N(t+1) &= 48 - 0.001 \cdot 576 \\ N(t+1) &= 48 - 0.576 \\ N(t+1) &= 47.424 \end{align*}\]
De geboorteterm is dus 48, en de sterfteterm slechts 0.576. Er worden dus wel veel nieuwe konijnen geboren, maar er gaan er maar weinig (een half konijn) dood. De volledige vergelijking (de hoeveelheid konijnen in de volgende tijdstap) is dus 47.424. De populatie zal dus – beginnende met 24 konijnen – groeien. Later in de cursus komen we terug op het feit dat er natuurlijk geen “halve konijnen” dood kunnen gaan.
f. Invullen van \(N(t)=1000\), \(b=2\) en \(d=0.001\) geeft:
\[\begin{align*} N(t+1) &= b \cdot N(t) - d \cdot N(t)^2 \\ N(t+1) &= 2 \cdot 1000 - 0.001 \cdot 1000^2 \\ N(t+1) &= 2000 - 0.001 \cdot 10^6\\ N(t+1) &= 2000 - 1000 \\ N(t+1) &= 1000 \end{align*}\]
Ook nu worden er veel nieuwe konijnen geboren (2000), maar er gaan ook veel konijnen dood (1000). In totaal is de populatie in de volgende tijdstap dus 1000 geworden, en dat was al zo! Bij 1000 konijnen verwachten we dus een evenwichtshoeveelheid konijnen.
g.
\[\begin{align*} N = bN - dN^2 \\ 1 = b - dN \\ dN = b - 1 \\ N = {(b - 1) \over d} \\ \end{align*}\]
Met de parameters \(b=2\) en \(d=0.001\) geeft dit \(\bar{N} (\text{N in evenwicht})=\frac{2-1}{d} = \frac{1}{d}\). Het systeem is dus in evenwicht als er 1000 konijnen zijn.
h.
# Stap 1: Stel begin-aantal konijnen in
N <- 24
b <- 2
d <- 2e-9
# Stap 2: Verdubbel het aantal konijnen 30 keer
for (t in 1:30){
N[t+1] <- b*N[t] - d*N[t]^2
}
# Stap 3: Plot het resultaat
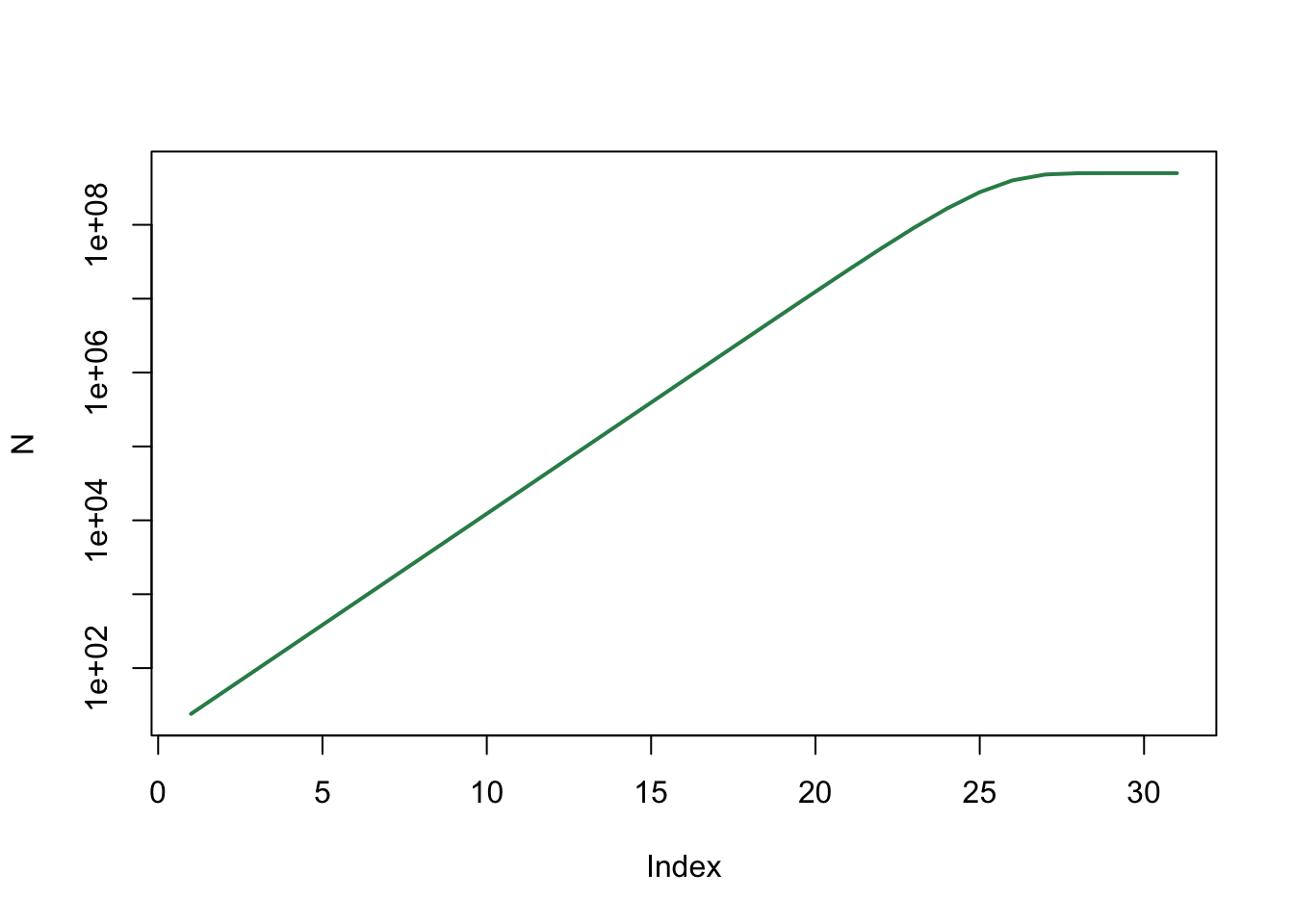
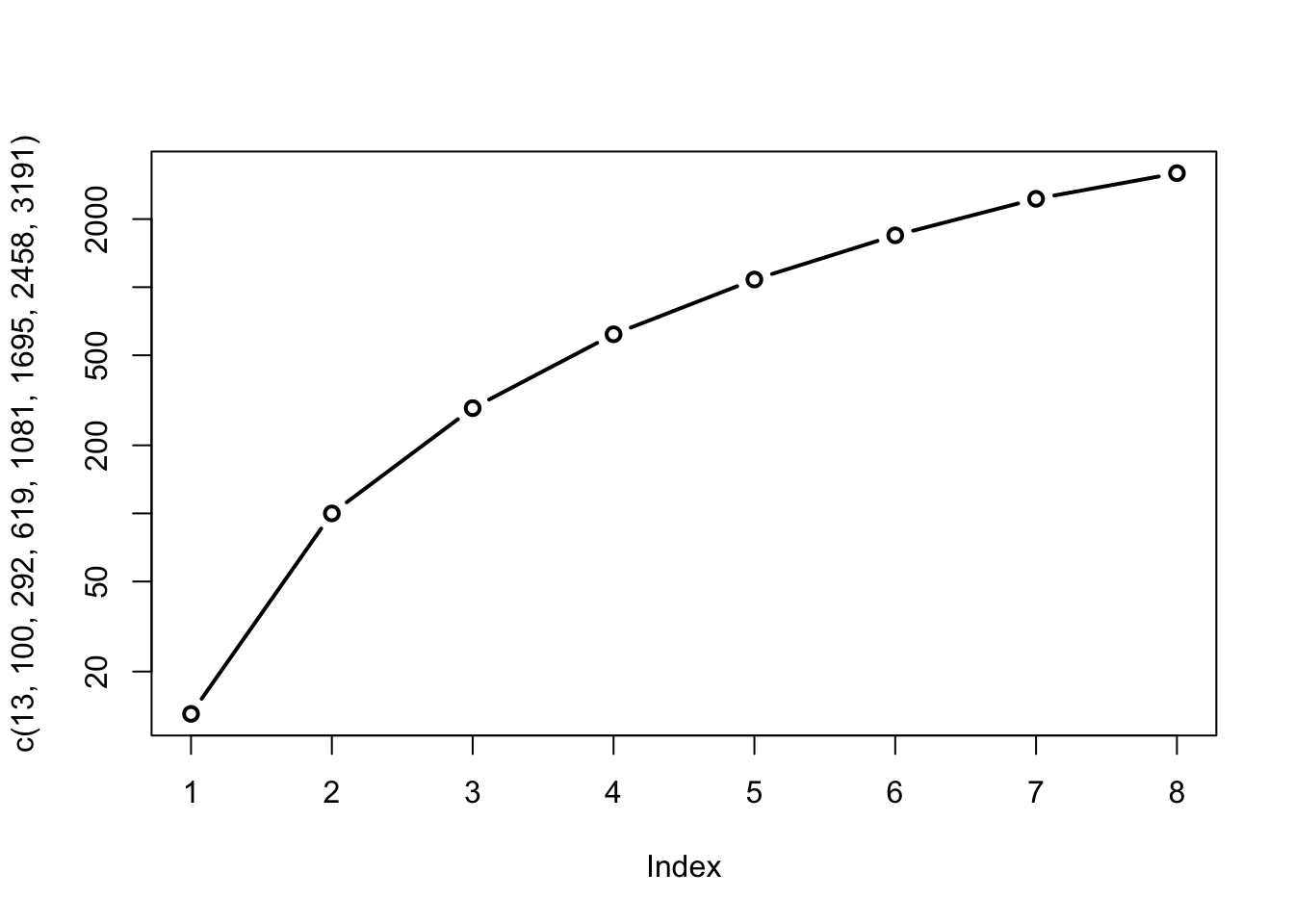
plot(N, type='l', log="y", col="seagreen", lwd=2)
In de eerste jaren neemt het aantal konijnen in een rechte lijn toe: de populatie groeit dus (bij benadering) exponentiëel. Later vlakt de groei af.
i. Doordat N[1] het aantal konijnen van tijdstap 0 bevat, moeten we dus kijken naar het 11e element uit de vector om het aantal konijnen na 10 jaar te weten.
N[11][1] 24575.4Het is vreemd dat het aantal konijnen geen geheel getal is. Blijkbaar bestaan er in dit wiskundige model ook halve konijnen. Later in de cursus gaan we hier dieper op in.
j.
# Stap 1: Stel begin-aantal konijnen in
N <- 24
b <- 3 # de birthrate is nu verhoogd naar 3
d <- 2e-9
# Stap 2: Verdubbel het aantal konijnen 30 keer
for (t in 1:30){
N[t+1] <- b*N[t] - d*N[t]^2
}
# Stap 3: Plot het resultaat
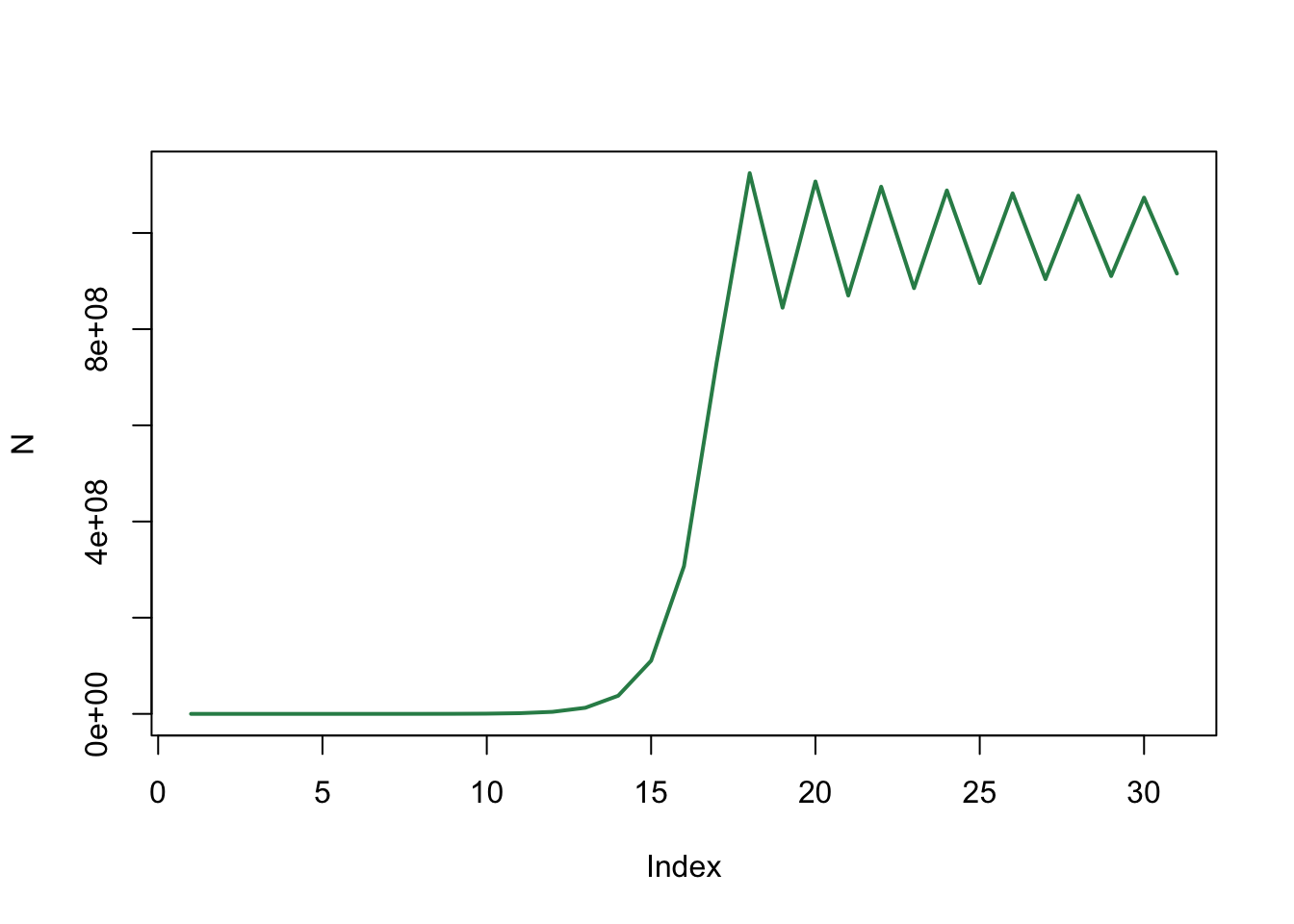
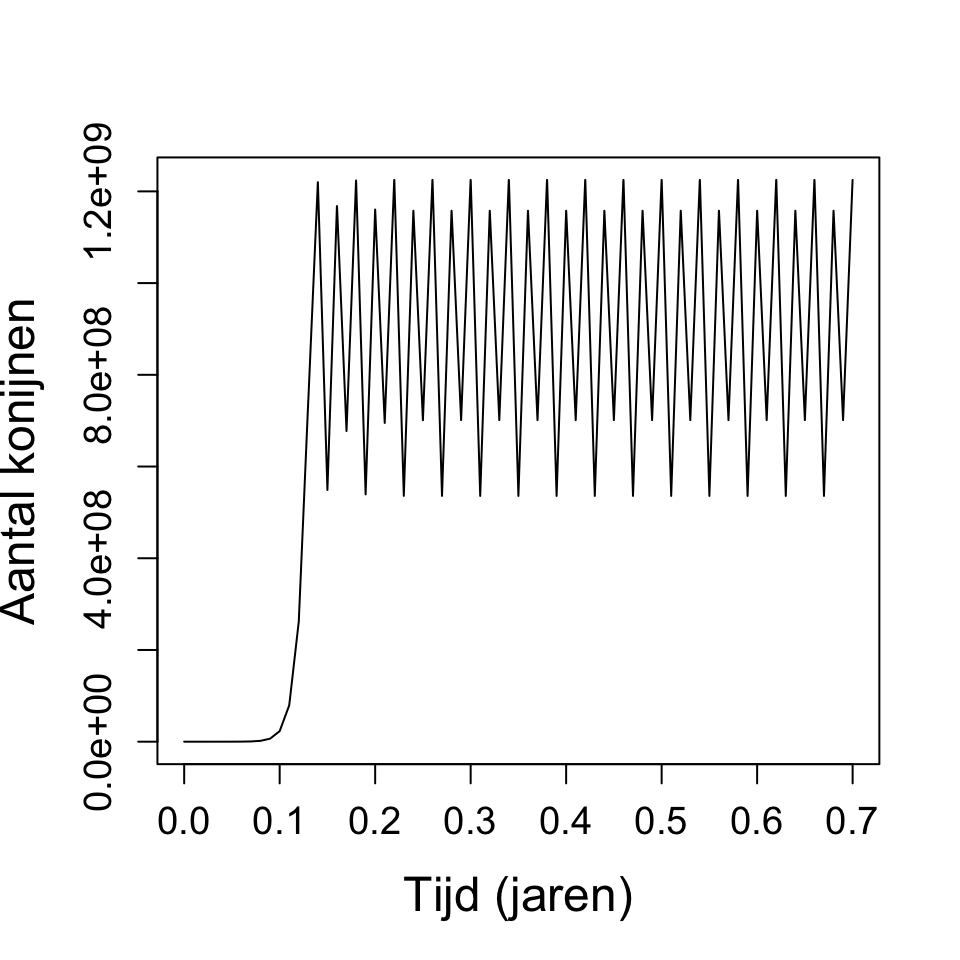
plot(N, type='l', col="seagreen", lwd=2)
We zien dat de konijnenpopulatie naar een ander evenwicht gaat, die ongeveer rond 1 miljard (1e+09) lijkt te liggen. Dit klopt met onze eerdere bepaling van de evenwichtwaarde: \(N_{evenwicht}=\frac{b-1}{d}=\frac{2}{2e-9} = 1e9\). Opvallend is dat de populatie een beetje rond deze waarde blijft schommelen.
k. Het lijkt erop dat we nog steeds geen 100 miljoen konijnen hebben na 10 jaar:
N[11][1] 1416507De groeisnelheid zal dus nog verder omhoog moeten.
l.
# Stap 1: Stel begin-aantal konijnen in
N <- 24
b <- 3.7 # de birthrate is nu verhoogd naar 3.7
d <- 2e-9
# Stap 2: Verdubbel het aantal konijnen 30 keer
for (t in 1:30){
N[t+1] <- b*N[t] - d*N[t]^2
}
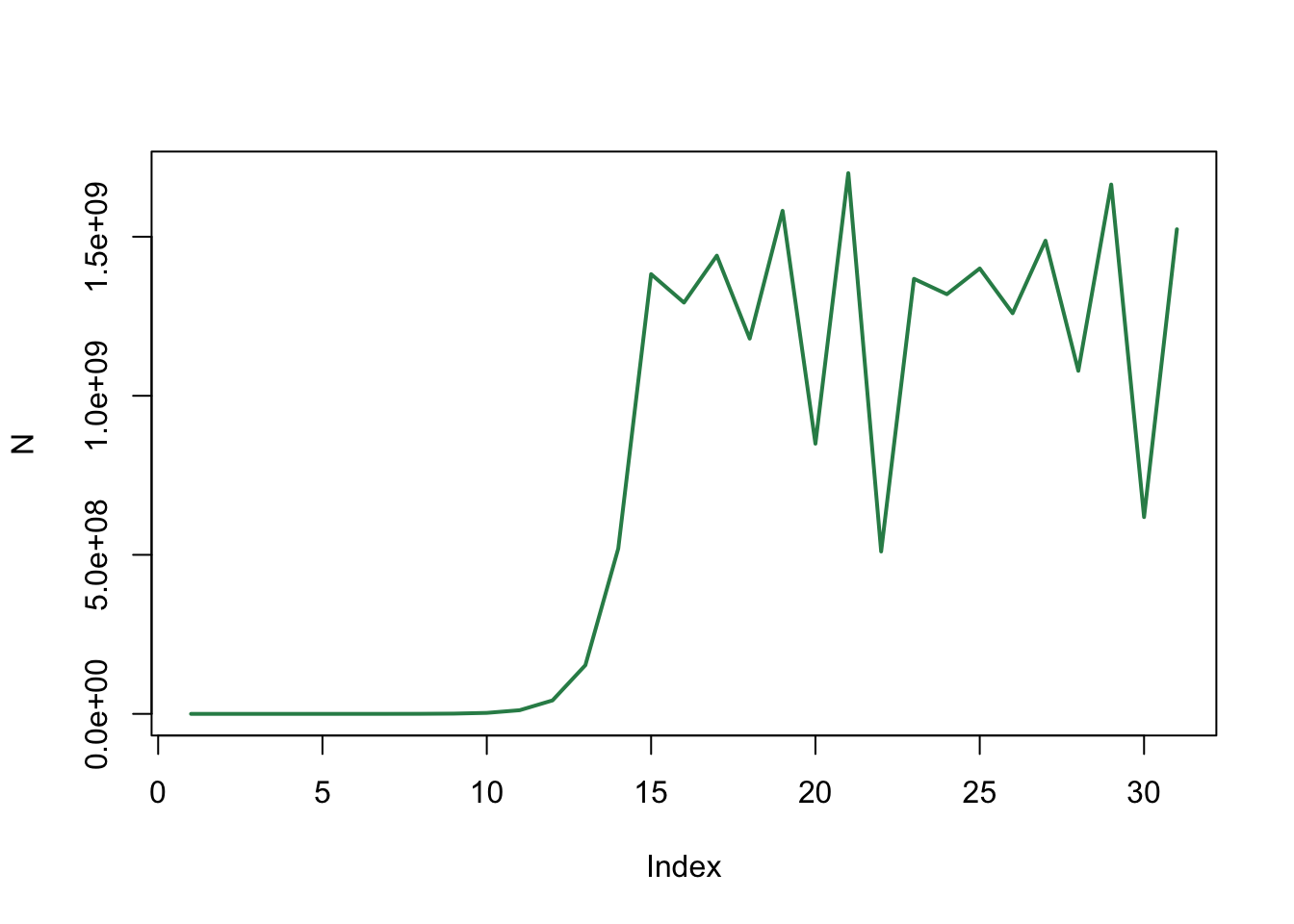
N[11][1] 11513965Het aantal konijnen komt dichter in de buurt: na 10 jaar hebben we 11.5 miljoen konijnen. Maar er lijkt wel iets vreemds te gebeuren met de populatie…
plot(N, type='l', col="seagreen", lwd=2)
Met \(b=3.7\) zien we dat de populatiegrootte blijft schommelen zo gauw hij in de buurt komt van de evenwichtswaarde. Het lukt niet meer om exact op de evenwichtswaarde te blijven, zoals wel het geval was in vraag h. Het lijkt wel of de populatiegrootte continu een beetje boven of onder de evenwichtswaarde uitkomt (hierover leer je in 11 Modelleren met ODEs meer!).
a. Er kunnen meerdere antwoorden goed zijn, want het gaat om je verwachting. Het belangrijkste van deze opdracht is dat je erover nadenkt wat je verwacht en waarom. Gebaseerd op de waarden van de parameters zou je verwachting kunnen zijn dat er wel exponentiële groei zal zijn, want b > d.
b. Er kunnen meerdere antwoorden goed zijn, want het gaat om je verwachting. Het belangrijkste van deze opdracht is dat je erover nadenkt wat je verwacht en waarom. De kans op een geboorte is voor elk individu 80%, en deze verandert niet met de populatiegrootte, dus je verwachting zou kunnen zijn dat er geen draagvermogen is. Een ander antwoord kan zijn dat je wel verwacht dat er een draagvermogen is, omdat er een eindig aantal vakjes is in het model.
c. In de simulatie kun je zien dat de populatie eerst erg snel groeit, en vervolgens stabiliseert. Er is dus wel een draagvermogen in dit model, ondanks dat we dit niet expliciet hebben gespecificeerd. Dat komt (zoals hierboven ook staat) doordat er in het model een beperkt aantal vakjes is waar konijnen in kunnen repliceren. Er kan in elk vakje maar één konijn zitten, dus als (bijna) alle vakjes al een konijn bevatten, kunnen er niet meer bij komen.
d. De toename is niet exponentieel. Dit kan je gemakkelijk zien op een log-lineaire schaal (soms in het kort ‘log-schaal’ genoemd):
plot(c(13,100,292,619,1081,1695,2458,3191), log="y", type = "b", lwd=2)
Bij een exponentiële toename zouden we een rechte lijn moeten zien wanneer we de y-as op logaritmische schaal plotten. Dat is hier duidelijk niet het geval.
e. Als één hokje een populatie konijnen voorstelt, zouden \(b\) en \(d\) geen geboorte en sterfte van individuen kunnen zijn. In plaats daarvan zou het over het uitbreiding of uitsterven van lokale konijnenpopulaties kunnen gaan.
Antwoorden 11 Modelleren met ODEs
a. De term \(k\) beschrijft het dumpen van plastic in de oceaan. \(k\) is een positieve term, het geeft dus een toename van de hoeveelheid plastic in de oceaan aan. Ook is het niet afhankelijk van de hoeveelheid plastic dat zich al in de oceaan bevindt. De term \(\delta P\) beschrijft de afbraak van plastic in de oceaan. Dit is een negatieve term, dus hierdoor neemt de hoeveelheid plastic in de oceaan af.
b. De eenheid van \(k\) is “kilo’s plastic per jaar”, want dit is ook de eenheid van \( \mathchoice{\frac{\mathrm{d}P} {\mathrm{d}t}}{\mathrm{d}P/\mathrm{d}t} {\mathrm{d}P/\mathrm{d}t} {\mathrm{d}P/\mathrm{d}t} \).
c. De eenheid van \(\delta\) is “per jaar”, want de term \(\delta P\) heeft de eenheid \(P \over t\) en \(\delta P = P \over t\) geeft \(\delta = {1 \over t}\).
d. De afbraak van plastic gaat erg langzaam, dus (met het huidige gedrag van mensen) is \(k\) veel groter dan \(\delta P\).
a. Bij \(P = {k \over \delta}\). Bij een evenwichtssituatie is \( \mathchoice{\frac{\mathrm{d}P} {\mathrm{d}t}}{\mathrm{d}P/\mathrm{d}t} {\mathrm{d}P/\mathrm{d}t} {\mathrm{d}P/\mathrm{d}t} \) gelijk aan nul. Dus:
\[\begin{align*} \mathchoice{\frac{\mathrm{d}P} {\mathrm{d}t}}{\mathrm{d}P/\mathrm{d}t} {\mathrm{d}P/\mathrm{d}t} {\mathrm{d}P/\mathrm{d}t} = k - \delta P = 0 \quad \text{ als...}\\ \delta P &= k & \\ P &= \frac{k}{\delta} & \end{align*}\]
b. Nee, want als er 0 plastic is (\(P = 0\)), is \( \mathchoice{\frac{\mathrm{d}P} {\mathrm{d}t}}{\mathrm{d}P/\mathrm{d}t} {\mathrm{d}P/\mathrm{d}t} {\mathrm{d}P/\mathrm{d}t} \) niet gelijk aan \(0\).
c. Zelfs als er geen plastic meer in de oceaan is, komt er altijd plastic bij (\(k\)), ook als \(P\) gelijk is aan nul. De hoeveelheid plastic in de oceaan zal dus gewoon weer toenemen. In het begin zal deze toename lineair zijn, want als er nog geen plastic in de oceaan is kan er ook niks afgebroken worden.
a. \[ \mathchoice{\frac{\mathrm{d}B} {\mathrm{d}t}}{\mathrm{d}B/\mathrm{d}t} {\mathrm{d}B/\mathrm{d}t} {\mathrm{d}B/\mathrm{d}t} = p - dB\]
b. De productiesnelheid \(p\) is al in de eenheid cellen per dag (net als \( \mathchoice{\frac{\mathrm{d}B} {\mathrm{d}t}}{\mathrm{d}B/\mathrm{d}t} {\mathrm{d}B/\mathrm{d}t} {\mathrm{d}B/\mathrm{d}t} \)) en hangt niet af van het aantal rode bloedcellen. Het aantal rode bloedcellen dat doodgaat hangt wel af van het aantal rode bloedcellen, dus dit is \(dB\). Dus \(d\) is heeft niet de eenheid “aantal cellen per dag”, maar de eenheid “per dag”.
c. Bij een evenwichtssituatie is \( \mathchoice{\frac{\mathrm{d}B} {\mathrm{d}t}}{\mathrm{d}B/\mathrm{d}t} {\mathrm{d}B/\mathrm{d}t} {\mathrm{d}B/\mathrm{d}t} \) gelijk aan nul. Dus:
\[\begin{align*} \mathchoice{\frac{\mathrm{d}B} {\mathrm{d}t}}{\mathrm{d}B/\mathrm{d}t} {\mathrm{d}B/\mathrm{d}t} {\mathrm{d}B/\mathrm{d}t} = p - d B = 0 \quad \text{ als...}\\ \delta B &= p & \\ B &= \frac{p}{d} & \end{align*}\]
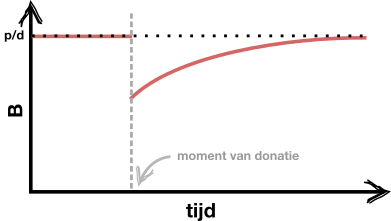
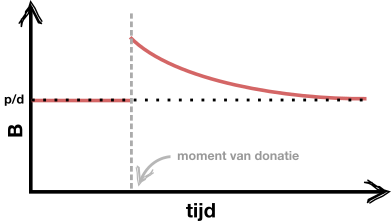
d.
Een goede schets ziet er ongeveer zo uit:
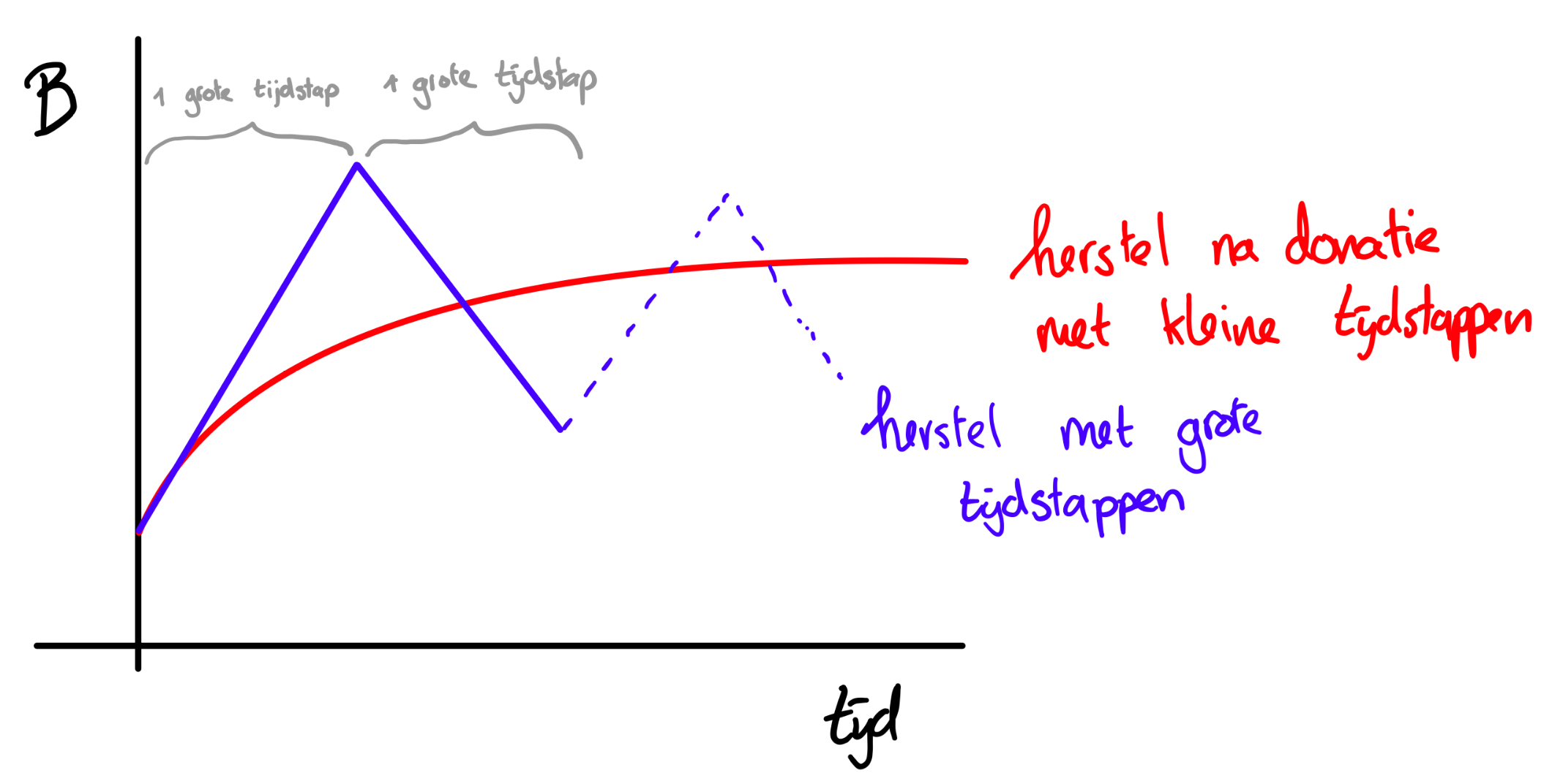
e.
Een goede schets ziet er ongeveer zo uit:
f. Het gaat hier om een intuitieve verwachting, dus er zijn ook andere verwachtingen mogelijk. Intuïtief zou je kunnen verwachten dat \(p\) bepaalt hoe snel je herstelt, omdat dit aangeeft hoeveel rode bloedcellen erbij komen.
Uitleg script In dit script kiezen we eerst waarden voor de parameters \(p\) en \(d\), en een beginwaarde voor \(B\). Daarna maken we een functie die \( \mathchoice{\frac{\mathrm{d}B} {\mathrm{d}t}}{\mathrm{d}B/\mathrm{d}t} {\mathrm{d}B/\mathrm{d}t} {\mathrm{d}B/\mathrm{d}t} \) uit kan rekenen voor verschillende waarden van \(B\), \(p\) en \(d\). Vervolgens maken we in stap 5 een vector \(B\) met de gewenste beginwaarde voor \(B\). In stap 6 rekenen we 500 keer uit wat de volgende waarde van \(B\) is. Dit is gelijk aan de vorige waarde van \(B\) plus de verandering \( \mathchoice{\frac{\mathrm{d}B} {\mathrm{d}t}}{\mathrm{d}B/\mathrm{d}t} {\mathrm{d}B/\mathrm{d}t} {\mathrm{d}B/\mathrm{d}t} \) voor die waarde van \(B\). Tot slot plotten we al deze waarden van \(B\) over de tijd, net zoals we in opdracht d en e deden. Let op dat minimale waarde op de y-as hier niet nul is, waardoor de plot er net iets anders uit ziet dan in d en e.
g.
Doordat \(B\) hier gelijk is aan de evenwichtswaarde is er geen verandering (\( \mathchoice{\frac{\mathrm{d}B} {\mathrm{d}t}}{\mathrm{d}B/\mathrm{d}t} {\mathrm{d}B/\mathrm{d}t} {\mathrm{d}B/\mathrm{d}t} = 0\)).
h. Te grote tijdstappen kunnen soms problemen geven, zoals we eerder in dit hoofdstuk al hebben gelezen. Dat komt doordat je de verandering per tijdstap uitrekent op basis van de huidige populatiegrootte. Dus als je net bloed hebt gedoneerd en op basis van het aantal rode bloedcellen nu wilt uitrekenen hoeveel rode bloedcellen je over één jaar hebt, dan zal dat veel te hoog uitvallen. Dat komt doordat het aantal rode bloedcellen meteen na een bloedtransfusie stijgt. Zoals je in de grafieken hierboven hebt gezien vlakt deze stijging na een tijdje echter af. Bij een te grote tijdstap kan het zo zijn dat je de aanvankelijke stijging “overschat”. Hierdoor kan je een situatie krijgen zoals in 10 Exponentiële groei waarbij er chaos ontstaat, doordat de populatiegrootte na één tijdstip boven of onder het evenwicht uitkomt.
i. Als je de code van g runt krijg je een grafiek te zien die helpt bij het beantwoorden van deze vraag.
# Stap 1: stel parameters in
p <- 2e11
d <- 1/120
# Stap 2: stel het beginaantal B in
B <- p/d
# Stap 3: maak functie die B, p, en d gebruikt om de verandering uit te rekenen
verandering <- function (B, p, d){
delta <- p - d*B
return(delta)
}
# Stap 4: een test of de functie werkt
# verandering(B=p/d, p=p, d=d)
# Stap 5: maak een lege lijst met begin-aantal erin
B <- c(0.9*p/d)
# Stap 6: reken 500 keer de volgende hoeveelheid B uit
for (t in 1:500) {
B[t+1] <- B[t] + verandering(B=B[t], p=p, d=d)
}
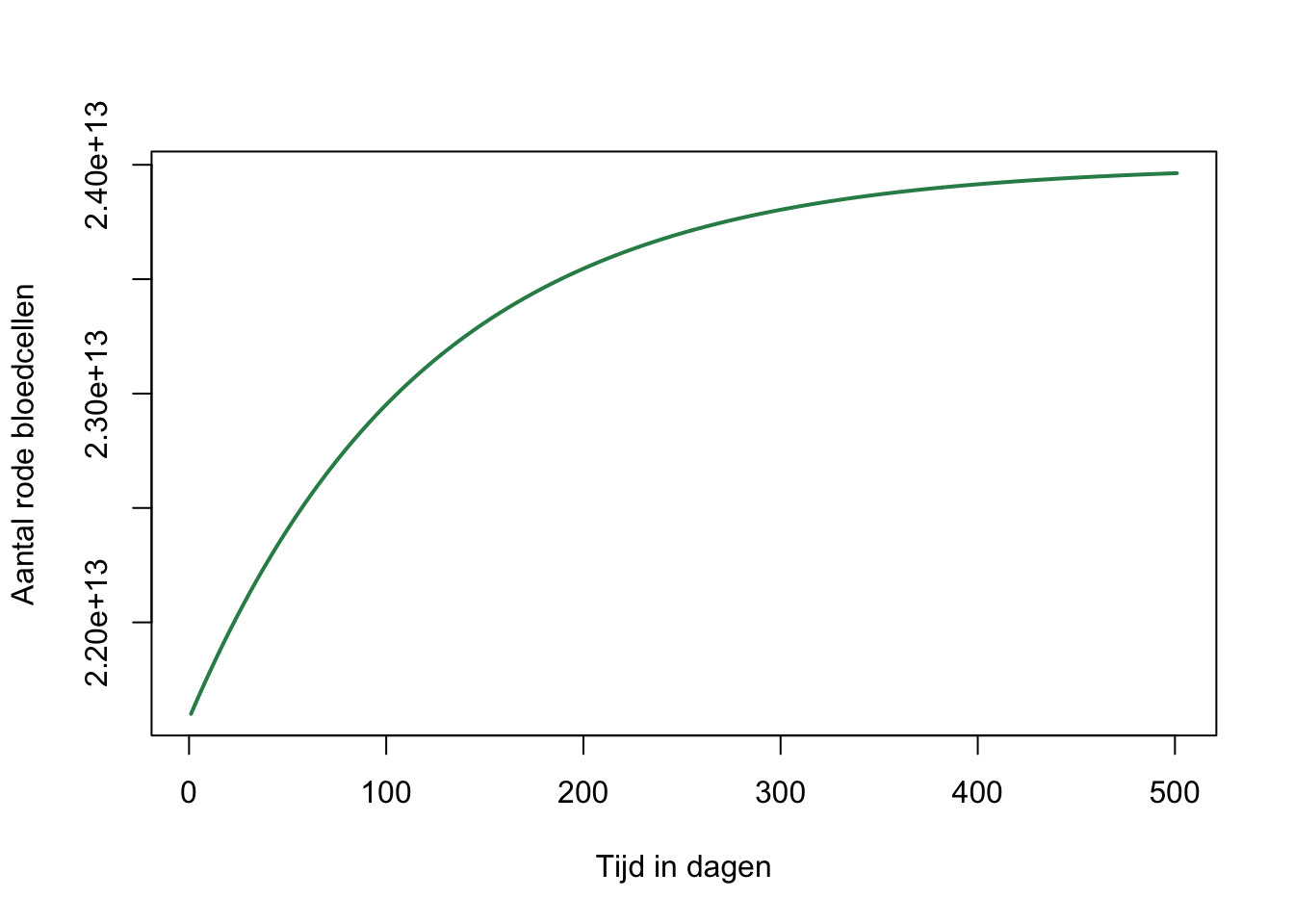
# Stap 7: plot de tijdserie
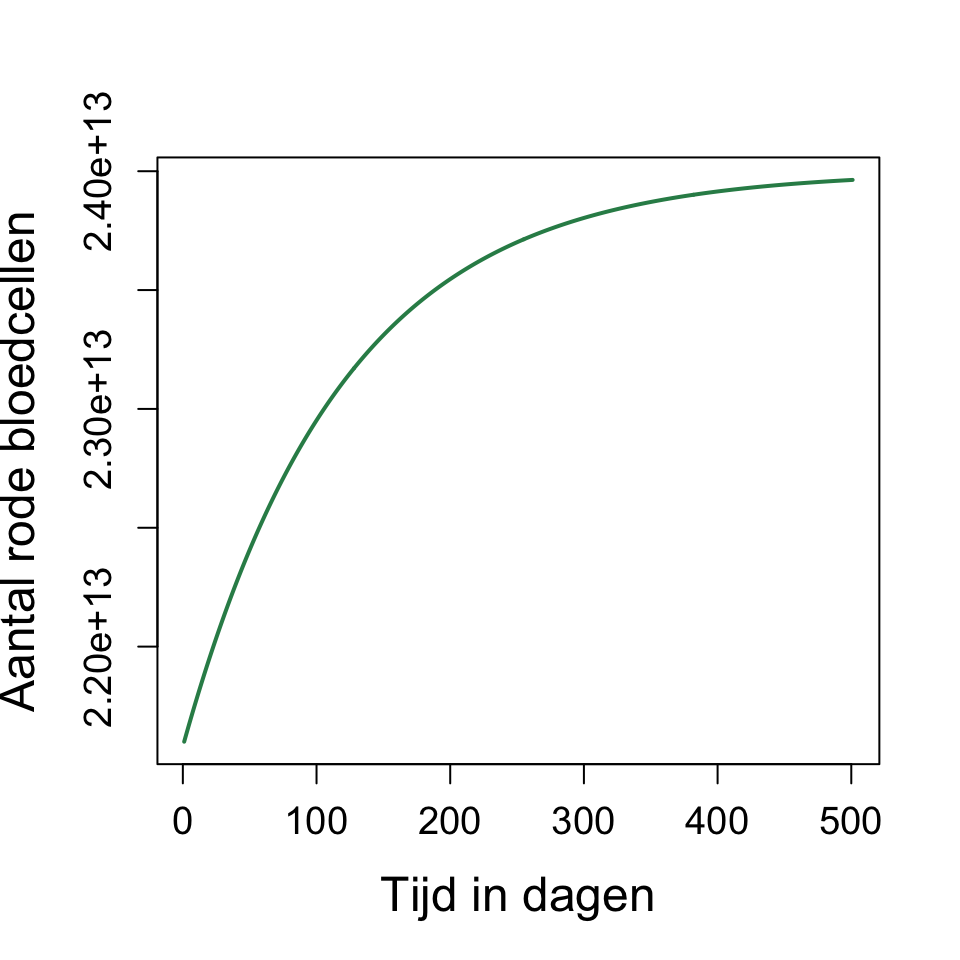
plot(B, xlab="Tijd in dagen", ylab="Aantal rode bloedcellen", type="l", col="seagreen", lwd=2)
Hieruit kunnen we aflezen dat de helft van het bloedverlies na ongeveer 100 dagen weer hersteld is. Hierom moet je tussen donaties altijd 3 tot 4 maanden wachten.
j.
Dit is een kleine aanpassing in de code:
# Stap 1: stel parameters in
p <- 2e11
d <- 1/120
# Stap 2: stel het beginaantal B in
B <- p/d
# Stap 3: maak functie die B, p, en d gebruikt om de verandering uit te rekenen
verandering <- function (B, p, d){
delta <- p - d*B
return(delta)
}
# Stap 4: een test of de functie werkt
# verandering(B=p/d, p=p, d=d)
# Stap 5: maak een lege lijst met begin-aantal erin, waarbij we slechts 0.1% bloed doneren
B <- c(0.999*p/d)
# Stap 6: reken 500 keer de volgende hoeveelheid B uit
for (t in 1:500) {
B[t+1] <- B[t] + verandering(B=B[t], p=p, d=d)
}
# Stap 7: plot de tijdserie
plot(B, xlab="Tijd in dagen", ylab="Aantal rode bloedcellen", type="l",
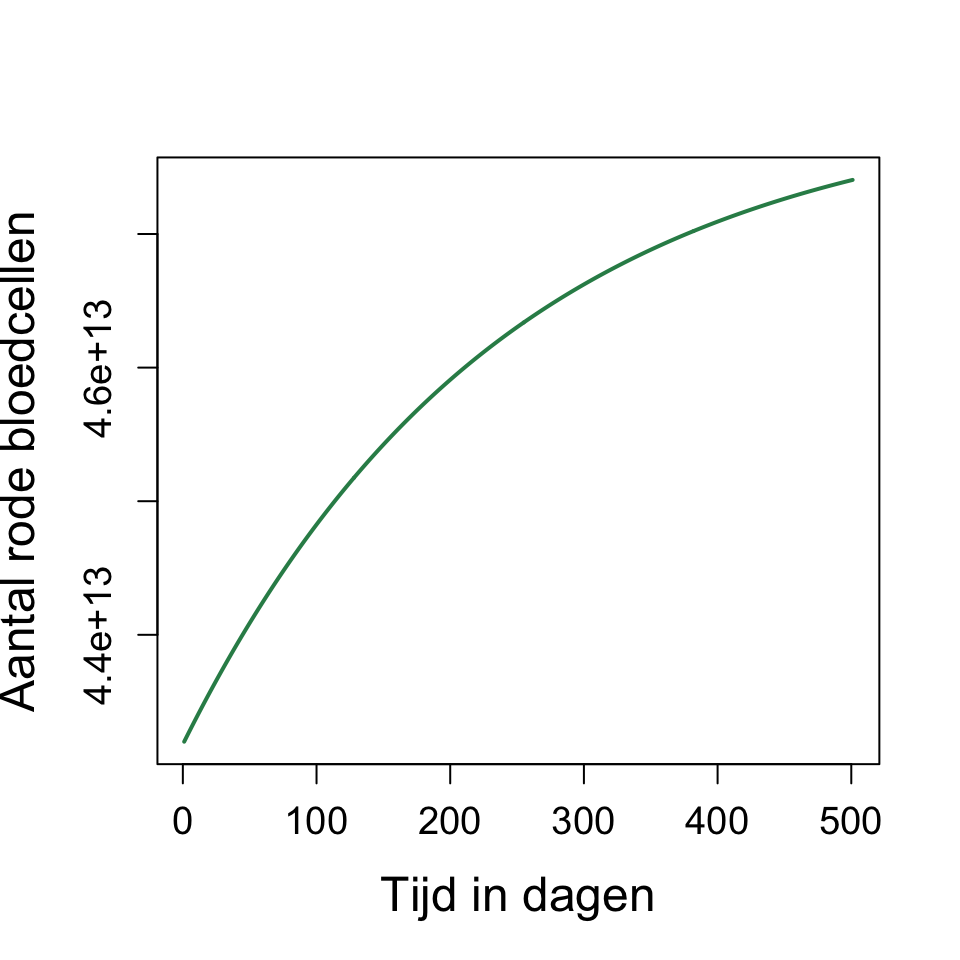
col="seagreen", lwd=2)
Het duurt nog steeds even lang om van de helft van het bloedverlies te herstellen! De helft is nu wel veel minder (dus er is in totaal minder te herstellen), maar het herstel gaat nog steeds even snel.
k. Het gaat hier wederom om een verwachting, dus er zijn geen foute antwoorden! Intuïtief zou je kunnen verwachten dat \(p\) bepaalt hoe snel je herstelt, omdat dit aangeeft hoeveel rode bloedcellen erbij komen.
l. Je kunt het script uit de opdracht gebruiken en de waarden voor \(p\) en \(d\) aanpassen om te kijken hoe dit de snelheid van het herstel beïnvloedt.
# Originele parameterwaarden
# Stap 1: stel parameters in
p <- 2e11
d <- 1/120
# Stap 2: stel het beginaantal B in
B <- p/d
# Stap 3: maak functie die B, p, en d gebruikt om de verandering uit te rekenen
verandering <- function (B, p, d){
delta <- p - d*B
return(delta)
}
# Stap 4: een test of de functie werkt
# verandering(B=p/d, p=p, d=d)
# Stap 5: maak een lege lijst met begin-aantal erin
B <- c(0.9*p/d)
# Stap 6: reken 500 keer de volgende hoeveelheid B uit
for (t in 1:500) {
B[t+1] <- B[t] + verandering(B=B[t], p=p, d=d)
}
# Stap 7: plot de tijdserie
plot(B, xlab="Tijd in dagen", ylab="Aantal rode bloedcellen", type="l",
col="seagreen", lwd=2, cex.lab=1.5, cex.axis=1.2)
# Grotere waarde voor p (snellere productie)
# Stap 1: stel parameters in
p <- 2e12 # verhoog p
d <- 1/120 # houdt d op de oude waarde
# Stap 2-4 blijft hetzelfde en kunnen we overslaan
# Stap 5: maak een lege lijst met begin-aantal erin
B <- c(0.9*p/d)
# Stap 6: reken 500 keer de volgende hoeveelheid B uit
for (t in 1:500) {
B[t+1] <- B[t] + verandering(B=B[t], p=p, d=d)
}
# Stap 7: plot de tijdserie
plot(B, xlab="Tijd in dagen", ylab="Aantal rode bloedcellen", type="l",
col="seagreen", lwd=2, cex.lab=1.5, cex.axis=1.2)
# Kleinere waarde voor d (minder sterfte)
# Stap 1: stel parameters in
p <- 2e11 # zet p terug naar de oude waarde
d <- 1/240 # verlaag d
# Stap 2-4 blijft hetzelfde en kunnen we overslaan
# Stap 5: maak een lege lijst met begin-aantal erin
B <- c(0.9*p/d)
# Stap 6: reken 500 keer de volgende hoeveelheid B uit
for (t in 1:500) {
B[t+1] <- B[t] + verandering(B=B[t], p=p, d=d)
}
# Stap 7: plot de tijdserie
plot(B, xlab="Tijd in dagen", ylab="Aantal rode bloedcellen", type="l",
col="seagreen", lwd=2, cex.lab=1.5, cex.axis=1.2)
De snelheid van het herstel verandert niet als we \(p\) veranderen. Deze verandert echter wel als we \(d\) veranderen. Wellicht tegen je biologische intuïtie in, bepaalt \(d\) dus de snelheid van het herstel!
a. Met \(r < 1\) gaat de populatie uiteindelijk altijd naar nul.
Vanaf \(r > 3\) ontstaan er fluctuaties rondom het evenwicht.
Met \(r > 3.7\) ontstaat er chaos.
Code
# R = 0.8
# Stap 1, definieer beginaantal konijnen en parameters
N <- 24 # aantal konijnen
r <- 0.8 # intrinsieke groeisnelheid
K <- 10^9 # schaalt de dichtheidsafhankelijkheid
# Stap 2: bereken het aantal konijnen in [t+1] 40 keer
for (t in 1:40){
N[t+1] <- r*N[t]*(1-(N[t]/K))
}
# Stap 3: bekijk resultaten
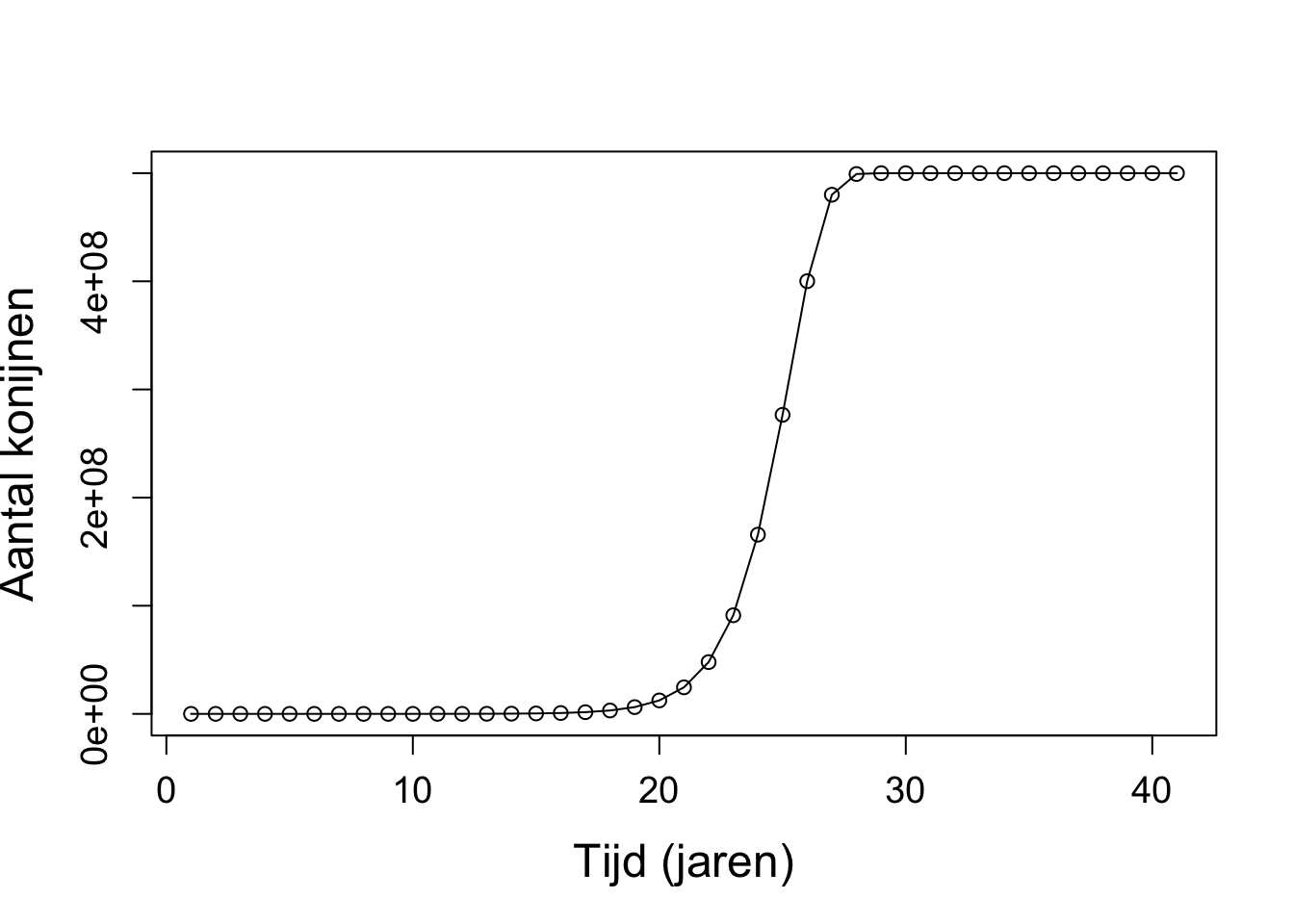
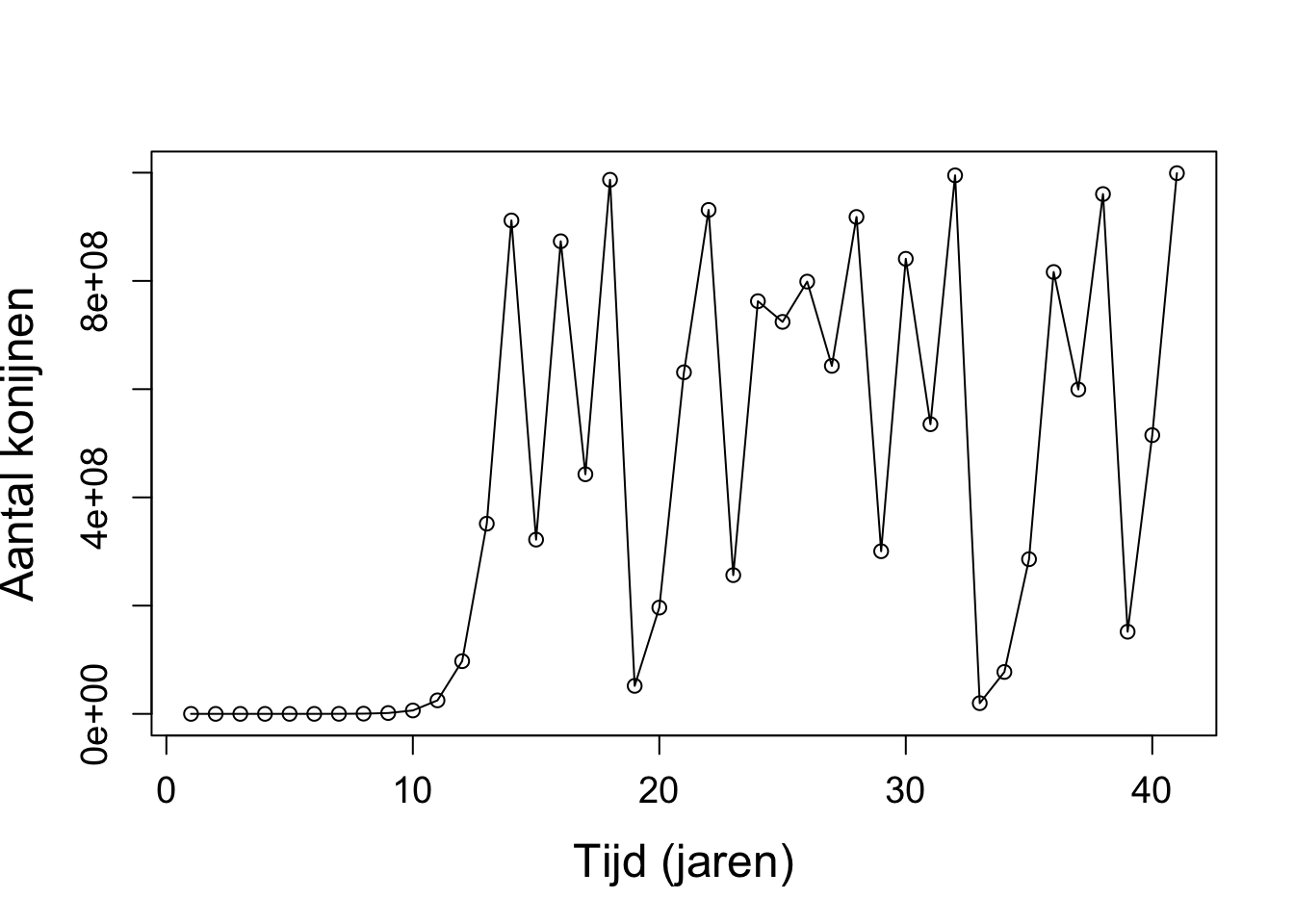
plot(N,type="o",xlab="Tijd (jaren)", ylab="Aantal konijnen",
cex.lab=1.5, cex.axis=1.2)
# R = 2
# Stap 1, definieer beginaantal konijnen en parameters
N <- 24 # aantal konijnen
r <- 2 # intrinsieke groeisnelheid
K <- 10^9 # schaalt de dichtheidsafhankelijkheid
# Stap 2: bereken het aantal konijnen in [t+1] 40 keer
for (t in 1:40){
N[t+1] <- r*N[t]*(1-(N[t]/K))
}
# Stap 3: bekijk resultaten
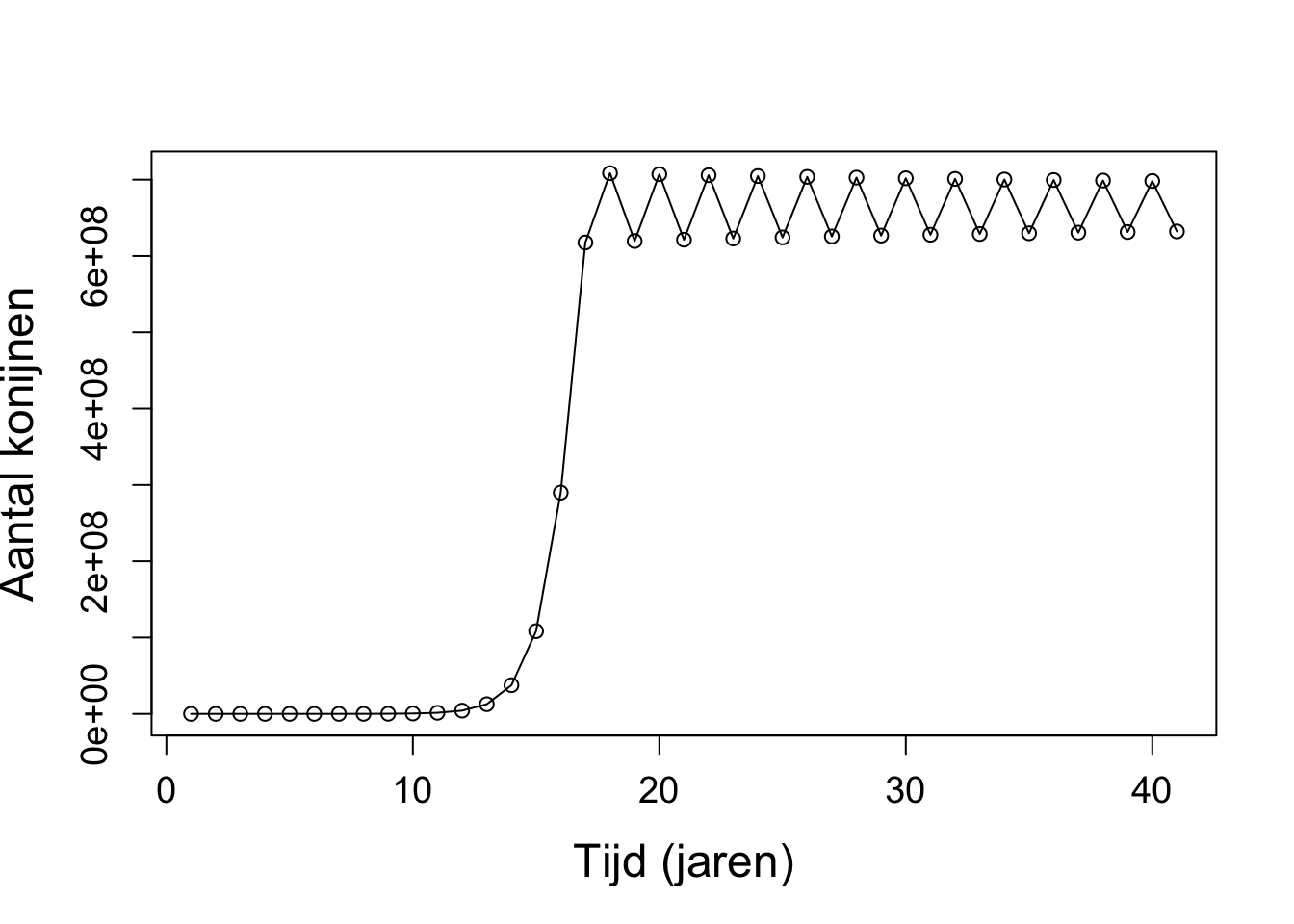
plot(N,type="o",xlab="Tijd (jaren)", ylab="Aantal konijnen",
cex.lab=1.5, cex.axis=1.2)
# R = 3
# Stap 1, definieer beginaantal konijnen en parameters
N <- 24 # aantal konijnen
r <- 3 # intrinsieke groeisnelheid
K <- 10^9 # schaalt de dichtheidsafhankelijkheid
# Stap 2: bereken het aantal konijnen in [t+1] 40 keer
for (t in 1:40){
N[t+1] <- r*N[t]*(1-(N[t]/K))
}
# Stap 3: bekijk resultaten
plot(N,type="o",xlab="Tijd (jaren)", ylab="Aantal konijnen",
cex.lab=1.5, cex.axis=1.2)
# R = 4
# Stap 1, definieer beginaantal konijnen en parameters
N <- 24 # aantal konijnen
r <- 4 # intrinsieke groeisnelheid
K <- 10^9 # schaalt de dichtheidsafhankelijkheid
# Stap 2: bereken het aantal konijnen in [t+1] 40 keer
for (t in 1:40){
N[t+1] <- r*N[t]*(1-(N[t]/K))
}
# Stap 3: bekijk resultaten
plot(N,type="o",xlab="Tijd (jaren)", ylab="Aantal konijnen",
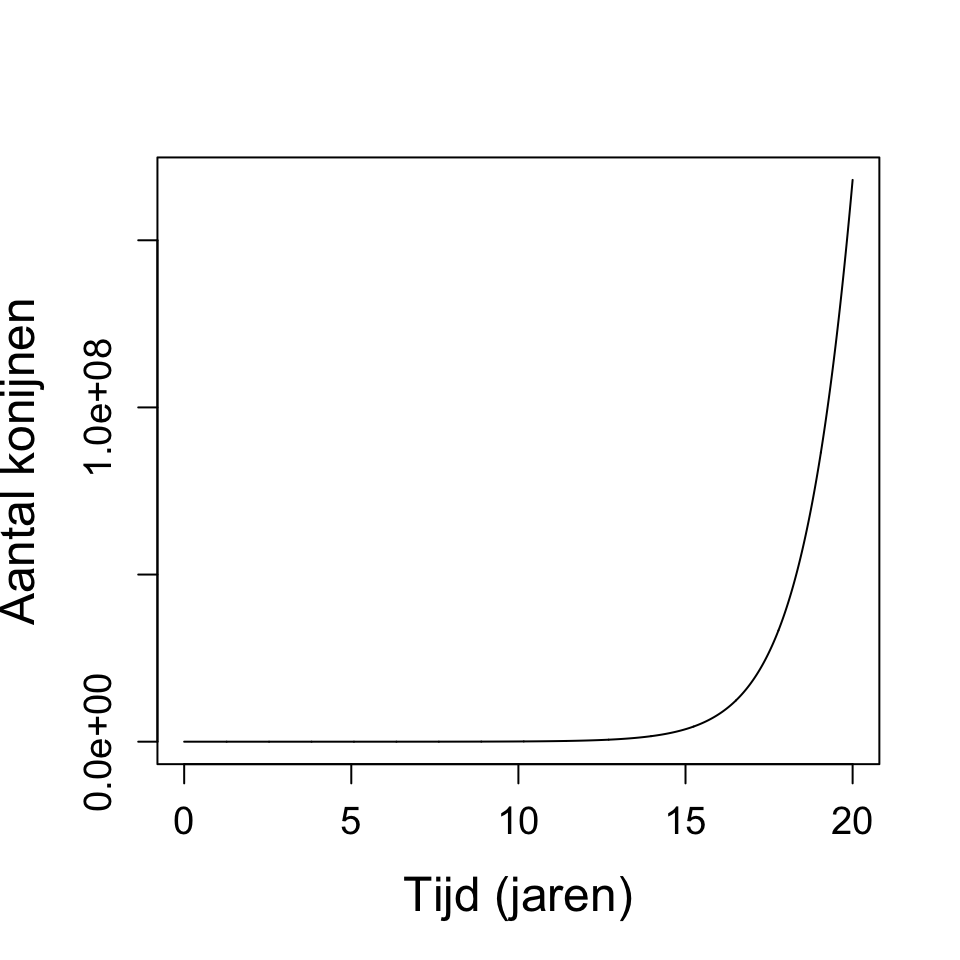
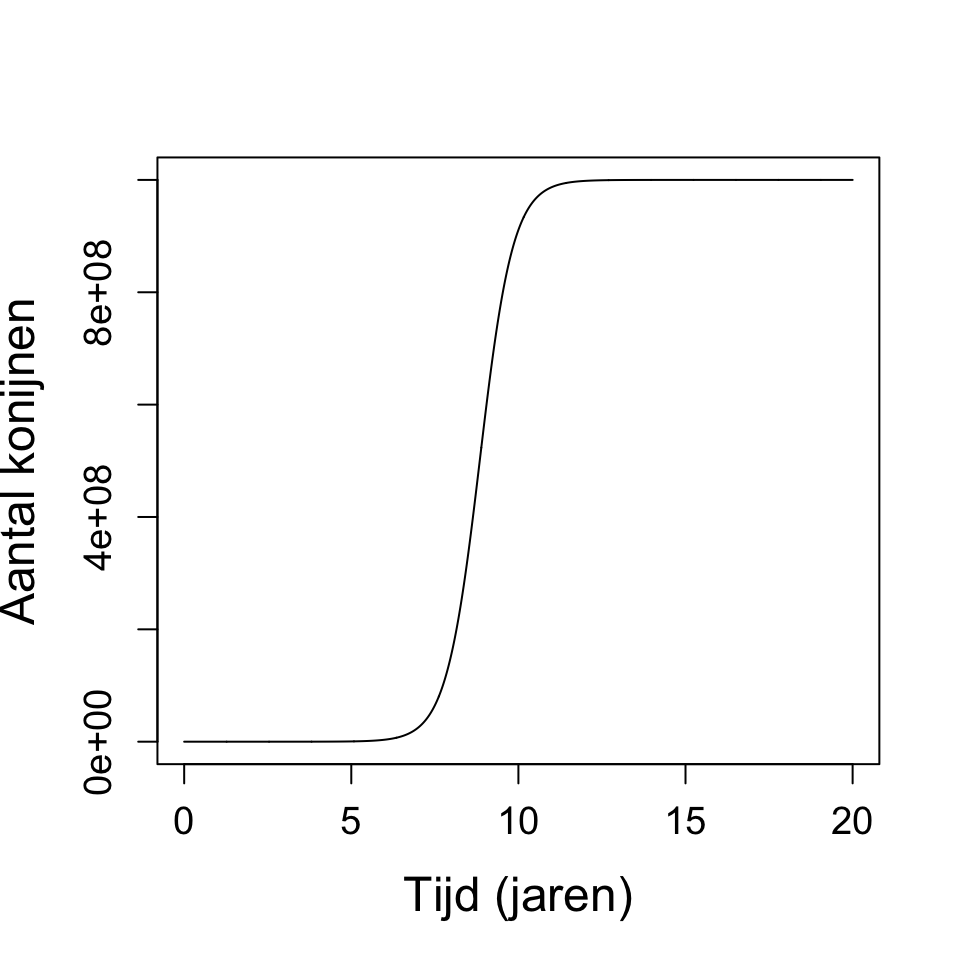
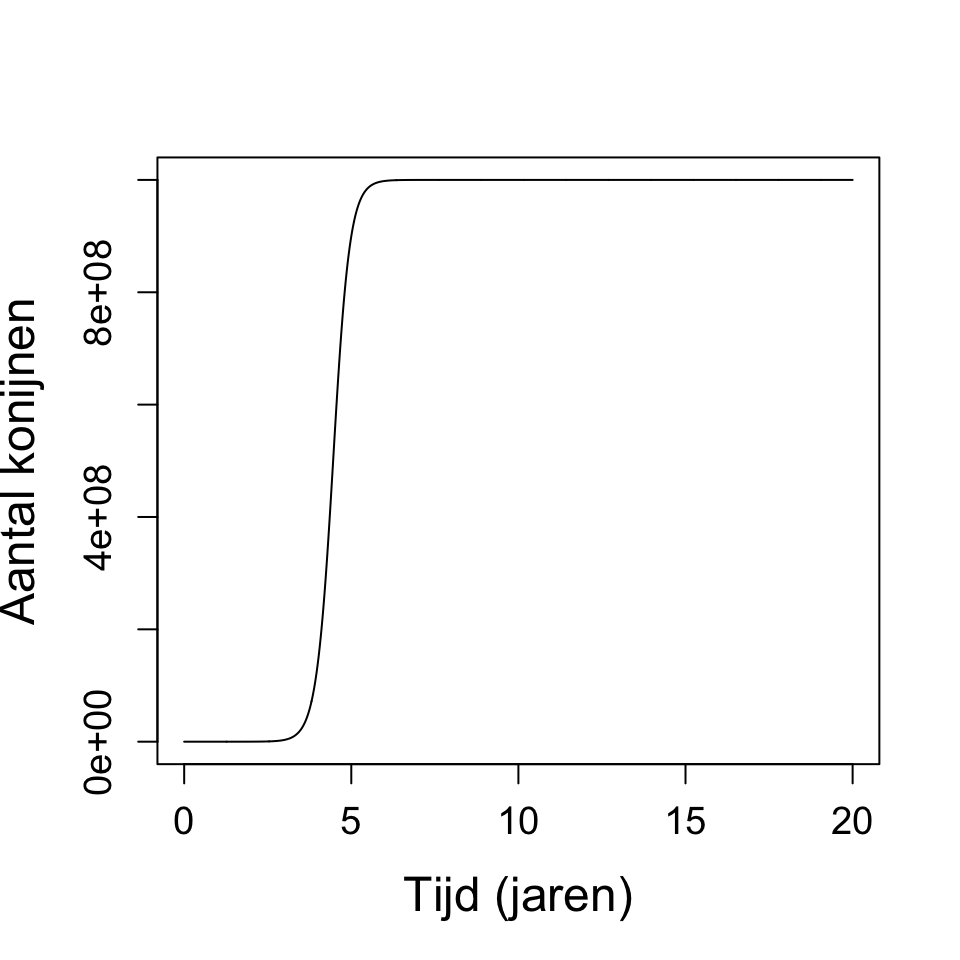
cex.lab=1.5, cex.axis=1.2)
b. In tegenstelling tot de differentievergelijking, geeft de differentiaalvergelijking ook groei wanneer \(r < 1\). Daarnaast geeft \(r > 3.7\) geen chaos, waar dat bij de differentievergelijking wel was. Om chaos te krijgen in dit model moet je \(r\) heel erg groot maken, bijvoorbeeld bij \(r = 250\) krijg je wel fluctuaties.
Code
# r = 0.8
# SIMPEL SCRIPT VOOR DIFFERENTIAALVERGELIJKING
# Stap 1, definieer beginaantal konijnen en parameters
N <- 24
r <- 0.8
K <- 10^9
# Stap 2, definieer tijdstappen en maak een dataframe aan
delta_t <- 0.01 # grootte van de tijdstap
tijdstapjes <- seq(0,20,by=delta_t)
tijdserie <- data.frame(t=tijdstapjes,konijnen=N)
# Stap 3: Reken in kleine stapjes de volgende N uit
for (t in 1:length(tijdstapjes)-1){
groeiN <- delta_t * r*N*(1-N/K)
N <- N + groeiN
tijdserie[t+1,"konijnen"] <- N
}
# Stap 3: bekijk resultaten
plot(tijdserie$t, tijdserie$konijnen, type="l",xlab="Tijd (jaren)",
ylab="Aantal konijnen", cex.lab=1.5, cex.axis=1.2)
# r = 2
# SIMPEL SCRIPT VOOR DIFFERENTIAALVERGELIJKING
# Stap 1, definieer beginaantal konijnen en parameters
N <- 24
r <- 2
K <- 10^9
# Stap 2, definieer tijdstappen en maak een dataframe aan
delta_t <- 0.01 # grootte van de tijdstap
tijdstapjes <- seq(0,20,by=delta_t)
tijdserie <- data.frame(t=tijdstapjes,konijnen=N)
# Stap 3: Reken in kleine stapjes de volgende N uit
for (t in 1:length(tijdstapjes)-1){
groeiN <- delta_t * r*N*(1-N/K)
N <- N + groeiN
tijdserie[t+1,"konijnen"] <- N
}
# Stap 3: bekijk resultaten
plot(tijdserie$t, tijdserie$konijnen, type="l",xlab="Tijd (jaren)",
ylab="Aantal konijnen", cex.lab=1.5, cex.axis=1.2)
# r = 4
# SIMPEL SCRIPT VOOR DIFFERENTIAALVERGELIJKING
# Stap 1, definieer beginaantal konijnen en parameters
N <- 24
r <- 4
K <- 10^9
# Stap 2, definieer tijdstappen en maak een dataframe aan
delta_t <- 0.01 # grootte van de tijdstap
tijdstapjes <- seq(0,20,by=delta_t)
tijdserie <- data.frame(t=tijdstapjes,konijnen=N)
# Stap 3: Reken in kleine stapjes de volgende N uit
for (t in 1:length(tijdstapjes)-1){
groeiN <- delta_t * r*N*(1-N/K)
N <- N + groeiN
tijdserie[t+1,"konijnen"] <- N
}
# Stap 3: bekijk resultaten
plot(tijdserie$t, tijdserie$konijnen, type="l",xlab="Tijd (jaren)",
ylab="Aantal konijnen", cex.lab=1.5, cex.axis=1.2)
# r = 250
# SIMPEL SCRIPT VOOR DIFFERENTIAALVERGELIJKING
# Stap 1, definieer beginaantal konijnen en parameters
N <- 24
r <- 250
K <- 10^9
# Stap 2, definieer tijdstappen en maak een dataframe aan
delta_t <- 0.01 # grootte van de tijdstap
tijdstapjes <- seq(0,0.7,by=delta_t)
tijdserie <- data.frame(t=tijdstapjes,konijnen=N)
# Stap 3: Reken in kleine stapjes de volgende N uit
for (t in 1:length(tijdstapjes)-1){
groeiN <- delta_t * r*N*(1-N/K)
N <- N + groeiN
tijdserie[t+1,"konijnen"] <- N
}
# Stap 3: bekijk resultaten
plot(tijdserie$t, tijdserie$konijnen, type="l",xlab="Tijd (jaren)",
ylab="Aantal konijnen", cex.lab=1.5, cex.axis=1.2)
c. Het script wordt dan heel erg langzaam. ODEs zijn dus precieser, maar dat wordt ook steeds moeilijker voor je computer. Dit is waarom je meestal betere tools gebruikt om ODEs te integreren, zoals Grind (dit R-script zul je later in de cursus zien).
# SIMPEL SCRIPT VOOR DIFFERENTIAALVERGELIJKING
# Stap 1, definieer beginaantal konijnen en parameters
N <- 24
r <- 2
K <- 10^9
# Stap 2, definieer tijdstappen en maak een dataframe aan
delta_t <- 0.0001 # grootte van de tijdstap
tijdstapjes <- seq(0,20,by=delta_t)
tijdserie <- data.frame(t=tijdstapjes,konijnen=N)
# Stap 3: Reken in kleine stapjes de volgende N uit
for (t in 1:length(tijdstapjes)-1){
groeiN <- delta_t * r*N*(1-N/K)
N <- N + groeiN
tijdserie[t+1,"konijnen"] <- N
}
# Stap 3: bekijk resultaten
tijdserie[20,] # Aantal na 0.19 jaar
plot(tijdserie$t, tijdserie$konijnen, type="l",xlab="Tijd (jaren)", ylab="Aantal konijnen")Antwoorden 12 Dichtheidseffecten
a. Als we de birth (\(b\)) vermenigvuldigen met de functionele respons \(\frac{N}{K} + 1\), zal dit birth juist verhogen omdat \(N\) een positieve term is. Als de populatie (\(N\)) heel klein is, is de functie gelijk aan 1 en is de uiteindelijke (minimale) birth dus gelijk aan \(b\). Als \(N\) heel groot is, neemt de birth alsmaar toe! (biologisch gezien is dit natuurlijk vreemd!)
b. Als we de birth (\(b\)) vermenigvuldigen met de functionele respons \(1-cN\), zal er een zeer vergelijkbaar effect zijn als met \(f(N)=1-\frac NK\) (zoals gebruikt in het hoofdstuk). Het enige verschil is dat we het negatieve effect niet delen door \(K\), maar vermenigvuldigen met \(c\). Maar, als \({1 \over K}=c\), dan staat er precies hetzelfde! We hebben dus wederom een maximale geboorte voor kleine populaties (kleine \(N\)).
c. Als we de birth (\(b\)) vermenigvuldigen met de functionele respons \(1-cN^2\), zien we dat de birth rate zal afnemen met toenemende populatiegrootte. Echter is deze respons niet lineair, maar kwadratisch. De maximale birth rate is dus nogsteeds gelijk aan \(b\) (wanneer \(N\) klein is), voor kleine populaties zal de birth slechts langzaam afnemen (want kleine getallen kwadrateren geeft extra kleine getallen), maar voor grote populaties zal birth juist heel snel afnemen!
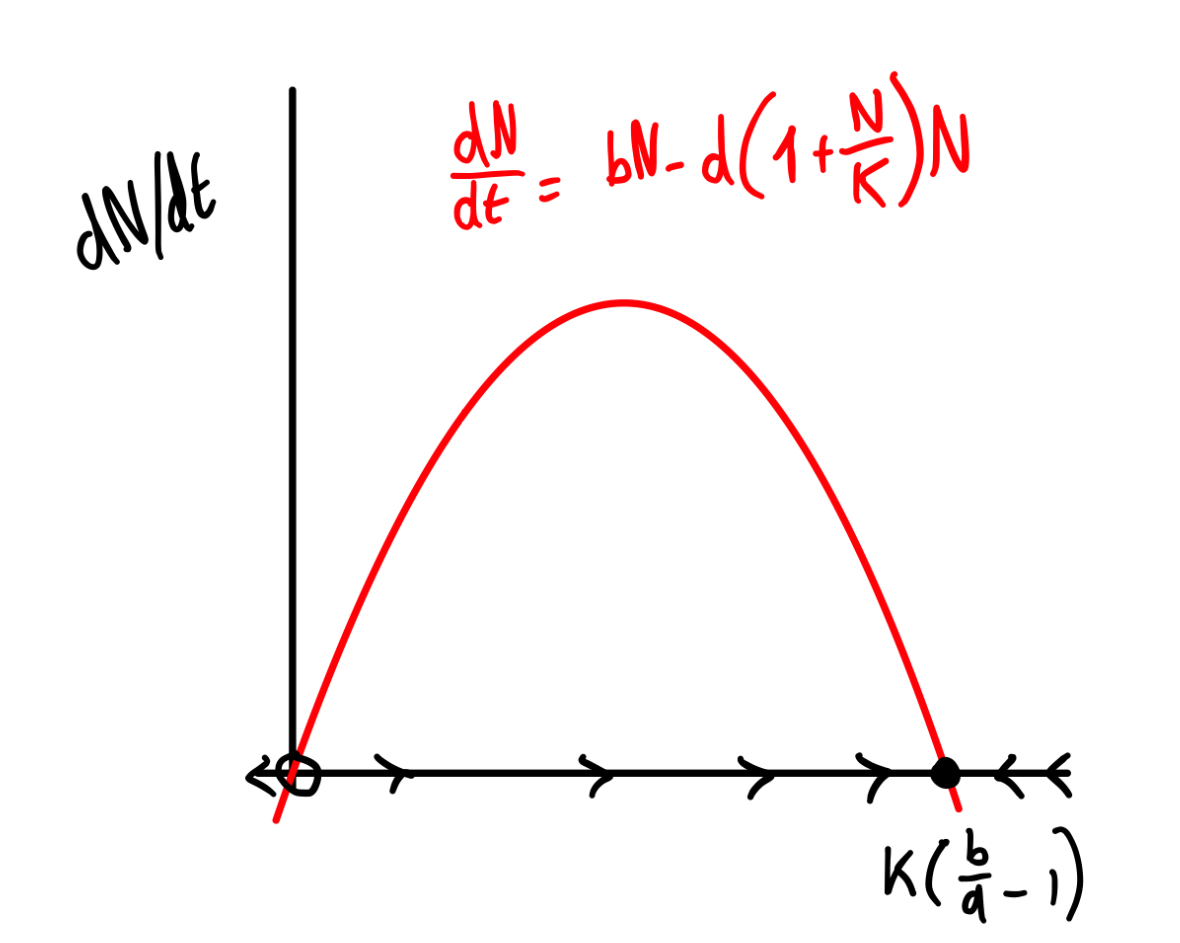
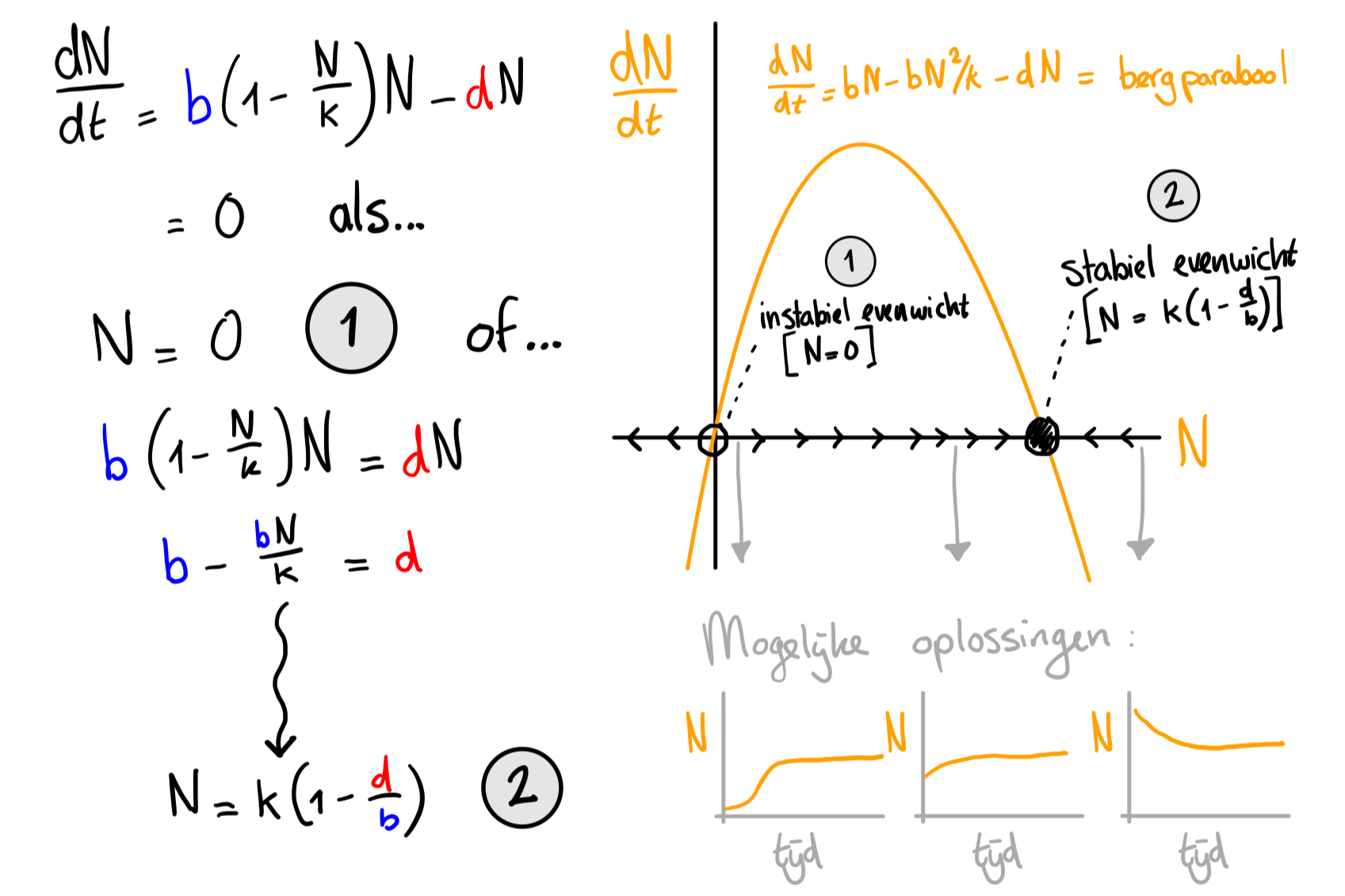
a. Er is een evenwicht als: \[\begin{align*} \mathchoice{\frac{\mathrm{d}N} {\mathrm{d}t}}{\mathrm{d}N/\mathrm{d}t} {\mathrm{d}N/\mathrm{d}t} {\mathrm{d}N/\mathrm{d}t} &= 0 \\ bN-d\left(1+\frac NK \right)N &= 0 \\ N &= 0 \quad \text{(oplossing 1)} \\ b-d\left(1+\frac NK \right) &= 0 \\ d\left(1+\frac NK \right) &= b \\ \left(1+\frac NK \right) &= b/d \\ \frac{N}{K} &= b/d - 1\\ N &= K(b/d -1) \quad \text{(oplossing 2)} \\ \end{align*}\]
b. Net zoals in Figuur 12.2 hebben we weer een bergparabool vanwege de term \(-d\left(1+\frac NK \right)N = -dN - \frac{d}{K} N^2\)
We hebben de twee evenwichten berekend in vraag a: \(N=0\) en \(N=K\left( \frac bd - 1 \right)\). Het triviale evenwicht \(N=0\) is geen attractor, het andere evenwicht wel.
a. De term \(rB\) is de exponentiële groei van de bacteriën. De term \(kNB\) beschrijft het aantal bacteriën dat door neutrofielen wordt doodgemaakt. De eenheden van beide termen zijn in bacteriën per uur.
b. \(rB\) en \(kNB\) moeten allebei de eenheid aantal bacteriën per uur hebben, omdat we ze bij elkaar optellen om \( \mathchoice{\frac{\mathrm{d}N} {\mathrm{d}t}}{\mathrm{d}N/\mathrm{d}t} {\mathrm{d}N/\mathrm{d}t} {\mathrm{d}N/\mathrm{d}t} \) te krijgen.
\(B\) heeft de eenheid bacteriën, dus \(r\) moet de eenheid per uur (\(uur^{-1}\)) hebben, zodat de term \(rB\) als geheel de eenheid bacteriën per uur heeft.
\(N\) heeft de eenheid hoeveelheid neutrofielen, dus k moet dit wegdelen. We hebben dus: \[\frac{aantal \, \, bacterien}{uur} = k \cdot aantal \, \, neutrofielen \cdot aantal \, \, bacterien\] Dus \[k=\frac{1}{uur \cdot aantal \, \, neutrofielen}\]
Als je dit nog lastig vindt kan je 11.8 Rekenen aan eenheden nog een keer doorlezen!
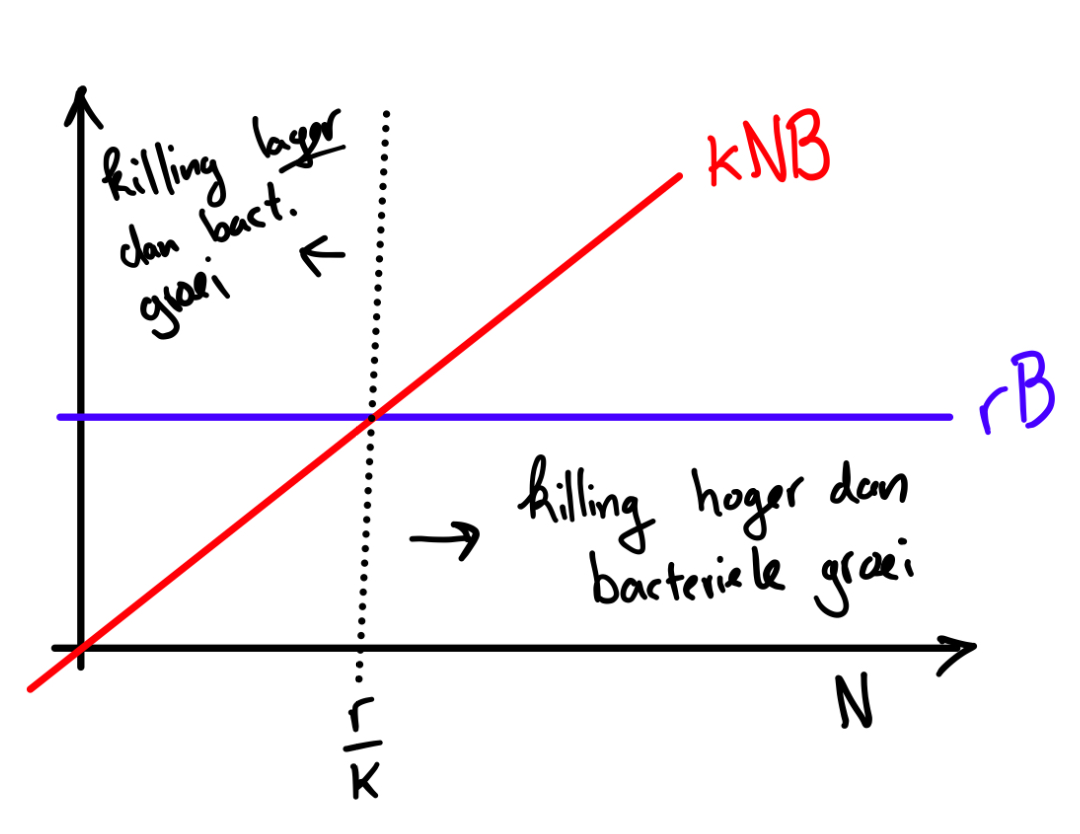
c. \[\begin{align*} \mathchoice{\frac{\mathrm{d}B} {\mathrm{d}t}}{\mathrm{d}B/\mathrm{d}t} {\mathrm{d}B/\mathrm{d}t} {\mathrm{d}B/\mathrm{d}t} &= 0 \\ rB-kNB &= 0 \\ B &= 0 \quad \text{(oplossing 1)} \\ r-kN &= 0 \\ kN &= r \\ N &= \frac{r}{k} \quad \text{(oplossing 2)} \\ \end{align*}\]
Er is dus een evenwicht in het aantal bacteriën als het aantal neutrofielen in het bloed precies gelijk is aan \(r/k\). Als het aantal neutrofielen lager is dan \(r/k\), zal het aantal bacteriën in het bloed toenemen. Als het aantal neutrofielen hoger is dan \(r/k\) zal het aantal bacteriën afnemen. De precieze hoeveelheid bacteriën in dit evenwicht kunnen we met dit model niet bepalen.
d.
Een goede schets ziet er ongeveer zo uit:
e. Om de groei van de bacteriën te stoppen moet \( \mathchoice{\frac{\mathrm{d}B} {\mathrm{d}t}}{\mathrm{d}B/\mathrm{d}t} {\mathrm{d}B/\mathrm{d}t} {\mathrm{d}B/\mathrm{d}t} \) gelijk zijn aan nul. We hebben deze vergelijking al opgelost in vraag c. \( \mathchoice{\frac{\mathrm{d}B} {\mathrm{d}t}}{\mathrm{d}B/\mathrm{d}t} {\mathrm{d}B/\mathrm{d}t} {\mathrm{d}B/\mathrm{d}t} =0\) als \(N=r/k\).
Je hebt dus \(r/k\) neutrofielen nodig om de groei van de bacteriën te stoppen. Dit punt is ook het snijpunt tussen de lijnen van Figuur 5. Dit is logisch, omdat de positieve en negatieve term van de vergelijking dan even groot zijn.
f. We moeten het aantal dode bacteriën delen door het aantal neutrofielen. Dus \(kNB/N = kB\). Per neutrofiel worden er dus \(kB\) bacteriën per uur opgeruimd.
g. Als er 0 bacteriën zijn, worden er 0 bacteriën per neutrofiel opgeruimd (want iets vermenigvuldigen met 0 geeft altijd 0). Dit is een redelijke aanname.
Als er oneindig veel bacteriën zijn, worden er oneindig veel bacteriën per neutrofiel doodgemaakt.
Op het moment dat er enorm veel bacteriën zijn, werken de neutrofielen dus ook enorm snel. Dit is geen redelijke aanname, want elke neutrofiel kan per uur maar een gelimiteerd aantal bacteriën opruimen. Het zou dus logischer zijn als er een limiet zit op deze term: het aantal bacteriën dat een neutrofiel maximaal kan opruimen per uur.
h. Als \(B\) heel groot is, dan maakt de kleine toevoeging van \(h\) onderin de breuk niet heel veel meer uit. \(h\) wordt dus voor grote waarden van \(B\) “verwaarloosbaar”.
i. Laten we even kijken wat er gebeurt met de term \(\frac{kNB}{h+B}\) als \(B\) heel groot is:
\[\frac{kNB}{h+B}\] \[\frac{kN}{h/B+B/B}\] \[\frac{kN}{h/B+1}\]
Doordat \(B\) heel groot is geldt \(h/B \rightarrow 0\). De term als geheel benadert dan \(kN\).
In andere woorden: als \(B\) heel groot is ten opzichte van \(h\), dan kan je de breuk vereenvoudigen tot \(\frac{kNB}{B}\) en de \(B\)’s wegstrepen en houd je alleen \(kN\) over. Per neutrofiel worden er dus hoogstens \(k\) bacteriën doodgemaakt, zelfs als er oneindig veel bacteriën zijn. Doordat er een grens zit aan het aantal bacteriën dat een neutrofiel per uur kan verwijderen is dit model realistischer dan in de eerste versie.
j. Om de groei te stoppen moet gelden: \( \mathchoice{\frac{\mathrm{d}B} {\mathrm{d}t}}{\mathrm{d}B/\mathrm{d}t} {\mathrm{d}B/\mathrm{d}t} {\mathrm{d}B/\mathrm{d}t} = 0\). \[\begin{align*} \mathchoice{\frac{\mathrm{d}B} {\mathrm{d}t}}{\mathrm{d}B/\mathrm{d}t} {\mathrm{d}B/\mathrm{d}t} {\mathrm{d}B/\mathrm{d}t} &= 0 \\ rB-\frac{kNB}{h+B} &= 0 \\ B\left(r-\frac{kN}{h+B}\right) &= 0 \\ B &= 0 \quad \text{(oplossing 1)} \\ r-\frac{kN}{h+B} &= 0 \\ \frac{kN}{h+B} &= r \\ kN &= r(h+B) \\ N &= \frac{r(h+B)}{k} \quad \text{(oplossing 2)} \end{align*}\]
We hebben dus minimaal \(\frac{r(h+B)}{k}\) neutrofielen nodig. Het valt je misschien op dat het aantal neutrofielen dat we nu nodig hebben om de groei van de bacteriën te stoppen nu wel afhankelijk is van het aantal bacteriën \(B\). Doordat elke neutrofiel nu een beperkt aantal bacteriën per uur kan opruimen, hebben we dus meer neutrofielen nodig als er meer bacteriën zijn!
a. Als de geboorte- en sterftensnelheid aan elkaar gelijk zijn blijft de populatie in evenwicht, omdat er dan ongeveer net zoveel Heckrunderen geboren worden als er dood gaan. Uit de grafiek kun je aflezen dat dit het geval is bij een populatie van ongeveer 340 tot 350 runderen.
b.
Om deze vragen te beantwoorden moet je allereerst inzien dat lijnen in de figuur overeenkomen met de termen \({\color{#2a53f7}b}\left(1-\frac{N}{K_b}\right)N\) (de dalende geboortelijn), en \({\color{red}d}\left(1+\frac{N}{K_d}\right)N\) (de stijgende sterftelijn).
Daarnaast kunnen we bepaalde dingen aflezen, bijvoorbeeld dat de maximale geboorte 40% (dus \(b=0.4\)) is. Ook weten we dat de runderen met een populatiegroote van 400 maar de helft van de deze maximale geboorte hebben. Zodoende kunnen we ook de laatste onbekende (\(K_b\)) bepalen:
\[\frac{1}{2} \cdot 0.4 = 0.4 \cdot \left(1-\frac{400}{K_b}\right)\] \[\frac12= 1-\frac{400}{K_b}\] \[-\frac{1}{2} = -\frac{400}{K_b}\] \[\frac{2}{1}=\frac{K_b}{400}\] \[K_b = 400\cdot 2 = 800\]
c. Op dezelfde manier als bij b lezen we af aan de grafiek dat de minimale sterfte 3% is. Dus \(d=0.03\).
Daarna kunnen we \(K_d\) uitrekenen: \[0.33 = 0.03\left(1+\frac{500}{K_d}\right)\] \[\frac{0.33}{0.03} = 11 = 1+\frac{500}{K_d}\] \[ 10 = \frac{500}{K_d}\] \[\frac{10}{500} = \frac 1{K_d}\] \[K_d = \frac{500}{10} = 50 \]
d. Als we al onze gevonden parameters invullen krijgen we de volgende ODE: \[\frac{dN}{dt} = 0.4\left(1-\frac{N}{800} \right) N - 0.03 \left(1+\frac{N}{50}\right)N\] Deze stellen we gelijk aan 0 om het evenwicht te bepalen: \[0= 0.4\left(1-\frac{N}{800} \right) N - 0.03 \left(1+\frac{N}{50}\right)N\] \[N=0 \quad \text{ (triviale oplossing), of...} \] \[0.4\left(1-\frac{N}{800} \right) = 0.03 \left(1+\frac{N}{50}\right)\] We negeren de triviale oplossing, en bepalen N uit de andere vergelijking: \[0.4-\frac{0.4N}{800} = 0.03+\frac{0.03N}{50}\] \[0.4-0.03 = \left(\frac{0.4}{800}+\frac{0.03}{50} \right)N\] \[0.37 = 0.0011N\] \[N\approx 336\]
Dit is inderdaad de hoeveelheid die we uit de grafiek hebben afgelezen, dus we hebben waarschijnlijk de parameters juist bepaald!
e. Het aantal dieren die elk jaar dood gaan is gelijk aan \(d\left(1-\frac N{K_d}\right)N\) waarin we onze waardes in kunnen vullen: \[0.03 \cdot \left(1+\frac{336}{50}\right) \cdot 336\approx 78\] Er gaan dus 78 runderen per jaar dood.
f. Na 300 tijdstappen wordt er begonnen met afschieten (if(t>300) k <- 0.05). Maar let op! Dit komt overeen met 30 jaar omdat de tijdstap 0.1 jaar is (delta_t <- 0.1 # grootte van de tijdstap).
Er wordt telkens 5% van de populatie afgeschoten omdat \(k\) gelijk gesteld wordt aan 0.05.
g. De sterfte (inclusief afschieten!) neemt met minder dan 5% toe (ongeveer 2.3 procent), terwijl er wel 5% extra wordt afgeschoten. De lagere dichtheid lijkt dus deels te compenseren voor het afschieten, er gaat ~2.7% van de populatie minder dood dan je naïef zou verwachten. Deze dieren waren anders wellicht van de honger overleden.
h. De dieren leven iets minder lang, maar gaan wel relatief minder vaak dood van de honger. Daarom zou het aangemoedigd kunnen worden.
i. Vooral oude dieren afschieten. Hierdoor veranderd de deathrate eigenlijk nauwelijks, en gaan er ook minder jonge dieren dood omdat de oude dieren minder “voedsel verspillen”. Overigens is het ethische debat hier niet meteen mee opgelost, want oudere dieren hebben ook recht op leven. In ieder geval kunnen we met dit model de effecten van het afschieten beter kwantificeren, in plaats van deze discussie alleen op gevoelens te laten bazeren.
Antwoorden 13 Ruimtelijke groei
a. Ja, met een lagere begin-dichtheid krijg je wel een mooie logistische groeicurve.
b. Soms sterft iedereen uit omdat ze van elkaar gescheiden zijn en elkaar niet kunnen helpen.
c. Je antwoord kan veel verschillen van dit antwoordenmodel, want het is een stochastisch process. Meestal lukt het de populaties ongeveer 5/20 keer om uit te groeien, maar soms lukt het ze helemaal nooit!
d. Het lukt de populatie nu veel vaker (bijna altijd) om succesvol uit te groeien.
e. Je zou duidelijk een verschil moeten zien. Maar het zou natuurlijk toeval kunnen zijn. In het onderdeel ‘Statistiek’ ga je leren hoe je toch uitspraken kan doen over deze onzekere data.
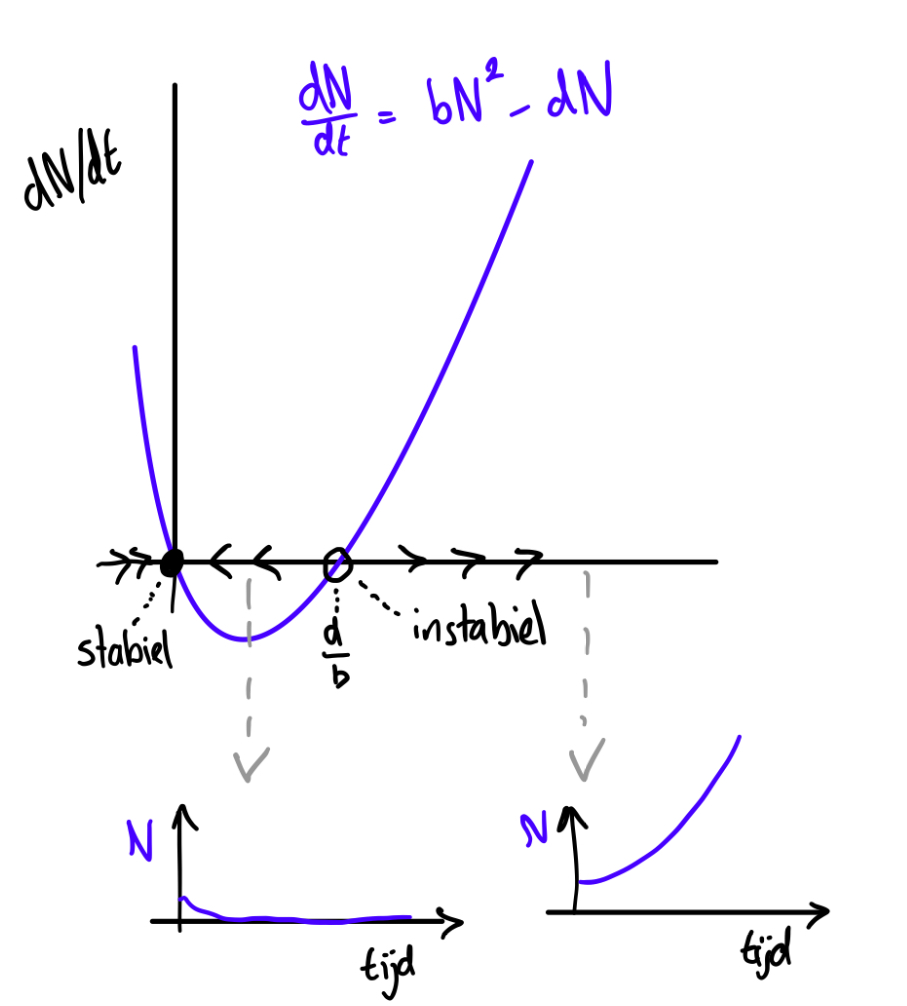
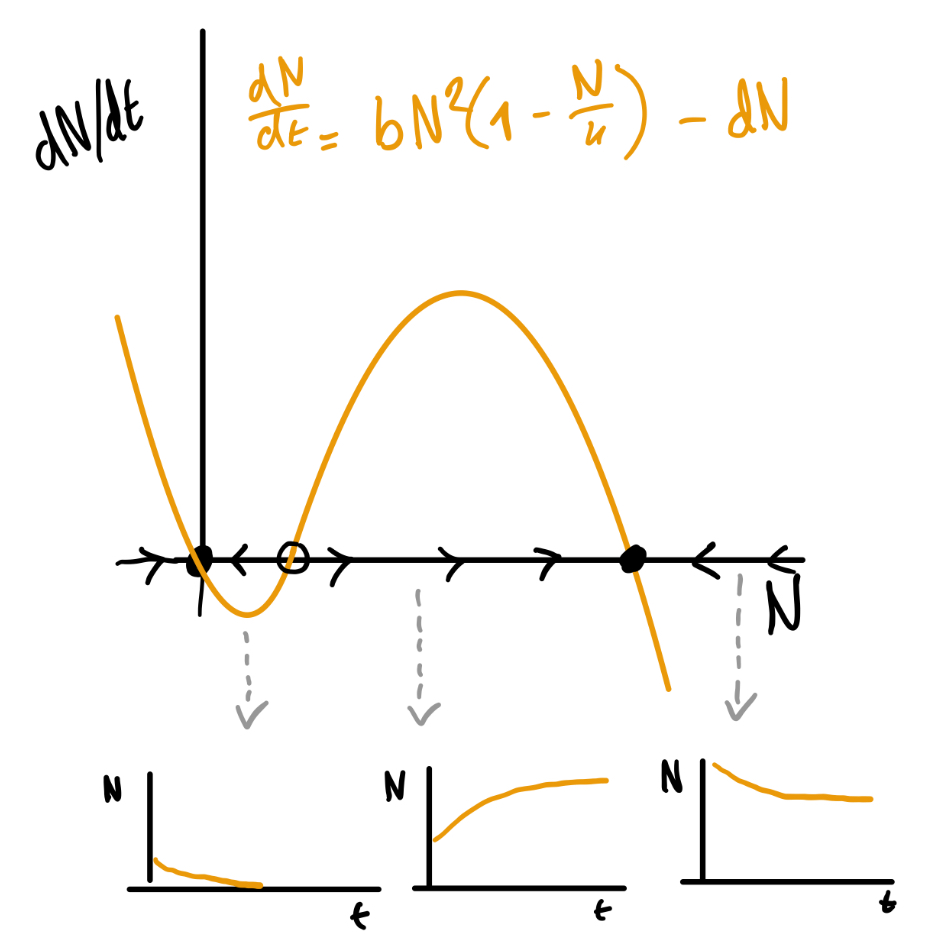
a. \[\frac{dN}{dt}=0=bN^2-dN\] \[N(bN-d)=0\] \[N=0 \quad \text{ of } \quad bN-d=0 \rightarrow N=\frac{d}{b}\]
b/c
Een faseportret met oplossingen zal er voor dit model ongeveer zo uit zien:
\(N=0\) is stabiel, \(\frac db\) is instabiel. Bij een kleine populatiegrootte zal er dus geen groei zijn, maar als de populatiegroote hoog genoeg is zal de populatie oneindig door kunnen groeien.
d. In het individual-based model gingen we er van uit dat er maar 1 individu in een hokje past. Hierdoor kan de populatie niet exponentieel toe blijven nemen, want na een tijdje zitten alle hokjes vol en kunnen er pas weer nieuwe indviduen komen als er eerst weer een paar dood zijn gegaan.
a.
Je schets zou identiek moeten zijn aan de rechterzijde van Figuur 12.2:
b+c.
Het faseportret met oplossingen zal er ongeveer zo uit zien:
Er zijn drie mogelijke opties voor de oplossingen:
- De populatie begint te klein en neemt af tot 0.
- Er zijn genoeg individuen om te groeien, dus groeit de populatie tot een evenwicht.
- We beginnen met een hele grote populatie, die exponentieel afneemt tot aan de stabliele evenwichtsstand.
a. In dit systeem hebben alle drie de soorten er wat aan als er meer gemengd wordt. Ze hebben namelijk allemaal iemand anders nodig om zich voort te planten, en als er niet gemengd wordt zullen ze vooral bij hun eigen soort in de buurt zitten. Bovendien is hier ook geen mogelijkheid voor 1 soort om de anderen uit te roeien, omdat er altijd een andere is die deze groei weer tegen kan gaan.
b. Er onstaan een soort golven die omzichzelf heen krullen, en zo spiralen vormen. Je ziet de populatiegroottes elkaar steeds opvolgen.
c. Mengen+ zorgt voor te grote fluctuaties, waardoor 1 soort volledig uit kan sterven. Hierdoor valt de hele cyclus uit elkaar en gaat uiteindelijk iedereen dood. Mengen kan dus zowel goede als slechte effecten hebben op samenwerking, wat vooral afhangt van de specifieke tijdschalen.
Antwoorden 14 Predator-prooi interacties
a. De parameter \(\beta\) bepaalt hoe snel zeehonden via de term \(\beta ZI\) in de zieke zeehonden populatie terecht komen (ze verdwijnen uit de gezonde populatie, en komen erbij in de zieke populatie). De term \(\beta ZI\) is dus een infectieterm. De parameter \(\delta\) bepaalt hoe vaak zieke zeehonden dood gaan.
b. Ja, wel gegeven de modelomschrijving, want daar staat dat de zeehonden die ziek zijn snel dood gaan.
c. Het is dan een 1D systeem: \[ \mathchoice{\frac{\mathrm{d}Z} {\mathrm{d}t}}{\mathrm{d}Z/\mathrm{d}t} {\mathrm{d}Z/\mathrm{d}t} {\mathrm{d}Z/\mathrm{d}t} = bZ\left(1-\frac{Z}{k}\right)-dZ\] Deze vergelijking gelijkstellen aan 0 geeft \(Z = k\left(1-\frac{d}{b}\right)\). Dit is het evenwicht van de gezonde populatie in afwezigheid van de infectieziekte.
d. Ja, de populatie wordt kleiner. De populatiegrootte zonder infectieziekte wordt bepaald door \(k(1-d/b)\). Met kleinere \(b\) wordt d/b groter, dus de evenwichtwaarde kleiner. De populatie zal dus afnemen door de PCB’s. Tip: als je het moeilijk vindt om dit voor te stellen vul dan waarden in voor d en b.
e. Stel beide vergelijkingen gelijk aan 0.
Nullcline van Z: \[\begin{align*} bZ\left(1-\frac Zk\right) - dZ - \beta ZI &= 0 \\ Z\left(b\left(1-\frac Zk\right) - d - \beta I\right) &= 0 \\ Z &= 0 \quad \text{(oplossing 1)} \\ b\left(1-\frac Zk\right) - d - \beta I &= 0 \\ \beta I &= b\left(1-\frac Zk \right) - d \\ I &= \frac{b\left(1-\frac Zk \right) - d}{\beta} \quad \text{(oplossing 2)} \end{align*}\]
Nullcline van I: \[\begin{align*} \beta ZI - \delta I &= 0 \\ I(\beta Z - \delta) &= 0 \\ I &= 0 \quad \text{(oplossing 1)} \\ \beta Z - \delta &= 0 \\ \beta Z &= \delta \\ Z &= \frac \delta\beta \quad \text{(oplossing 2)} \end{align*}\]
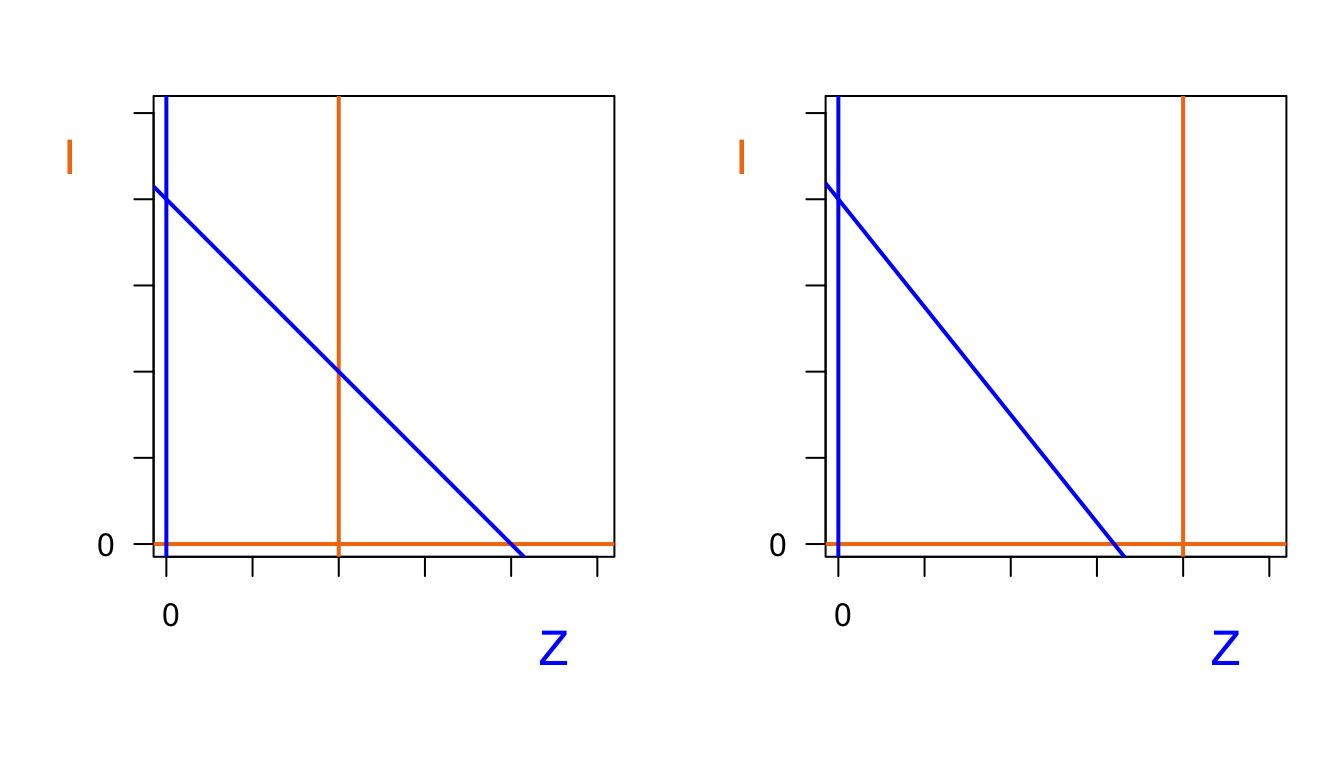
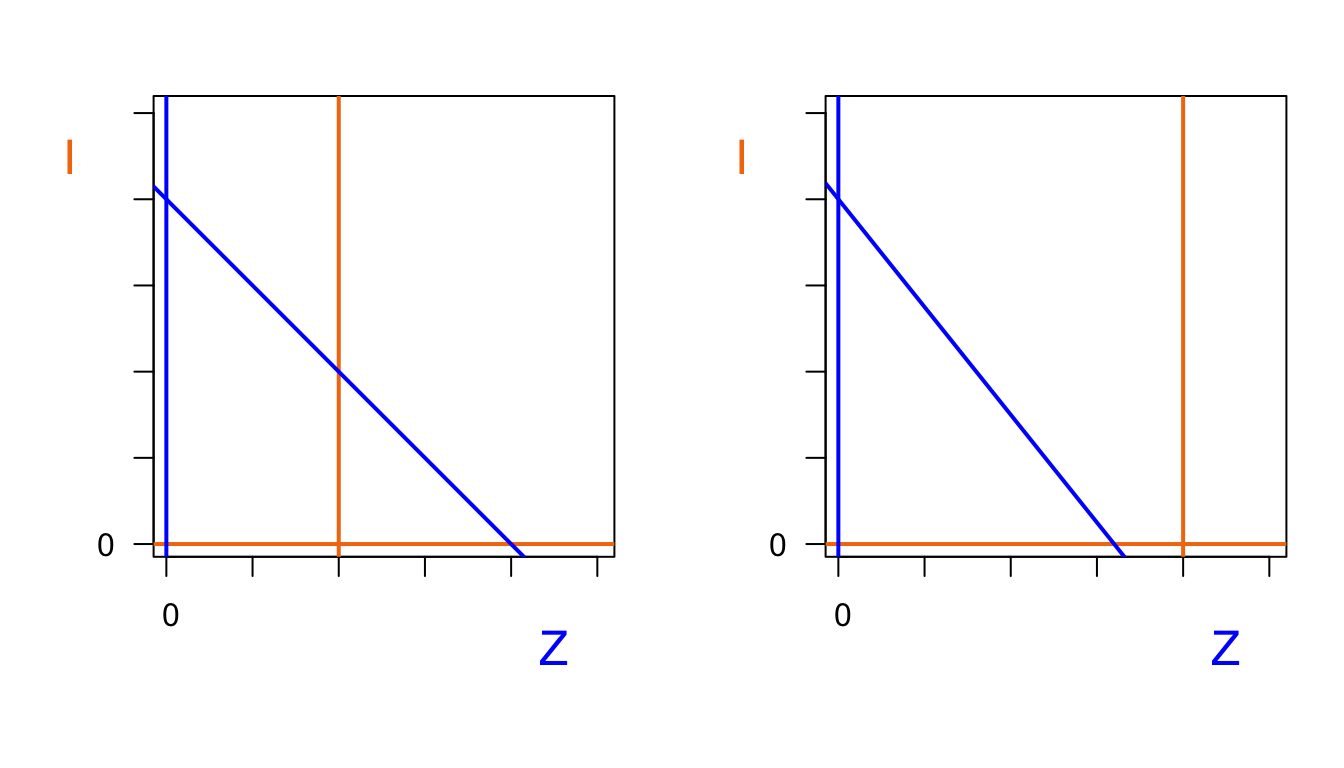
Er zijn twee kwalitatief verschillende situaties: één waarbij de twee nullclines elkaar snijden, en één waarbij er geen snijpunt is.
Hier is de R code om deze lijnen te schetsen, maar een simpele schets voldoet ook.
I <- 1:100
Z <- 1:100
par(pty="s",mfrow=c(1,2),mar=c(4,4,1,1.5))
plot(I,Z, col.axis="#f2790f",type='n',xaxt='n',xlab="",ylab="",axes=FALSE, frame.plot=TRUE)
mtext("Z", side=1, line=2, col="blue", cex=1.5, at=90)
mtext("I", side=2, line=2, col="#f2790f", cex=1.5,adj=1,las=2, at=90)
mtext("0", side=2, line=1, col="black", cex=1,adj=1,las=2, at=0)
mtext("0", side=1, line=1, col="black", cex=1,adj=0,las=1, at=-1)
Axis(side=1, labels=FALSE)
Axis(side=2, labels=FALSE)
abline(h=0, lwd=2, col="#f2790f")
abline(v=40, lwd=2, col="#f2790f")
abline(v=0, lwd=2, col="blue",)
abline(a=80,b=-1, lwd=2,col="blue")
plot(I,Z, col.axis="#f2790f",type='n',xaxt='n',xlab="",ylab="",axes=FALSE, frame.plot=TRUE)
mtext("Z", side=1, line=2, col="blue", cex=1.5, at=90)
mtext("I", side=2, line=2, col="#f2790f", cex=1.5,adj=1,las=2, at=90)
mtext("0", side=2, line=1, col="black", cex=1,adj=1,las=2, at=0)
mtext("0", side=1, line=1, col="black", cex=1,adj=0,las=1, at=-1)
Axis(side=1, labels=FALSE)
Axis(side=2, labels=FALSE)
abline(h=0, lwd=2, col="#f2790f")
abline(v=80, lwd=2, col="#f2790f")
abline(v=0, lwd=2, col="blue",)
abline(a=80,b=-1.25, lwd=2,col="blue")
f. Er is een evenwicht op een plek waar de oranje en blauwe lijn elkaar kruizen. Er zijn meerdere evenwichten. Evenwicht 1 is (0 ; 0): als er geen zeehonden zijn. De schuine nullcline (van \(Z\)) kan op twee punten de oranje lijnen snijden. We weten echter nog niet de precieze coördinaten van deze snijpunten, hier kunnen we achter komen door de waarde die we wel weten in te vullen in de formule van de \(Z\)-nullcline. Evenwicht 2: \(I = 0\) invullen in de \(Z\)-nullcline \(I = -Z\frac{b}{k\beta} + \frac{b - d}{\beta}\). \[\begin{align*} -Z\frac{b}{k\beta} + \frac{b - d}{\beta} &= 0 \\ Z\frac{b}{k\beta} &= \frac{b - d}{\beta} \\ Z &= \frac{b - d}{\beta} \cdot \frac{k\beta}{b} \\ Z &= \frac{k\beta(b - d)}{\beta b} \\ Z &= \frac{k(b - d)}{b} \\ Z &= \frac{kb - kd}{b} \\ Z &= k - \frac{kd}{b} \end{align*}\] Dus hier is een evenwicht voor \(I=0\) en \(Z = k - \frac{kd}{b}\). Evenwicht 3: \(Z = \delta / \beta\) invullen in de \(Z\)-nullcline \(I = -Z\frac{b}{k\beta} + \frac{b - d}{\beta}\). \[\begin{align*} I &= -Z\frac{b}{k\beta} + \frac{b - d}{\beta} \\ I &= -\frac{\delta}{\beta} \cdot \frac{b}{k\beta} + \frac{b - d}{\beta} \\ I &= -\frac{\delta b}{k \beta^2} + \frac{b - d}{\beta} \end{align*}\]
f.
Code
vectorfield <- function(x,y,dx,dy){
arrows(x, y, x+0, y+dy, length = 0.07, angle = 20, col="#f2790f",lwd=2)
arrows(x, y, x+dx, y+0, length = 0.07, angle = 20, col="blue",lwd=2)
}
I <- 1:100
Z <- 1:100
par(pty="s",mfrow=c(1,1),mar=c(4,4,1,1.5))
plot(I,Z, col.axis="#f2790f",type='n',xaxt='n',xlab="",ylab="",axes=FALSE, frame.plot=TRUE)
mtext("Z", side=1, line=2, col="blue", cex=1.5, at=90)
mtext("I", side=2, line=2, col="#f2790f", cex=1.5,adj=1,las=2, at=90)
mtext("0", side=2, line=1, col="black", cex=1,adj=1,las=2, at=0)
mtext("0", side=1, line=1, col="black", cex=1,adj=0,las=1, at=-1)
Axis(side=1, labels=FALSE)
Axis(side=2, labels=FALSE)
abline(h=0, lwd=2, col="#f2790f")
abline(v=40, lwd=2, col="#f2790f")
abline(v=0, lwd=2, col="blue",)
abline(a=80,b=-1, lwd=2,col="blue")
vectorfield(15,95,-10,-10)
vectorfield(95,12,-10,10)
vectorfield(50,12,10,10)
vectorfield(15,12,10,-10)
points(40,40,cex=1.3,pch=19)
text(55,40,"Evenwicht 3", cex=0.7)
points(0,0,cex=1.3)
text(12,5,"Evenwicht 1", cex=0.7)
points(80,0,cex=1.3)
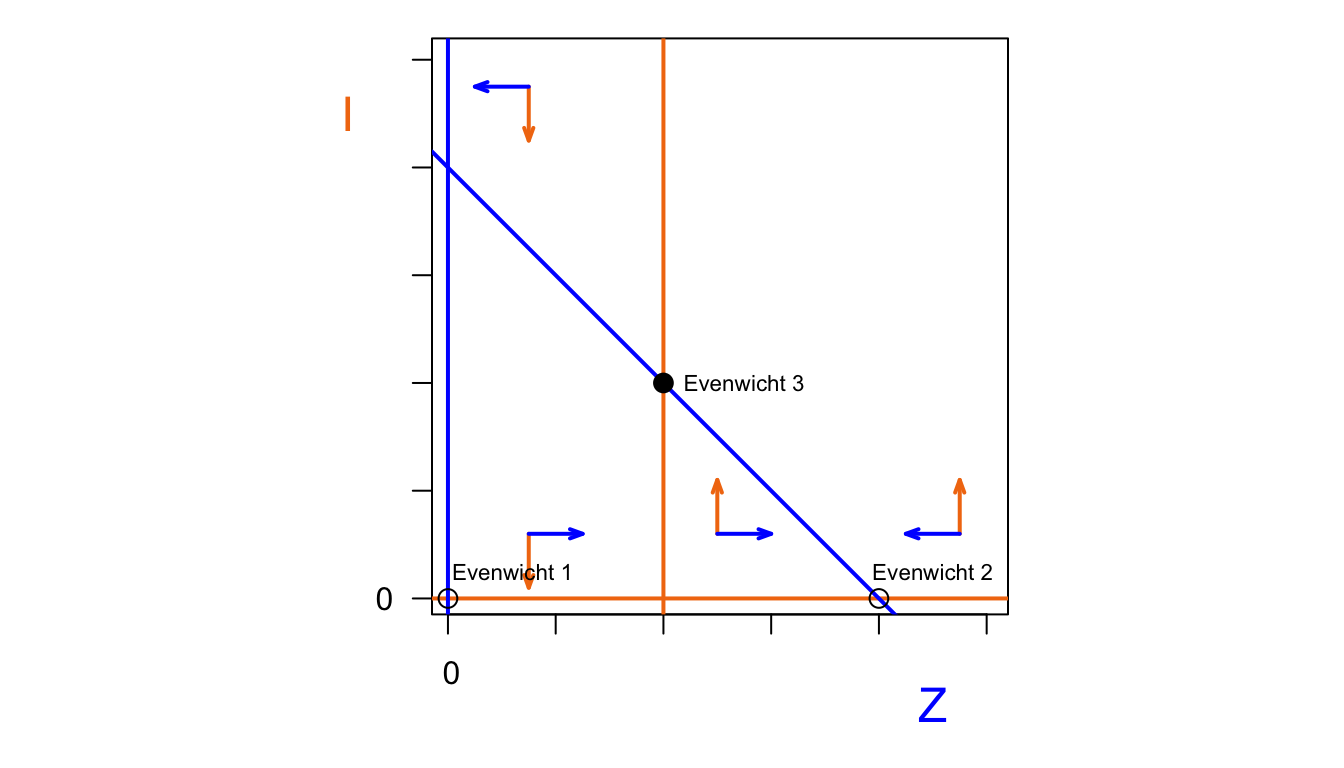
text(90,5,"Evenwicht 2", cex=0.7)
Code
par(pty="s",mfrow=c(1,1),mar=c(4,4,1,1.5))
plot(I,Z, col.axis="#f2790f",type='n',xaxt='n',xlab="",ylab="",axes=FALSE, frame.plot=TRUE)
mtext("Z", side=1, line=2, col="blue", cex=1.5, at=90)
mtext("I", side=2, line=2, col="#f2790f", cex=1.5,adj=1,las=2, at=90)
mtext("0", side=2, line=1, col="black", cex=1,adj=1,las=2, at=0)
mtext("0", side=1, line=1, col="black", cex=1,adj=0,las=1, at=-1)
Axis(side=1, labels=FALSE)
Axis(side=2, labels=FALSE)
abline(h=0, lwd=2, col="#f2790f")
abline(v=80, lwd=2, col="#f2790f")
abline(v=0, lwd=2, col="blue",)
abline(a=80,b=-1.25, lwd=2,col="blue")
vectorfield(50,60,-10,-10)
vectorfield(95,50,-10,10)
vectorfield(20,30,10,-10)
points(0,0,cex=1.3)
text(12,5,"Evenwicht 1", cex=0.7)
points(64,0,cex=1.3,pch=19)
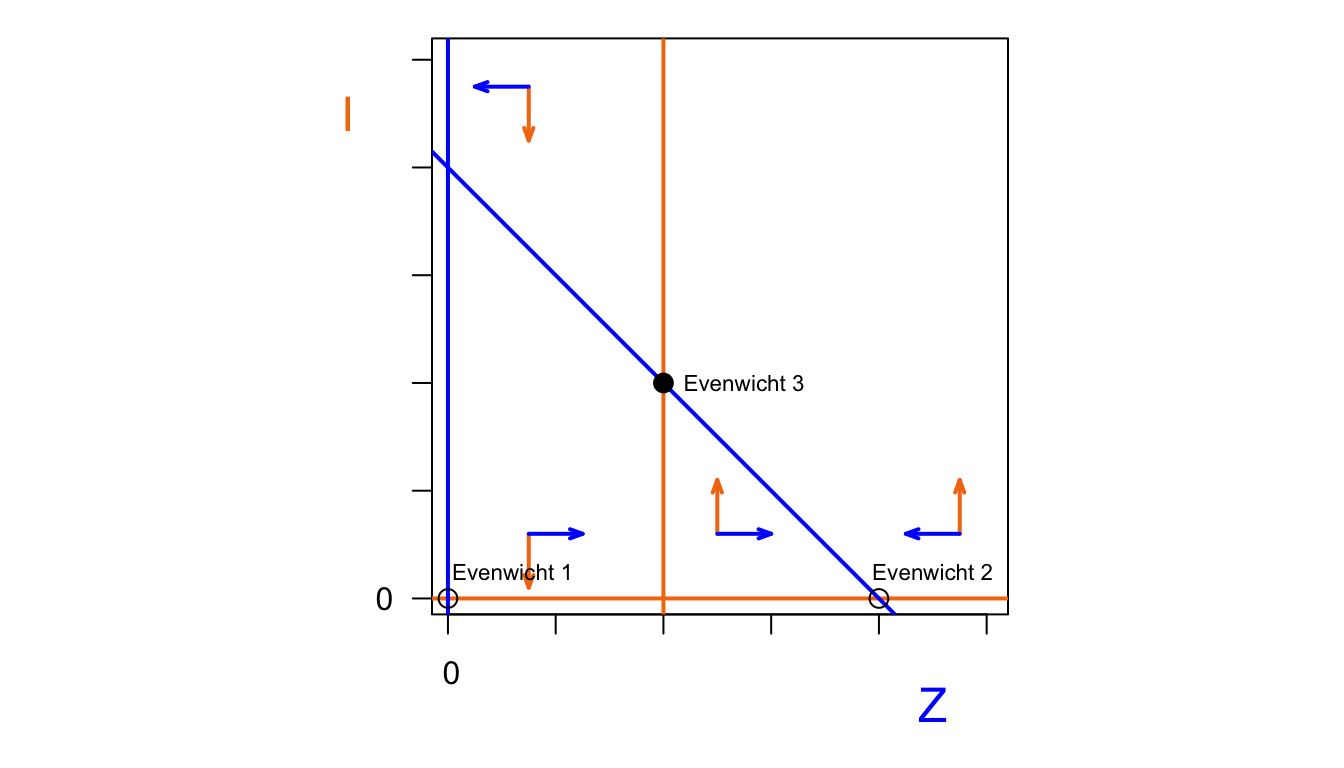
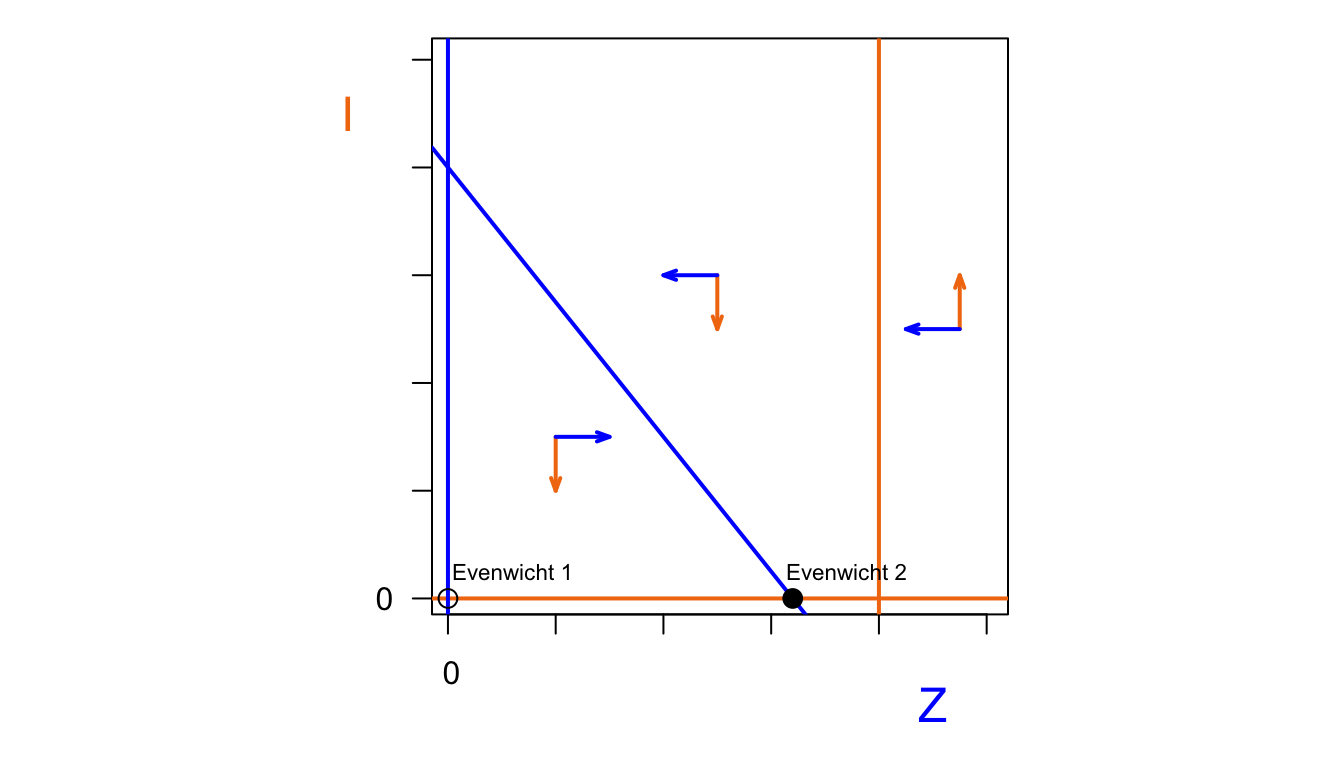
text(74,5,"Evenwicht 2", cex=0.7)
Het aantal geïnfecteerde zeehonden \(I\) stijgt als we aan de rechterkant van de \(I\)-nullcline zitten. Er zijn dan genoeg zeehonden om te infecteren. Links van de \(I\)-nullcline daalt het aantal geïnfecteerde zeehonden. Het aantal zeehonden stijgt als we ons onder de \(Z\)-nullcline bevinden. In de figuur hierboven zijn deze vectoren getekend in beide situaties. Nu kunnen we bekijken welke van de evenwichten stabiel zijn. Evenwicht 1 is niet stabiel, want zo gauw er kleine populatie zeehondenn is, zal deze populatie gaan groeien. De stabiliteit van evenwicht 2 hangt af van de specifieke situatie. In het geval dat de \(I\)-nullcline zich rechts van dit evenwicht bevindt (tweede plot hierboven), is het een stabiel evenwicht. De infectieziekte verdwijnt dan uit de populatie, en er is een evenwicht met alleen gezonde zeehonden. Als de \(I\)-nullcline zich links van dit evenwicht bevindt, is dit evenwicht niet meer stabiel. De infectieziekte blijft dan wel aanwezig in de populatie. Dit geeft dan een derde evenwichtssituatie, die ook stabiel is. In dit evenwicht zijn er zowel gezonde als zieke zeehonden.
g. De locatie van de \(I\)-nullcline wordt bepaald door \(\beta\) en \(\delta\). Als de ziekte niet infectieus genoeg is (\(\beta\) is te klein) of als de geïnfecteerde zeehonden te snel dood gaan (\(\delta\) is te groot) zal de ziekte te snel weer uit de populatie verdwijnen.
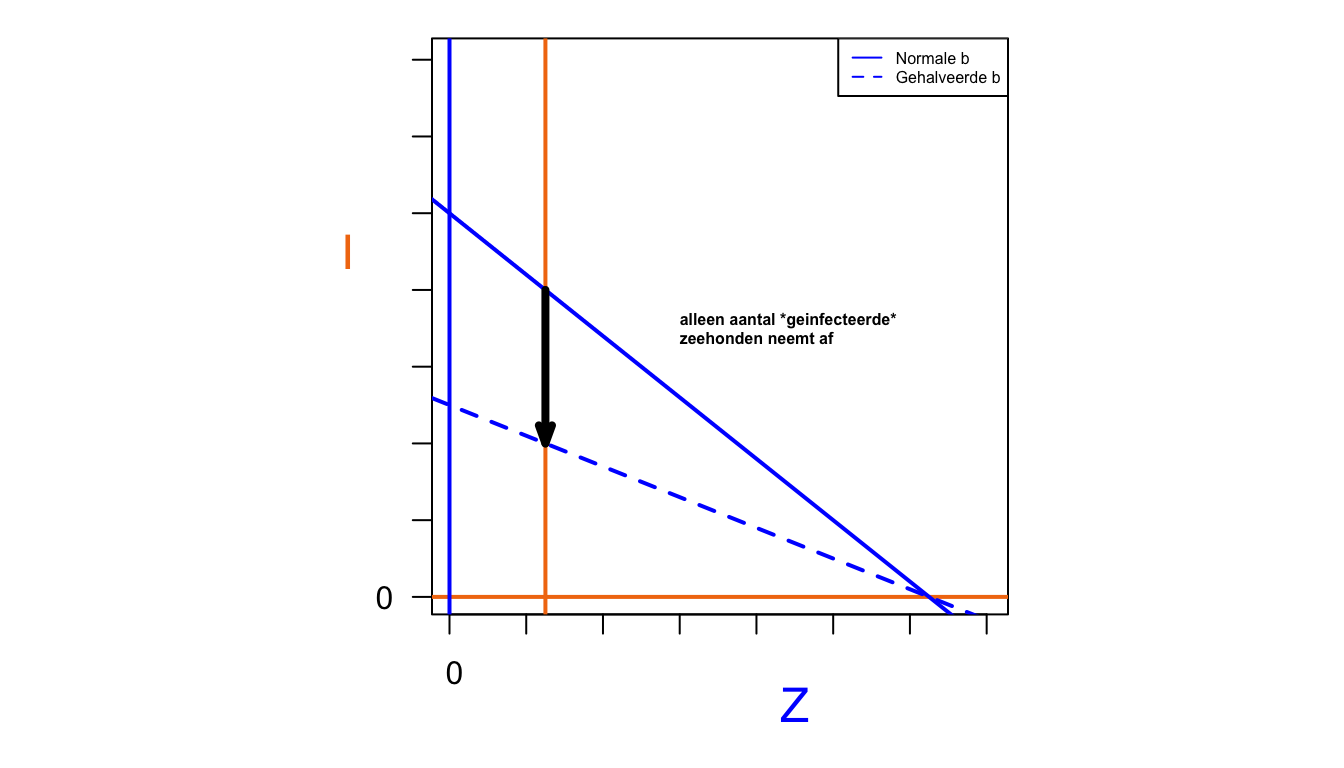
h. Alleen de nullcline van de gezonde zeehonden wordt beïnvloed door de geboortesnelheid van gezonde zeehonden, want daar staat \(b\) in:
\[I = \frac{b\left(1-\frac Zk \right) - d}{\beta}\]
Als b gehalveerd wordt krijgen we dus:
\[I = \frac{0.5b\left(1-\frac Zk \right) - d}{\beta}\]
Deze lijn begint dus bij een lagere waarde, maar zal ook langzamer dalen. Het snijpunt ligt daardoor precies bij dezelfde waarde van Z:
Code
vectorfield <- function(x,y,dx,dy){
arrows(x, y, x+0, y+dy, length = 0.07, angle = 20, col="#f2790f",lwd=2)
arrows(x, y, x+dx, y+0, length = 0.07, angle = 20, col="blue",lwd=2)
}
I <- 1:140
Z <- 1:140
par(pty="s",mfrow=c(1,1),mar=c(4,4,1,1.5))
plot(I,Z, col.axis="#f2790f",type='n',xaxt='n',xlab="",ylab="",axes=FALSE, frame.plot=TRUE)
mtext("Z", side=1, line=2, col="blue", cex=1.5, at=90)
mtext("I", side=2, line=2, col="#f2790f", cex=1.5,adj=1,las=2, at=90)
mtext("0", side=2, line=1, col="black", cex=1,adj=1,las=2, at=0)
mtext("0", side=1, line=1, col="black", cex=1,adj=0,las=1, at=-1)
Axis(side=1, labels=FALSE)
Axis(side=2, labels=FALSE)
abline(h=0, lwd=2, col="#f2790f")
abline(v=25, lwd=2, col="#f2790f")
abline(v=0, lwd=2, col="blue",)
abline(a=100,b=-0.8, lwd=2,col="blue")
abline(a=50,b=-0.4, lwd=2,col="blue", lty=2)
# add a black arrow pointing down in the middle of the plot
arrows(25, 80, 25, 40, length = 0.1, angle = 20, col="black",lwd=4)
# add text saying "alleen aantal geinfecteerde zeehonden neemt af", met een stippellijn verbonden met het midden van de pijl, verdeeld over twee regels en met een witten achtergrondkleur zodat het leesbaar is
text(60, 70, "alleen aantal *geinfecteerde* \nzeehonden neemt af", adj=0, cex=0.5, col="black", font=2, bg="white")
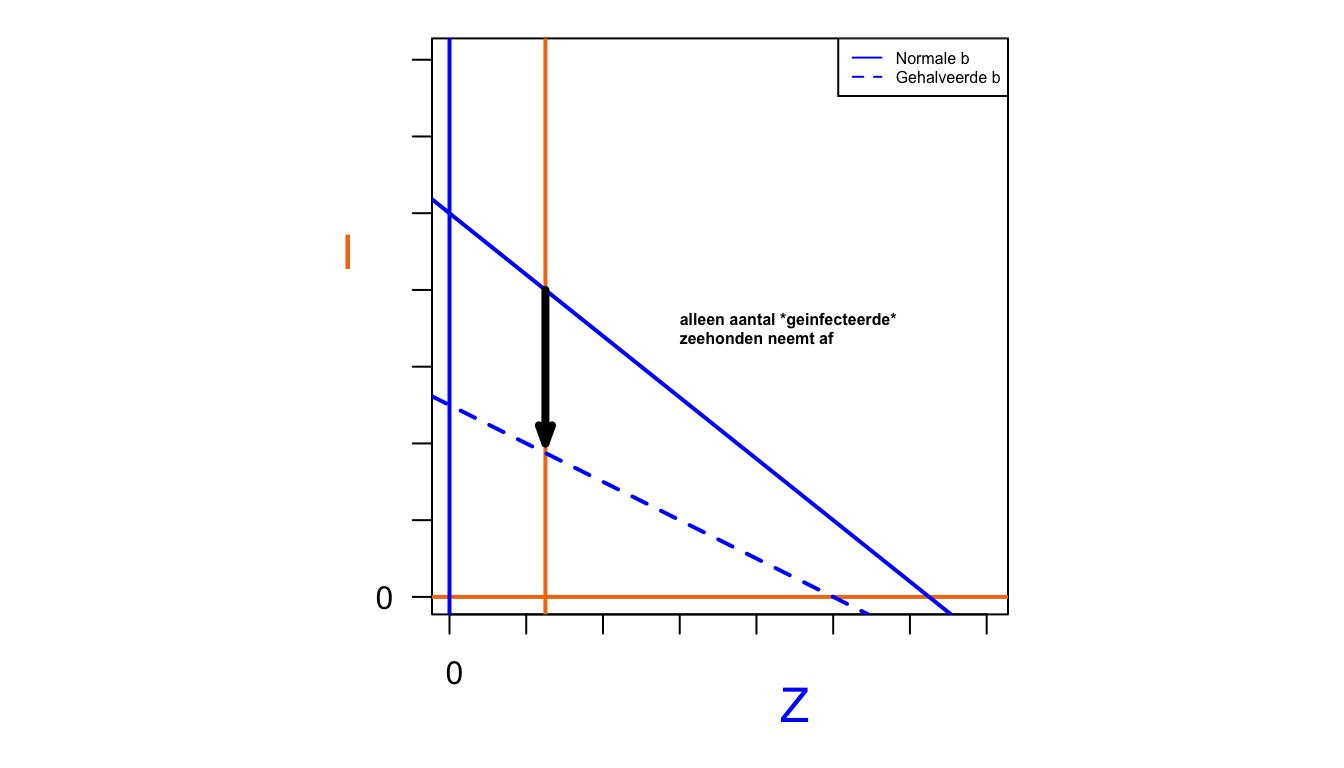
legend("topright", legend=c("Normale b", "Gehalveerde b"), col=c("blue", "blue"), lty=1:2, cex=0.5)
i.
Het aantal gezonde zeehonden in evenwicht is helemaal niet kleiner geworden! De evenwichtswaarde van de hoeveelheid gezonde zeehonden is onafhankelijk van hun geboorte geworden, en wordt alleen bepaald door de ligging van de predatornullcline. Er zijn kennelijk vooral minder zieke zeehonden.
Mocht je het niet door hebben gehad: dit model is identiek aan het predator-prooi model dat we in dit hoofdstuk hebben besproken. Ook de conclusies komen overeen. Het feit dat de zieke zeehonden niet beïnvloed worden door hun geboorte, is hetzelfde fenomeen als de konijnen die een hogere birth rate hadden (bijvoorbeeld door meer te eten te hebben), maar toch niet in populatiegroote toenamen. Maar dit gaat alleen op als er ook daadwerkelijk een infectieziekte (of predator zoals bij de konijnen) aanwezig is. De mogelijke populatiegrootte (draagkracht) zonder ziekte is wel lager als we \(b\) halveren.
a. De parameter \(c\) (zoals uitgelegd voor het Lotka-Volterra predator/prooi model) is gelijk aan 1. Dit betekent dat we aannemen dat de biomassaconversie perfect is. Als er één prooihokje wordt opgegeten leidt dit tot de geboorte van één predatorhokje.
b. Ja, de resultaten van de simulatie lijken heel erg op Figuur 14.3. Eerst schommelen de populaties een beetje, maar de schommelingen worden steeds kleiner. Er zijn nog wel wat zeer kleine schommelingen. Dit is vooral doordat het model met kansen werkt.
c. Het systeem stabiliseert bij ~2300 prooi en ~11000 predator (bij de default 0.04 death rate predators). Er zijn dus meer predatoren dan prooi. Het voorbeeld van konijnen en vossen is hierbij niet geschikt, want er zullen (bij een systeem in evenwicht) altijd meer konijnen dan vossen zijn. Een situatie waarbij dit wel zou kunnen is bijvoorbeeld bij parasieten of virussen en hun gastheren. Een ander voorbeeld is wolven of leeuwen die in groepen op groot wild jagen.
d. Het systeem stabiliseert nu rond ~15000 predatoren en ~2000 prooi. Er zijn dus nóg meer predatoren, en iets minder prooi.
e. Bij mengen nemen de predatoren een stuk meer toe dan de prooi. Een predator kan makkelijker prooi vangen, omdat bij mengen de prooi waarschijnlijk veelal omringd is door predatoren. Daarnaast kan prooi ook makkelijker geboren worden (grotere kans op een leeg vakje naast je, omdat er geen structuur ontstaat). Maar in de opdrachten hiervoor hebben we al gezien dat het verhogen van de geboortesnelheid van prooi juist zorgt voor een toename van de hoeveelheid predatoren, en niet van de prooi.
f.
Het aantal predatoren neemt niet per se toe, maar er zijn wel sterkere schommelingen in het aantal predatoren. Het aantal prooien lijkt wel af te nemen. Je ziet nu ook duidelijk dat er een soort golven van prooi ontstaan die worden opgegeten door predatoren.
g. Met een hele lage death rate hebben de predatoren een hele kleine kans om dood te gaan. Je ziet eerst dat er daardoor bijna geen ruimte meer over is voor de prooi om zich te voort te planten. Hierdoor sterft de prooi na een tijdje uit. Als alle prooi dood is, sterven ook de predatoren langzaam uit (omdat ze geen eten meer hebben). Dit zou niet voor komen in een ODE, omdat daar niet met losse individuen gewerkt wordt. Er zou altijd nog 0.00001 prooi in leven kunnen zijn die daarna weer voort kan planten.
a. Alleen susceptible individuen planten zich individueel voort. De andere populatie planten kunnen wel groeien, maar alleen dankzij de aanwezigheid van een ander.
b. De eenheid van \( \mathchoice{\frac{\mathrm{d}I} {\mathrm{d}t}}{\mathrm{d}I/\mathrm{d}t} {\mathrm{d}I/\mathrm{d}t} {\mathrm{d}I/\mathrm{d}t} \) is \(I\) per tijdseenheid. Dus: \(\delta I = \frac It\) en \(\delta = \frac {1}{It} \cdot I = \frac 1t\). Dit kunnen we interpreteren als ‘per tijdseenheid’. Dus het geeft een verhoogde kans aan om dood te gaan als je bent geïnfecteerd met het virus.
c. De eerste piek van geïnfecteerden is het hoogst, omdat de er aan het begin erg veel varbare individuen (susceptibles) zijn. Daardoor is het relatief voor het virus om vatbare individuen te vinden die geïnfecteerd kunnen worden, en is er een enorme piek in het aantal infecties.
d. Onder gemengde omstandigheden gedraagd het ruimtelijke model zich bij benadering vergelijkbaar met het ODE model, maar niet precies. Het aantal geïnfecteerde indivuden lijkt bijvoorbeeld wat lager uit te komen. Dit heeft wellicht te maken met het feit dat een geïnfecteerd individu, ondanks het mengen, in 1 tijdstap alleen nabij gelegen individuen kan aansteken. Zo zie je dat een gemengde simulatie niet altijd precies hetzelfde doet als een ODE, omdat er stiekem nog andere subtiele verschillen kunnen izjn.
e. Het is meer vergelijkbaar met contactbeperkingen, want de pixels houden dezelfde afstand tot elkaar (er is dus geen “social distancing”). Echter heeft elke pixel alleen contact met de aangrenzende pixels, dus 1 individu kan per tijdstap hoogstends de 8 buren infecteren, en niet meer dan dat.
f. In het ongemengde systeem zie je dat het virus uitsterft, omdat het zich te snel verspreidt en daardoor alle vatbare individuen uitroeit. Kleine populaties vatbare individuen blijven echter achter en groeien uiteindelijk weer terug; maar het virus is al weg! In het gemengde systeem daarentegen sterft de gehele populatie uit: het agressieve virus kan altijd een nieuw slachtoffer vinden, waardoor er geen overlevenden zijn.
a. Dit betekent dat de biomassaconversie perfect is: elke A die opgegeten wordt levert 1 B op.
Dit geldt overigens ook voor conversie van B naar C.
Dit is een modelaanname, een mogelijk alternatief zou zijn om een extra term toe te voegen. Het eten van 1 A zou dan bijvoorbeeld kunnen zorgen voor een toename van 0.5 B. Met zo’n term nemen we dus aan dat conversie niet perfect is.
b. Alle drie de populaties zijn in evenwicht, dus \( \mathchoice{\frac{\mathrm{d}A} {\mathrm{d}t}}{\mathrm{d}A/\mathrm{d}t} {\mathrm{d}A/\mathrm{d}t} {\mathrm{d}A/\mathrm{d}t} = \mathchoice{\frac{\mathrm{d}B} {\mathrm{d}t}}{\mathrm{d}B/\mathrm{d}t} {\mathrm{d}B/\mathrm{d}t} {\mathrm{d}B/\mathrm{d}t} = \mathchoice{\frac{\mathrm{d}C} {\mathrm{d}t}}{\mathrm{d}C/\mathrm{d}t} {\mathrm{d}C/\mathrm{d}t} {\mathrm{d}C/\mathrm{d}t} = 0\). Als we kijken naar de vergelijkingen zien we dat het gelijkstellen van \( \mathchoice{\frac{\mathrm{d}C} {\mathrm{d}t}}{\mathrm{d}C/\mathrm{d}t} {\mathrm{d}C/\mathrm{d}t} {\mathrm{d}C/\mathrm{d}t} \) aan nul meteen een oplossing geeft voor \(B\). Namelijk: \[\begin{align*} eBC - fC &= 0 \quad \text{We weten dat $C \neq 0$, dus mogen delen door $C$} \\ eB - f &= 0 \\ eB &= f \\ B &= \frac fe \end{align*}\] We zien dus dat we of een triviale oplossing hebben waarbij we niet meer 3 populaties hebben (C=0), die in dit geval niet van toepassing is, of een oplossing voor een populatie van \(B\) waarbij er een evenwicht is. De populatiegroote van \(B\) is dus \(\frac fe\) als de populaties in evenwicht zijn.
Antwoorden ODEs modelleren in R
a. We hebben nu deze functie die de verandering in de prooi populatie beschrijft:
\[ \mathchoice{\frac{\mathrm{d}\textcolor{#2d43fc}{R}} {\mathrm{d}t}}{\mathrm{d}\textcolor{#2d43fc}{R}/\mathrm{d}t} {\mathrm{d}\textcolor{#2d43fc}{R}/\mathrm{d}t} {\mathrm{d}\textcolor{#2d43fc}{R}/\mathrm{d}t} = b\left(1-\frac{\textcolor{#2d43fc}{R}}{K}\right)\textcolor{#2d43fc}{R} - d\textcolor{#2d43fc}{R} - \frac{a\textcolor{#2d43fc}{R}\textcolor{orange}{N}}{h+\textcolor{#2d43fc}{R}}\]
Deze gaan we gelijk stellen aan 0 om de nullclines te bepalen:
\[0=b\left(1-\frac RK \right) R - dR - \frac{aRN}{h+R}\]
\[R=0 \quad \text{oplossing 1}\]
\[b\left(1-\frac RK \right) - d - \frac{aN}{h+R}=0\] Alles vermedigvuldigen met \(h+R\): \[b(h+R)\left(1-\frac RK \right) - d(h+R) - aN=0\]
We schrijven het op als \(N=f(R)\), omdat we \(N\) meestal op de y-as zetten en het hierdoor makkelijker te visualiseren is.
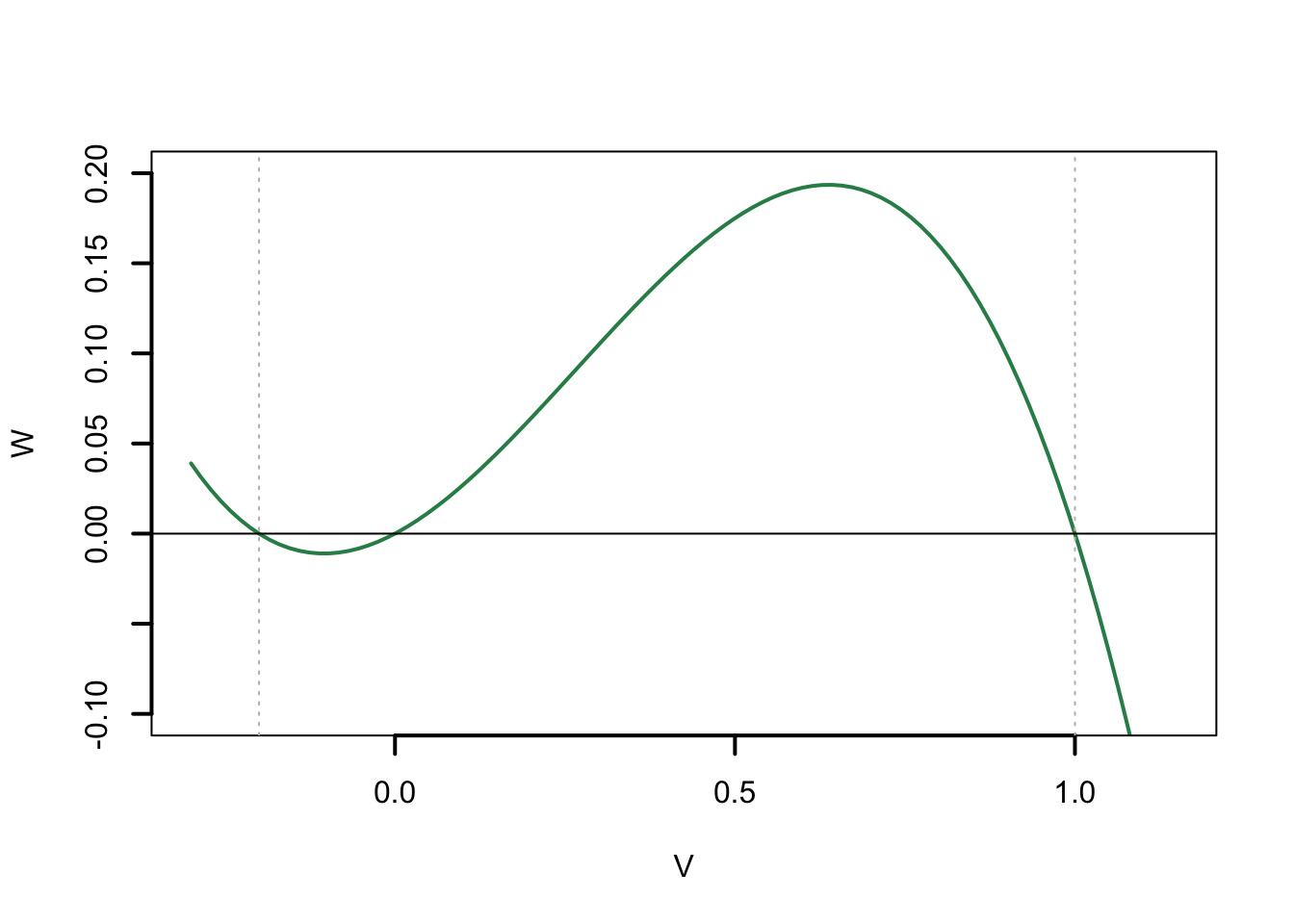
\[(h+R)\left(b\left(1-\frac{R}{K}\right)-d\right)=aN\] We kunnen nu al zien dat het een bergparabool zal vormen, omdat we een negatieve \(R^2\) term hebben. We delen nu nog door a en dan krijgen we:
\[\frac 1a(h+R)\left(b\left(1-\frac{R}{K}\right)-d\right)=N\]
b. K beinvloed de breedte van de parabool. De breedte van de parabool hangt af met de snijpunten met de R-as waar \(N=0\). Dit snijpunt komt overeen met de stabiele populatie prooidieren zonder roofdieren. Het eerste snijpunt heeft een negatieve R (\(h+R=0\Rightarrow R=-h\)) dus daar kunnen we geen nuttige biologische informatie uit halen. Het andere snijpunt is: \[b\left(1-\frac RK \right) -d = 0\] \[1-\frac RK = \frac db\] \[1-\frac db = \frac RK\] \[K \left(1-\frac db\right)=R\] Zoals je kan zien heeft \(K\) een directe invloed op het snijpunt en dus op de stabiele populatie prooidieren, wat ook logisch is want K wordt meestal gebruikt als de carrying capacity.
c.
source("https://tbb.bio.uu.nl/rdb/grindR/grind.R")grind.R (25-06-2024) was sourcedmodel <- function(t, state, parms) {
with(as.list(c(state,parms)), {
dR <- r*R*(1 - R/K) - a*R*N/(R+h)
dN <- c*a*R*N/(R+h) - delta*N
return(list(c(dR, dN)))
})
}
#Pas in de regel hieronder K aan:
p <- c(r=1,K=4,a=1,c=1,delta=0.3,c=1,h=1) #parameters
s <- c(R=1,N=0.01) #begin-dichtheden van R en N
colors[1] = "blue" #optioneel, default = 'red'
colors[2] = "#FF7F50" #optioneel, default = 'blue'
par(mfrow=c(1,2)) # optioneel, maakt 2 plotjes naast elkaar
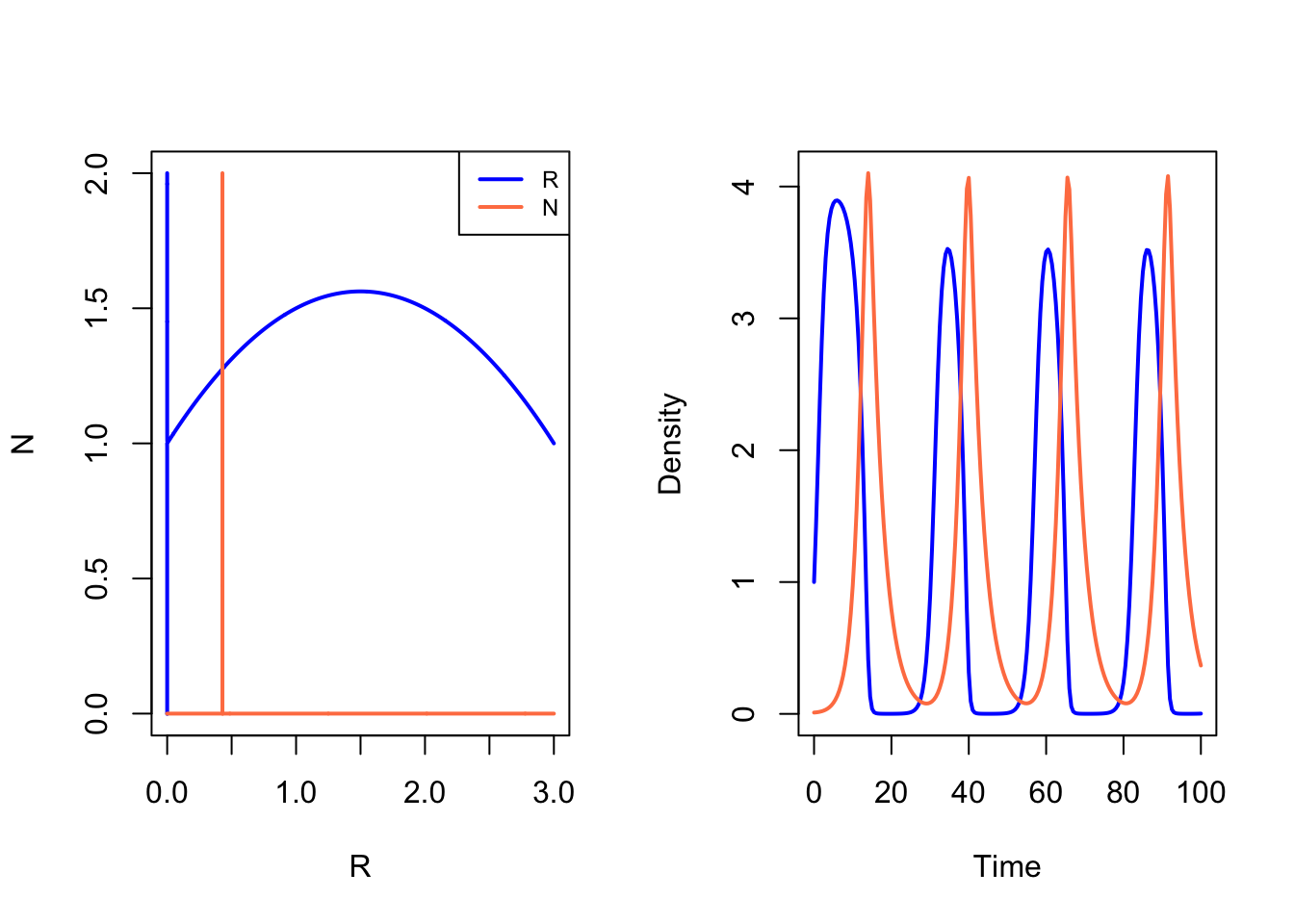
plane(xmax=3,ymax=2)
run(tstep=0.5, legend=F)
R N
0.002165465 0.366797215 Zoals verwacht verschuift het snijpunt met de x as. Hiermee verschuift natuurlijk ook de top van de parabool.
Ook bereikt de populatie geen stabiele stand meer en blijft deze enorme schommelingen maken! De volgende paragraaf gaat hier dieper op in.
Antwoorden 15 Competitie en evolutie
a. \(c_{21}\) zal groter worden. Dit kan je hier terugzien:
\[\begin{align*} \mathchoice{\frac{\mathrm{d}\textcolor{#2d43fc}{N_1}} {\mathrm{d}t}}{\mathrm{d}\textcolor{#2d43fc}{N_1}/\mathrm{d}t} {\mathrm{d}\textcolor{#2d43fc}{N_1}/\mathrm{d}t} {\mathrm{d}\textcolor{#2d43fc}{N_1}/\mathrm{d}t} = r\textcolor{#2d43fc}{N_1} (1 - c_{11}\textcolor{#2d43fc}{N_1} - c_{12} \textcolor{orange}{N_2}) \end{align*}\]
\[ \mathchoice{\frac{\mathrm{d}\textcolor{orange}{N_2}} {\mathrm{d}t}}{\mathrm{d}\textcolor{orange}{N_2}/\mathrm{d}t} {\mathrm{d}\textcolor{orange}{N_2}/\mathrm{d}t} {\mathrm{d}\textcolor{orange}{N_2}/\mathrm{d}t} = r\textcolor{orange}{N_2}\left(1 - c_{22}\textcolor{orange}{N_2} - c_{21}\textcolor{#2d43fc}{N_1}\right)\]
Als er meer competitie is, dan zal \(N_2\) steeds meer “last krijgen” van \(N_1\), dus dan neemt de populatie van \(N_2\) sterker af als de populatie van \(N_1\) toeneemt. \(c_{21}\) bepaalt hoeveel de populatiegroei van \(N_2\) verminderd, en deze zal dus groter worden.
b. De oranje lijn gaat verschuiven, omdat dit de nullcline van \(N_2\) is. De formule van deze nullcline is: \[\textcolor{orange}{N_2} = \frac{1 - c_{21}\textcolor{#2d43fc}{N_1}}{c_{22}}\] Als \(c_{21}\) toeneemt, zal de lijn stijler afnemen en het snijpunt met de x-as dus naar links verschuiven.
c. Let op: hoewel twee rechte lijnen elkaar altijd snijden als ze niet parallel lopen, zijn we als biologen alleen geïnteresseerd in snijpunten met positieve populatiegroottes. Omdat \(c_{21}\) groter wordt in dit scenario, verplaatst het snijpunt met de x-as naar links. Er komt een punt dat \(c{21}\) groter is dan \({c11}\), en de nullclines dus niet meer snijden in het positieve domein (maar nog wel ergens in een ander kwadrant).
d. Voor grote \(N_1\) en \(N_2\) hebben we nog steeds afname voor beide populaties. Als we nu over de blauwe nullcline heen gaan begint de \(N_1\) populatie juist weer toe te nemen terwijl de \(N_2\) populatie blijft dalen. We komen dan op het evenwichtspunt uit waar de \(N_2\) populatie 0 is.
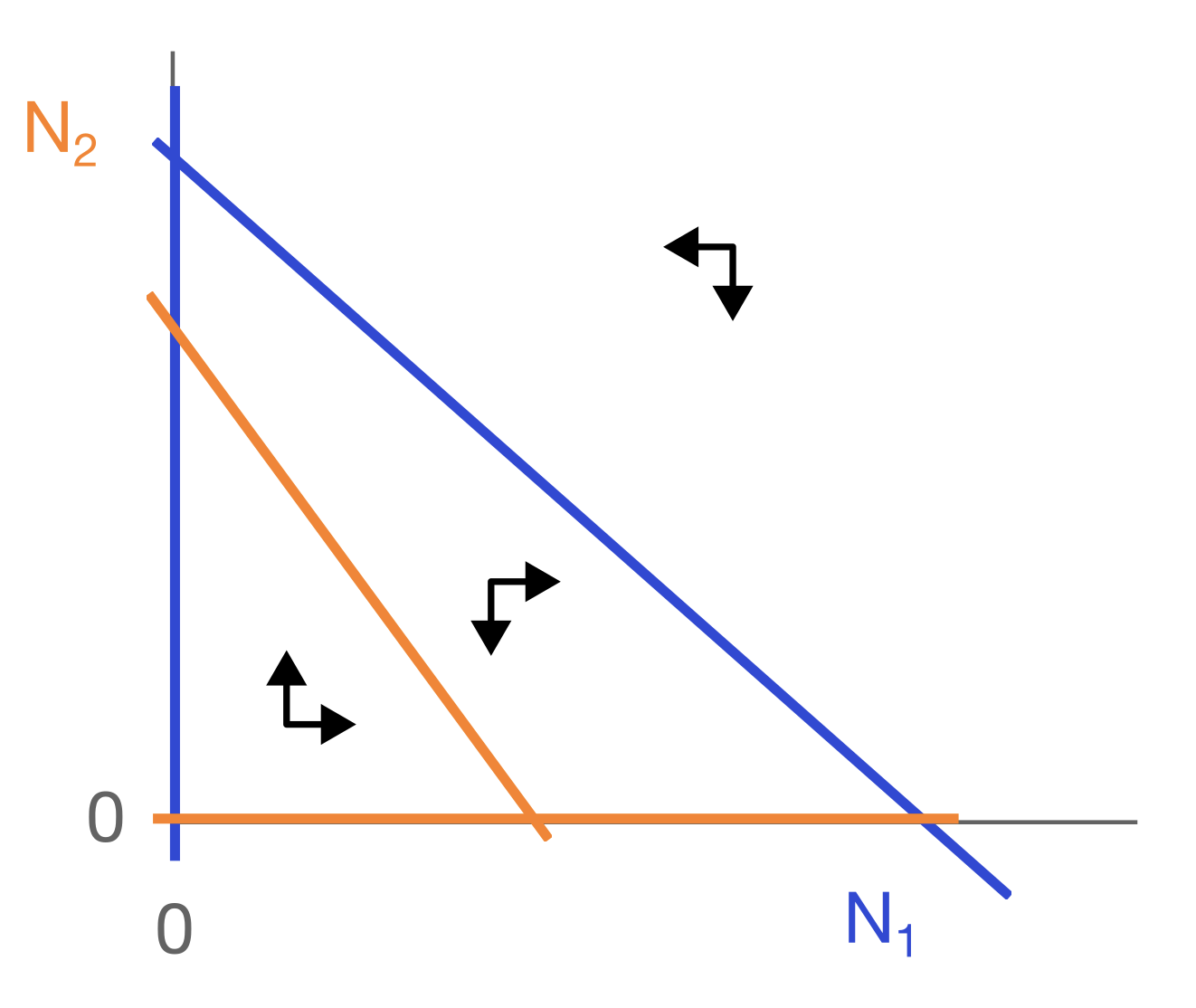
a. Je kan zien dat er een evenwicht is in het midden, waar er geen pijltjes zijn (de populaties veranderen niet meer). Als er een evenwicht ontstaat met beide populaties hebben we sterkere intraspecifieke competie.
b. Nee dat kan niet, want voor elke waarde van X en Y krijg je een specifieke hoeveelheid groei van X en Y. Je gaat dus altijd dezelfde kant op.
c. Als twee lijnen elkaar snijden zou dit betekenen dat ze op het snijpunt daarna twee verschillende kanten op gaan. Maar in b zeiden we dat op elk punt maar 1 mogelijke richting is waarin de populatie zich kan bewegen.
LET OP: je kan wel een aantal snijdende vectoren in het figuur zien, maar dit zijn niet snijpunten van de trajectories. De vectoren geven alleen aan hoe “snel” de populatie verandert in dat punt.
d. Mogelijkheid 1: Er is geen ruis in het model, maar in werkelijkheid wel.
Mogelijkheid 2: Er zijn mogelijk nog meer processen die een rol spelen in de verandering van de populaties. Hierdoor kan het lijken alsof de populaties weer op hetzelfde punt zijn beland, maar eigenlijk is de situatie toch anders waardoor ze anders kunnen reageren. Twee populaties met allebei te weinig eten zullen waarschijnlijk afnemen, maar als er meer eten wordt toegevoegd kunnen ze met dezelfde populatiegroottes mogelijk toenemen. Hier kunnen we in ons 2D systeem nog geen rekening mee houden.
Mogelijkheid 3: De tijdstap is niet continu. Zoals we in 10 Exponentiële groei zagen zorgt een te grote tijdstap er voor dat er chaotisch gedrag kan ontstaan. Mogelijk schiet de populatie te verder over een nullcline heen dan verwacht. Dit kan bijvoorbeeld gebeuren in een populatie die niet continu voortplanten, maar bijvoorbeeld maar 1 keer per jaar. Hoewel dit een goed antwoord is, neem je hiermee dus wel aan dat het universum “in stapjes” gaat, terwijl we over het algemeen aannemen dat tijd continu is.
e. Ze gaan altijd horizontaal door de nullcline van de verticale as en verticaal door de nullcline van de verticale as. Dit is zo omdat de verandering in de populatie op de verticale as 0 is als deze door de nullcline heen gaat. Hierdoor veranderd alleen de horizontale waarde en is de beweging dus horizontaal. En andersom natuurlijk voor de andere as.
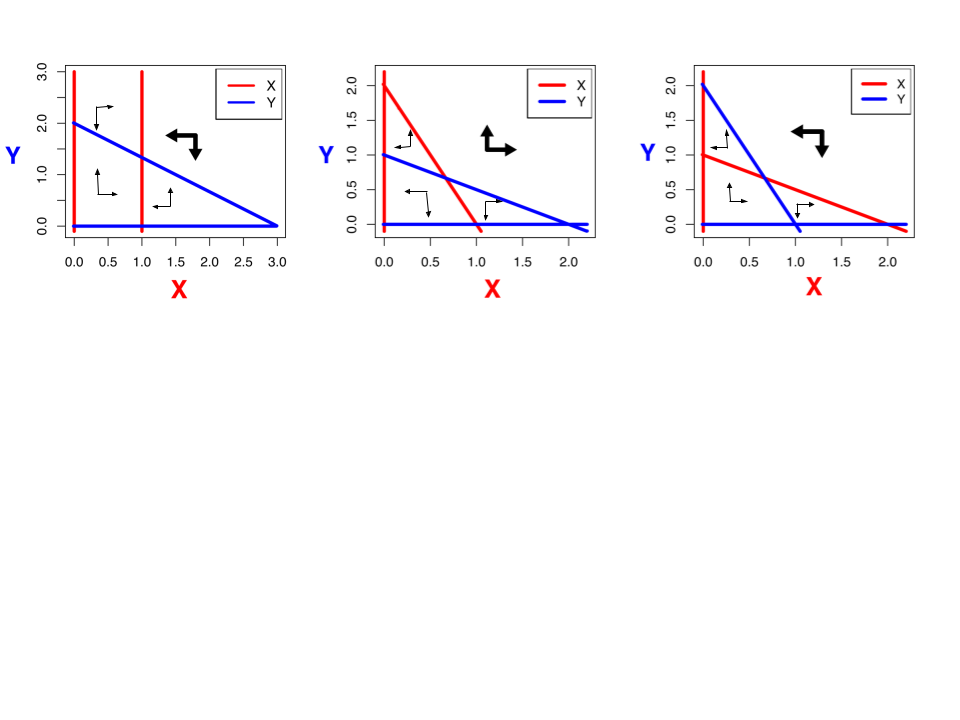
a. 
Het eerste evenwicht is stabiel, het tweede evenwicht is instabiel en het derde punt is een zadelpunt.
b.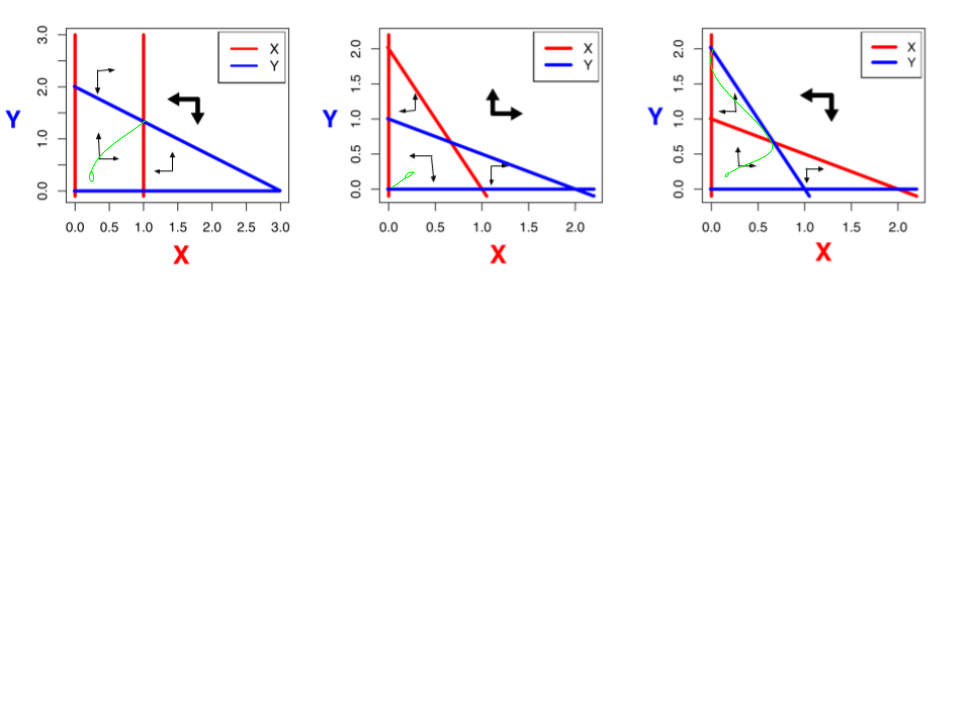 
Omdat het eerste punt stabiel is gaat de trajectorie direct righting het evenwicht. Punt 2 is instabiel en de trajectorie gaat naar de oorsprong. Punt 3 is een zadelpunt, dus de trajectorie gaat eerst richting het zadelpunt en daarna Y=2 en X=0, zoals getekend, of naar Y=0 en X=2.
c. 
a. \(C_2\) is de cheater, omdat zijn populatie toeneemt als de populatie van \(C_1\) toeneemt. \(C_2\) heeft dus voordeel van de aanwezigheid van \(C_1\) terwijl \(C_1\) dat niet heeft met \(C_2\).
b. Dit is de dichtheidsafhankelijkheid, hoe meer individuen hoe minder ze kunnen groeien. Dit is eigenlijk hoeveel individuen van beide populaites samen de omgeving kan ondersteunen. Omdat ze allebei even veel “voedsel eten” of “ruimte in beslag nemen” hebben ze allebei even veel invloed op deze factor.
Deze term zorgt dus voor competitie tussen de twee soorten. Door ze een gedeelde carrying capacity te geven kunnen we onderzoeken wanneer ze kunnen samenleven.
c.* Als we een grid van 100x100 hokjes hebben, dan zijn er in totaal 10,000 hokjes. Als deze allemaal gevuld zijn en \(C_1+C_2\) dus 10,000 is, dan moet \(1-\frac{C_1+C_2}{K}\) gelijk zijn aan 0. Want op het moment dat alle hokjes gevuld zijn moet de populatiegroei volledig gestopt zijn: \[1-\frac{C_1+C_2}{K}=0\] \[1=\frac{C_1+C_2}{K}\] \[K=C_1+C_2=10000\] K is dus gelijk aan 10,000. (Dit is niet helemaal exact omdat we de death rate \(d\) nu niet hebben meegenomen)
d. Het evenwicht met alleen cooperators is stabiel. Dit kan je zien doordat alle pijltjes er naartoe wijzen (als je ook de pijltjes in het negatieve deel wil zien zul je moeten inzoomen in de faseruimte, door plane(vector=T,grid=7,xmin=0.9,xmax=1,ymin=-0.05,ymax=0.05) te gebruiken).
Als je het zeker wil weten, kun je zoals in de vraag wordt voorgesteld het commando newton(c(C1=1,C2=0),plot=T) gebruiken. Deze tekent een zwarte punt, en print ook een tekst waarin gezegd wordt dat het punt een ‘stable node’ is.
Hetzelfde zouden we kunnen doen voor het evenwicht bij geen van beide soorten (0,0).
e. Als je met heel veel van beide soorten begint zullen beide soorten eerst afnemen en daarna zal weer alleen C1 overleven.
f. Aan het vectorveld zie je dat de pijltjes terugwijzen. Als je met heel weinig van beide soorten begint zullen beide dus uitsterven.
g. De nullclines zien er hetzelfde uit, maar zijn van plek gewisseld. Het evenwicht met alleen cooperators is nu instabiel.
h. In alle gevallen zullen beide populaties uitsterven. De cheaters groeien namelijk sneller dan de cooperators, waardoor ze de cooperators tot uitsterven drijven. Echter hebben ze de cooperators wel nodig en zullen ze daarna dus ook zelf uitsterven.
i. De enige mogelijkheid waarin beide populaties overleven is als hun groeisnelheden precies even groot zijn. Dan blijft de populatie ergens op de nullcline hangen. Dit is echter niet heel aannemelijk en een kleine verstoring zal dit “evenwicht” verbreken.
j. In het geval van de ODEs bekijken we maar 1 systeem. Met het ruimtelijke model, zijn er eigenlijk meerdere sub-populaties verdeeld over de ruimte. Als je goed kijkt is er lokaal wel sprake van dezelfde successie: cheaters nemen de boel over waarna alles uitsterft. Maar hiermee ontstaat “lege ruimte” waar weer groei in kan plaatsvinden. Cheaters kunnen echter niet in hun eentje deze lege ruimte benutten! Deze wordt in plaats daarvan uitsluitend door cooperators benut, waarna er weer een golf cheaters komt, etc.
We zagen dat bij gemengde condities in het ruimtelijke model geen coexistentie, dus we kunnen concluderen dat ruimtelijke structuur nodig is voor bovengenoemde processen.
Oefening 15.5 a. Het experiment duurde maar 18 dagen zoals te zien is in Figuur 15.5
b. De waardes die Gause (r=0.794 en K=64) had gevonden werken erg goed.
c. Ook met weinig decimalen kom je al erg ver, maar je weet dan niet per se hoe goed de fit is.
d. Dit zijn de parameters waarop R “trial and error” op uit gaat proberen, de vrije parameters. Deze zullen dus aangepast worden totdat de beste fit is gevonden.
e. De resultaten zijn nagenoeg hetzelfde met slechts kleine verschillen als je in b. een beetje goede waardes had gevonden. Dit hoeft echter niet altijd zo te zijn, omdat het regelmatig voor komt dat meerdere zeer verschillende fits mogelijk zijn op dezelfde dataset.
Antwoorden 16 Zwermen en foerageren
a. Na een tijdje is al het eten dichtbij de groep op en dan rennen de aapjes telkens terug naar het midden van de groep, waar geen eten meer is. Het wordt dan steeds moeilijker voor de appjes om eten te vinden. Als je lang genoeg wacht zie je vaak dat de aapjes toch wel weer nieuw eten vinden doordat de groep soms toevallig in de richting van het eten beweegt.
b. Zorg dat je de uitkomsten met je groepje bespreekt en dat je begrijpt wat er gebeurt.
c. Zorg dat je de uitkomsten met je groepje bespreekt en dat je begrijpt wat er gebeurt.
d. Bij een maximale eetsnelheid maakt de groep een soort pulserende bewegingen. Het lijkt erop dat ze minder fruit vinden dan de aapjes uit de eerste simulatie. Bij een minimale eetsnelheid lijkt het erop dat de aapjes meer fruit vinden. Doordat de aapjes langer aan het eten zijn beweegt de groep zich meer in één richting (de kant waar de meeste aapjes aan het eten zijn). Hierdoor kan de groep verder bewegen over het veld, en wel in de richting waar kennelijk fruit te vinden is!
e. Bewaar je antwoorden goed, deze ga je later in de cursus nog nodig hebben!
Antwoorden 17 Reacties en diffusie
a. De reactieproducten zijn de variabelen, dat zijn dus \(E\), \(S\), \(C_{ES}\) en \(P\). Deze veranderen over de tijd. De parameters zijn de evenwichtsconstantes \(k_1\), \(k_2\) en \(k_{cat}\). Deze zijn constant.
b. Er wijst maar één pijltje naar \(c_{ES}\), dus dit wordt alleen gemaakt door de combinatie van \(E\) en \(S\).
Er zijn echter ook twee pijltjes die van \(c_{ES}\) afwijzen:
- Het complex valt uit elkaar en het substraat is omgezet naar product: \(- c_{ES} \cdot k_{cat}\)
- Het complex valt uit elkaar zonder dat er product is gevormd: \(- c_{ES} \cdot k_2\)
c.
Zoals je in a/b hebt gezien komt dit neer op elk pijltje omzetten naar een wiskundige term. Bijvoorbeeld: omdat \(P\) (product) alleen een pijltje naar zich toe heeft, is er alleen een reactie waarmee deze ontstaat. De volledige ODEs zijn:
\[ \begin{align*} \mathchoice{\frac{\mathrm{d}C_{ES}} {\mathrm{d}t}}{\mathrm{d}C_{ES}/\mathrm{d}t} {\mathrm{d}C_{ES}/\mathrm{d}t} {\mathrm{d}C_{ES}/\mathrm{d}t} &= E \cdot S \cdot k_1 - c_{ES} \cdot k_2 - c_{ES} \cdot k_{cat} \\ \mathchoice{\frac{\mathrm{d}E} {\mathrm{d}t}}{\mathrm{d}E/\mathrm{d}t} {\mathrm{d}E/\mathrm{d}t} {\mathrm{d}E/\mathrm{d}t} &= c_{ES} \cdot k_2 + c_{ES} \cdot k_{cat} - E \cdot S \cdot k_1 \\ \mathchoice{\frac{\mathrm{d}S} {\mathrm{d}t}}{\mathrm{d}S/\mathrm{d}t} {\mathrm{d}S/\mathrm{d}t} {\mathrm{d}S/\mathrm{d}t} &= c_{ES} \cdot k_2 - E \cdot S \cdot k_1 \\ \mathchoice{\frac{\mathrm{d}P} {\mathrm{d}t}}{\mathrm{d}P/\mathrm{d}t} {\mathrm{d}P/\mathrm{d}t} {\mathrm{d}P/\mathrm{d}t} &= c_{ES} \cdot k_{cat} \end{align*} \]
De vermenigvuldigingstekens zou je natuurlijk weer weg kunnen laten.
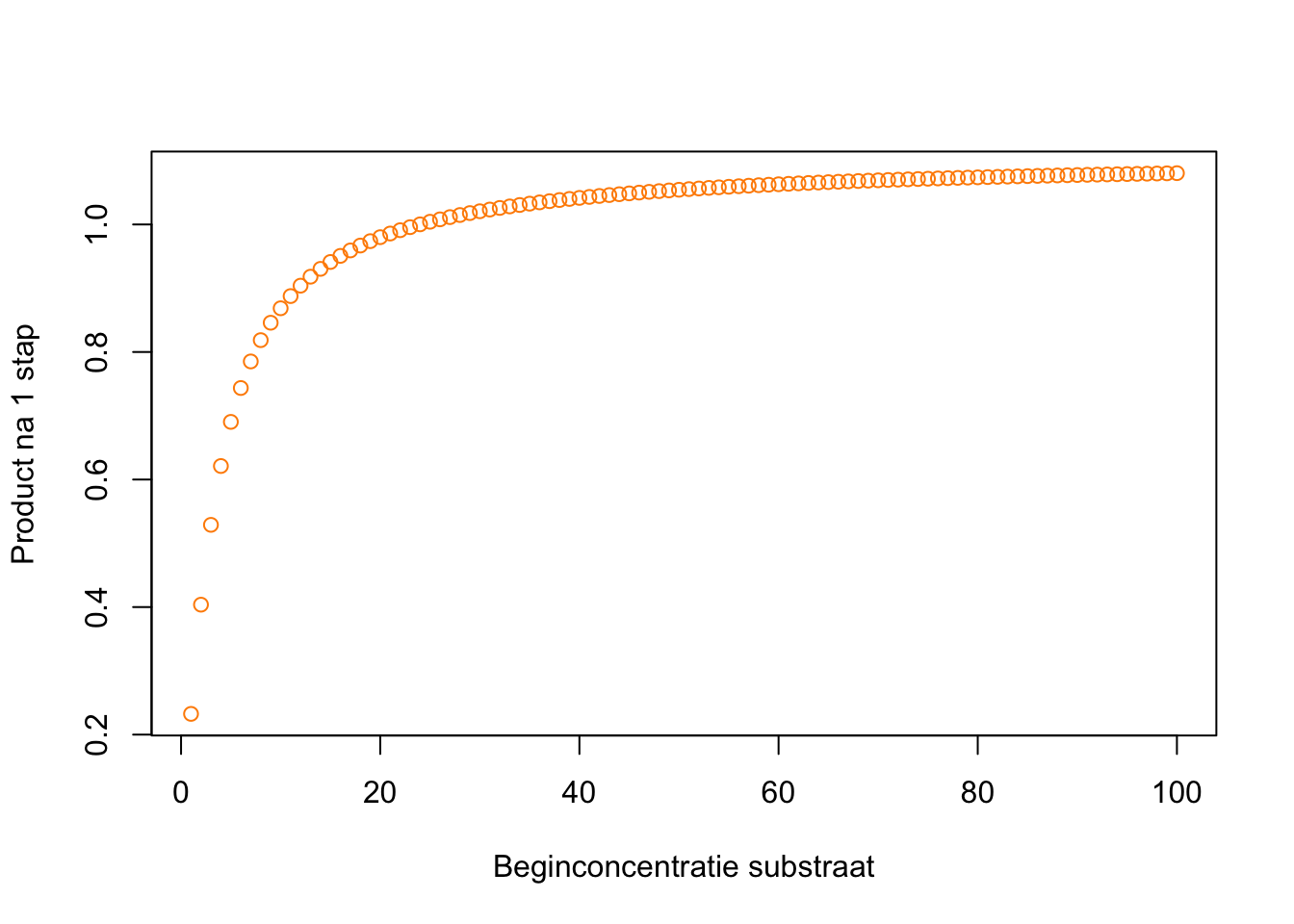
d. Als er meer substraat (\(S\)) is, kan er meer complex (\(C_{ES}\)) ontstaan, waardoor er uiteindelijk meer product gevormd wordt. Toch zijn er ook grenzen aan de hoeveelheid product die in één tijdstap gevormd kan worden. De hoeveelheid enzym verandert namelijk niet, en die is ook nodig om de vorming van het product te katalyseren. Als alle enzymen al “bezet” zijn, heeft het geen zin dat er meer substraat beschikbaar is. We verwachten dus dat de snelheid zal verzadigen. Inderdaad, als we de (initiële) reactie-snelheid voor heel veel hoeveelheden substraat berekenen, krijgen we een verzadigde curve:
source("https://tbb.bio.uu.nl/rdb/grindR/grind.R")grind.R (25-06-2024) was sourcedmodel <- function(t, state, parms) {
with(as.list(c(state,parms)), {
dE <- k2*C - k1*E*S + kcat*C
dS <- k2*C - k1*E*S
dC <- k1*E*S - kcat*C
dP <- kcat*C
return(list(c(dE, dS, dC, dP)))
})
}
prod <- c()
for(conc in seq(100)){
p <- c(k1=1,k2=0.2,kcat=1) #Parameters
s <- c(E=1,S=conc,C=0,P=0) #Starting population sizes
stapje <- run(tmax=1,ymax=3,tstep=1,timeplot=F)
prod[conc] <- stapje["P"]
}
plot(y = prod, x = seq(100), col = colors[4], xlab = "Beginconcentratie substraat", ylab = "Product na 1 stap")
a.
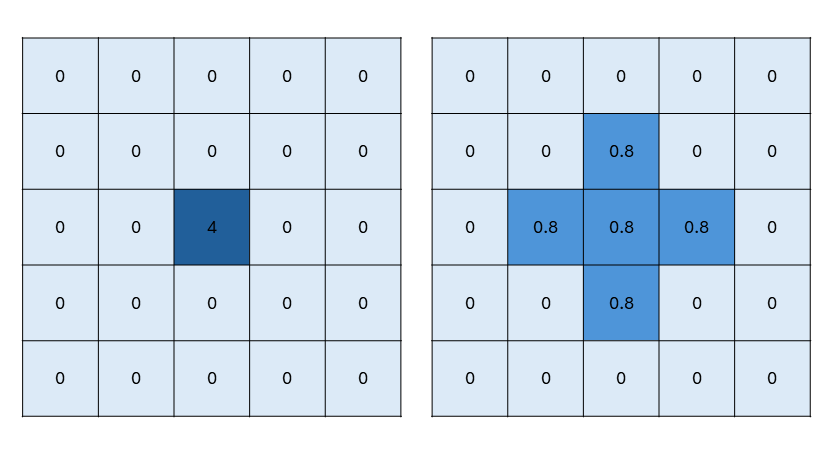
b.
Zelfs met een hoge diffusiesnelheid kan een stofje per stap maar één hokje opschuiven. We zouden dit bereik kunnen vergroten zodat stofjes sneller diffunderen. Een andere (eenvoudige) oplossing is om meerdere diffusiestappen in één minuut te doen, zodat het stofje meer kan verspreiden. Dit betekent dus dat je kleinere tijdstapjes maakt.
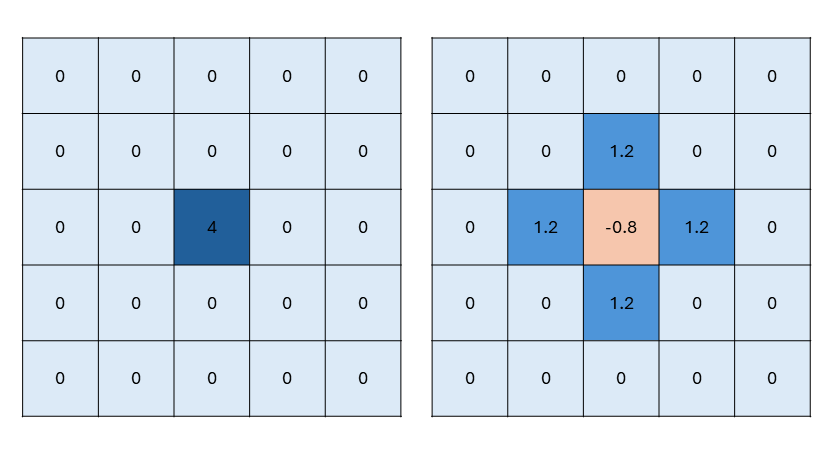
c. Dit probleem hebben we eerder gezien bij populatiegroei met differentievergelijkingen. Destijds zagen we dat de discrete tijdstappen van differentievergelijkingen soms voor problemen kunnen zorgen. Dit kon worden opgelost door het gebruiken van ODEs, met continue tijd (=oneindig kleine tijdstapjes).
Nu zien we eenzelfde soort probleem, maar dan in de ruimte in plaats van met tijd. Doordat we de de ruimte opdelen in hokjes kunnen we “voorbij het evenwicht schieten”, zoals je in vraag a hebt gezien. Dit probleem kan opgelost worden met behulp van PDEs. PDEs hebben niet alleen continue tijd, maar ook continue ruimte. Hierdoor kunnen ze nooit voorbij een evenwicht schieten, ook als we de diffusieconstante heel hoog maken.
PDEs zijn dus voor diffusie in hokjes wat ODEs zijn voor differentievergelijkingen.
a.
De bacteriën bevinden zich eerst in één enkele kolonie, waarna ze zich opsplitsen in kleinere groepen. De schadelijke metabolieten diffunderen rondom de bacteriën (afhankelijk van de gekozen radius). Het is ongunstig voor de bacteriën om in hele grote groepen te leven, omdat er dan heel veel bacteriën in de groep last hebben van de toxiciteit.
Dit lijkt erg op het systeem van Turing-patronen. De gekozen namen parameter-namen in de modelomschrijving (\(a\) en \(i\)) zijn dan ook geen toeval: deze staan voor ‘activator’ en ‘inhibitor’. Het activerende process is reproductie van bacteriën, die lokaal de ‘concentratie’ verhoogt. Het inhiberende process is de toxiciteit. Dit inhiberende process wordt bepaald binnen een grotere radius, zoals bij de Turing patronen de inhibitor meer diffundeerde (en zo een hogere ‘radius’ heeft!). Hierdoor krijg je een “vlekkenpatroon” van verschillende groepjes bacteriën.
b.
De radii van birth/toxiciteit zijn vergelijkbaar met hogere/lagere diffusiesnelheid van de activator en inhibitor. Inderdaad, als je de radii gelijk maakt, ontstaat er geen patroon en blijft er alleen het (willekeurige) diffusieproces over.
c. Doordat er meerdere groepjes bacteriën zijn ontstaan, kan een virus niet gemakkelijk overspringen naar de andere groepen. Hierdoor is het onwaarschijnlijk dat alle individuen besmet worden.
d. De andere groepjes kunnen zich uitbreiden in de richting van weggehaalde groepjes. Vaak zie je daarbij dat ze zich “vanzelf” weer opsplitsen. Na een verstoring zullen er dus dankzij zelf-organistatie keer op keer ongeveer hetzelfde aantal groepjes ontstaan!
a. Differentiaalvergelijkingen (ODEs): De grootte van de bacteriepopulaties kan prima als continu worden beschouwd, omdat er heel veel individuen zijn (het verschil tussen 1 miljoen en 1 miljoen en een half, is niet belangrijk). Er is ook geen ruimtelijk patroon omdat de Erlenmeyer gemengt is. De populaties delen alle voedselbronnen, dus groei kan goed met een gedeelde carrying capacity (\(1-\frac{N_1+N_2}{K}\)) gemodelleerd worden.
b.
Reactie-diffusie systeem (PDE): Er zijn ruimtelijke patronen, dus we moeten zeker voor een ruimtelijk model gaan. Omdat het hier om concentraties gaat (en niet discrete individuen met birth/death processen) is een reactie-diffusie systeem een goed modelformalisme.
c.
Individual based model (IBM):
Er is een ruimtelijk patroon met individuen (planten). Omdat er sprake is van “bezette” en “onbezette” plekjes, is een grid de meest eenvoudige manier om dit te bestuderen. Echter zou je ook kunnen kiezen voor een continue ruimte, waarbij je binnen een radius bekijkt of de ruimte ‘vol’ is.
d. Differentiaalvergelijkingen (ODEs):
Hoewel in het hoofdstuk staat dat zelfs de oceaan niet altijd goed gemengd is, geeft deze modelomschrijving duidelijk aan dat dit hierbij wel het geval is. We hoeven dus eigenlijk geen ruimtelijk model te gebruiken. Zoöplankton deelt zich constant (en niet 1 keer per week/maand/jaar), dus is continue tijd geschikt. We gebruiken daarom niet een differentievergelijking, maar ODEs.
e.
Reactie-diffusie systeem (PDE):
We willen hier een ruimtelijk patroon bestuderen. Als het gaat om individuele cellen zouden we een grof grid kunnen gebruiken. Als de stoffen echter ook door de extracellulaire matrix diffunderen, kunnen er misschien fijnere patronen ontstaan en moet een veel fijner grid (of een ‘echte’ PDE!) gebruikt worden.
f.
ODE of individual based model:
We zouden een ODE kunnen gebruiken met verschillende vergelijkingen voor elke kleur konijnen. Er kan echter een probleem ontstaan op het moment dat de konijnen- en/of havikkenpopulatie(s) erg klein worden (zie ?nte-atto). Een individual based model is computationeel waarschijnlijk langzamer, maar kan wel voorkomen dat we hele gekke (en onwaarschijnlijke) resultaten krijgen als er hele kleine populaties zijn.
g.
Individual based model:
De bacteriën groeien op een agarplaat, dus om het systeem goed weer te geven zou een ruimtelijk model het meest geschikt zijn. Gemuteerde bacteriën delen dan lokaal en kunnen zo zorgen voor een lokaal groepje gemuteerde bacteriën. Vaak worden deze systemen op een grid gemodelleerd, maar meer moderne simulaties gebruiken biofysische modellen met continue ruimte, waarbij cellen elkaar weg kunnen duwen (cell shoving).
h.
Reactie-diffusie systeem (PDE):
Het morfogen diffundeert, dus die zou het best met continue ruimte (of in ieder geval kleine hokjes) gemodelleerd kunnen worden. De individuele cellen zouden eventueel wel discreet gemodelleerd kunnen worden (al dan niet op een grid).
i.
ODE:
De paracetamol bevindt zich in het bloed, waarvan we over het algemeen aannemen dat het goed gemengd wordt. Ook hoeven we ons bij moleculaire concentraties niet druk te maken over individuele verschillen en is het modelleren van de dichtheid paracetamol een goed genoege benadering.
j.
Reactie-diffusie systemen (PDEs):
We hebben een ruimtelijk model nodig, en we hebben te maken met concentraties. Daarom zijn reactie-diffusie systemen het meest geschikt. De individuele calcium-atomen gaan we natuurlijk niet modelleren.
k.
Individual based model (IBM):
Het is belangrijk om de zeehonden en orca’s als individuen weer te geven, omdat ze elk een andere kant op zullen bewegen. Daarnaast is er een ruimtelijk patroon, doordat de zeehonden vanuit verschillende hoeken worden belaagd.
Antwoorden 18 Exciteerbare media
a. We hebben dit concept vaker terug zien komen, bijvoorbeeld in Oefening 13.3 over sexuele reproductie. Hier zagen we een vergelijkbaar faseportret waar met kleine dichtheden geen groei mogelijk is, met grotere dichtheden wel groei mogelijk is, en met nóg grotere dichtheden de groei weer daalt. Hierdoor zagen we logistische groei, maar dan met wat “opstartproblemen”. Hoewel het Fitzhugh-Nagumo model natuurlijk geen populatiegroei beschrijft, is het principe hetzelfde.
b.
a=-0.2
func <- function(V){
return(-V * (V-a) * (V-1))
}
curve(func,-0.3,1.15,lwd=2,ylim=c(-0.1,0.2),
ylab="",xlab="V",col="seagreen")
axis(1, labels = FALSE,lwd=2) # x-axis
axis(2, labels = FALSE,lwd=2) # x-axis
abline(h=0,lty=1,col="black")
abline(v=1,lty=3,col="grey")
abline(v=a,lty=3,col="grey")
Nu is de functie positief vanaf \(V=0\), dus vanaf die waarde verwachten we activatie van een actiepotentiaal.
c.
Deze is super makkelijk: je hoeft alleen de min in een =-teken te veranderen:
\[\begin{align*} \mathchoice{\frac{\mathrm{d}V} {\mathrm{d}t}}{\mathrm{d}V/\mathrm{d}t} {\mathrm{d}V/\mathrm{d}t} {\mathrm{d}V/\mathrm{d}t} = -V(V-a)(V-1) - W &= 0 \quad \text{ als...}\\ W &= -V(V-a)(V-1)\\ \end{align*}\]
d.
Het is dezelfde curve als in vraag b! (nogmaals, als we oplossen voor \(W\) hoeven we deze alleen maar aan de andere kant van het = teken te zetten)
a=-0.2
func <- function(V){
return(-V * (V-a) * (V-1))
}
curve(func,-0.3,1.15,lwd=2,ylim=c(-0.1,0.2),
ylab="W",xlab="V",col="seagreen")
axis(1, labels = FALSE,lwd=2) # x-axis
axis(2, labels = FALSE,lwd=2) # x-axis
abline(h=0,lty=1,col="black")
abline(v=1,lty=3,col="grey")
abline(v=a,lty=3,col="grey")
e.
\[\begin{align*} \mathchoice{\frac{\mathrm{d}W} {\mathrm{d}t}}{\mathrm{d}W/\mathrm{d}t} {\mathrm{d}W/\mathrm{d}t} {\mathrm{d}W/\mathrm{d}t} = \epsilon(V-bW) &= 0 \quad \text{ als...}\\ V - bW &= 0\\ bW &= V\\ W &= \frac{V}{b}\\ \end{align*}\]
# source the grind script
source("https://tbb.bio.uu.nl/rdb/grindR/grind.R")
# define the model-function so grind can use it
model <- function(t, state, parms) {
with(as.list(c(state,parms)), {
dV <- -V*(V-a)*(V-1) - W # dV/dt
dW <- e*(V- b*W) # dW/dt
return(list(c(dV,dW)))
})
}
# initial values of V and W (a bit above rest potential)
s <- c(V=0.2,W=0)
p <- c(e=0.001,b=1,a=-0.2)
par(mfrow=c(1,2))
plane(xmin=-0.3,ymin=-0.05,ymax=0.2,xmax=1.05,portrait=F,vector=T,grid=3)
newton(plot=T)
run(tmax=5000)
f. Er is nu nog maar één evenwicht, en de pijlen wijzen er niet meer naar toe, dus het is een instabiel evenwicht (Grind.R bevestigd dit ook). Er is dus ook geen ‘drempelwaarde’ meer, omdat er geen stabiel evenwicht (rustpotentiaal) is. In plaats daarvan blijft dit systeem oscilleren.
g. De sinusknoop van het hart zou een voorbeeld kunnen zijn. De sinusknoop genereert continu actiepotentialen.
a. Elke 250 tijdstappen ontstaat er een nieuwe golf in de ‘sinusknoop’ (hokje linksboven). Er is dus elke 250e tijdstap een hartslag.
b. Als we op de ‘boe-knop’ drukken zien we dat er ruis ontstaat: er vormt zich een actiepotentiaal tussen twee golven in. Hierdoor zijn er soms twee hartslagen kort na elkaar, of is de tijd tussen twee hartslagen juist wat langer. Er is echter geen blijvend effect: na een korte tijd is het hartritme weer stabiel.
c. Het tekenen van een lijn door een golf heen zorgt ervoor dat de golf een spiraal vormt (zoals we in 18.5 Ophopingen, blokkades, en spiralen zagen). Hierdoor wordt het hartritme versneld, wat een blijvend effect is.
d. Het herstellen van het ritme door delen van de golf weg te halen met de muis is erg moeilijk en zorgt voor alleen maar meer spiralen.
De ‘Clear!’ knop daarentegen werkt een stuk beter, omdat hiermee het hele hart in één keer geactiveerd wordt. Dit zorgt ervoor dat het hele hart refractair is (dat betekent dat er dus tijdelijk geen actiepotentiaal gevormd kan worden). Na deze refractaire periode kan het hart weer normaal gaan kloppen met het ritme van de sinusknoop (linksboven).
a. Er gebeurt niks, omdat iedereen in het dorp nog immuun is. Ze zijn tenslotte kortgeleden nog geïnfecteerd!
b. Als we alle vatbare individuen tegelijkertijd infecteren, zijn er hierna geen vatbare individuen meer over, waardoor de ziekte zich niet verder kan verspreiden. Het zou dus inderdaad een succesvolle methode kunnen zijn. Aan de andere kant is het natuurlijk niet heel ethisch verantwoord om allemaal mensen moedwillig te infecteren met dit virus.
c. Als er genoeg mensen gevaccineerd zijn (30% of hoger) kan de infectie zich niet snel genoeg verspreiden om (veel) ongevaccineerde mensen te bereiken. Er zijn dan namelijk maar weinig vatbare individuen in de buurt.
d. Als de vaccinatiegraad hoog genoeg is (30% of hoger) zal de ongevaccineerde toerist waarschijnlijk niet geïnfecteerd worden. Hoewel er kleine lokale uitbraken kunnen zijn, wordt dit nooit endemisch. Bij een lagere vaccinatiegraad is er echter wel een risico voor de ongevaccineerde toerist, want er kunnen constante golven in het dorp blijven rondgaan!
e. Echt populatie mensen bewegen ook nog veel. Hierdoor krijgt een infectie meer kans om zich te verspreiden dan in deze enorm versimpelde simulatie!
a. Er zit veel variatie in de fractie afgebrande bomen. Meestal is het ergens tussen de 1% en 20%. Als je de simulatie vaak genoeg afspeelt zul je ook gevallen tegenkomen waarbij een veel groter deel van de bomen afbrandt. Dit kan gebeuren doordat bomen rondom de brandhaard toevallig allemaal dicht bij elkaar staan.
b. Bij een dichtheid van 0.2 en 0.3 brandt er telkens maar een hele kleine fractie van de bomen af. Er is weinig variatie. Bij een bomen-dichtheid van 0.5 branden bijna alle bomen af, al blijven er vaak een paar kleine eilandjes van bomen ongedeerd. Ook bij deze aantallen is er weinig variatie. Bij een bomen-dichtheid van 0.6 zie je dat eigenlijk alles altijd afbrand (met eventueel een heel klein eilandje van gelukkige bomen).
c.
Code
a=0.4
n=8
func <- function(V){
return(V^n / (a^n + V^n))
}
curve(func,0,1,lwd=2,ylim=0:1,
ylab="afgebrande fractie",xlab="V",col="seagreen")
De fractie afgebrand bos zou er per bomen-dichtheid ongeveer zo uit kunnen zien. Voor lage dichtheden brandt er bijna geen bos af, dan is er een punt (in dit geval rond de 0.4) waarbij de fractie afgebrand bos heel variabel is, en voor hogere dichtheden brandt bijna het gehele bos af.
d. Het is een goed idee om de bomen-dichtheid niet te hoog te laten worden. Een klein verschil in dichtheid (0.4 en 0.5 bijvoorbeeld) kan al een heel groot verschil maken voor de fractie afgebrand bos. Daarnaast zou je bijvoorbeeld een strook met wat minder bomen kunnen gebruiken om het verspreiden van de bosbrand te voorkomen (waar in het hoofdstuk hebben we eerder zoiets gezien?).
e. Dan kan er, nadat dit een tijdje onmogelijk was, in dat gebied weer een nieuwe ‘golf’ van bosbranden ontstaan. Met andere woorden: het bos wordt een exciteerbaar medium!
f. Juist als bomen zich snel voortplanten, is brand een groter probleem. Er komen dan telkens nieuwe bomen bij, die weer in de brand kunnen vliegen doordat de brand nog niet weg is uit dat gebied. Als de bomen zich heel langzaam voortplanten is de brand al uit dat gebied verdwenen (er waren immers geen bomen meer over) voordat er nieuwe bomen ontstaan. Zo heeft de bosbrand niet genoeg ‘vatbaar’ weefsel meer om te ‘infecteren’ (lees: geen bomen om te verbranden). Op die manier kan de brand zelfs helemaal weg gaan als bomen zich langzaam genoeg voortplanten!