8 Afgeleiden
8.1 Introductie
De afgeleide van een functie beschrijft hoe steil de functie is, oftewel wat de richtingscoëfficiënt is. Een rechte lijn met de vorm \(y=ax+b\) heeft voor elke \(x\)-waarde dezelfde richtingscoëfficiënt (\(a\)). We kunnen daarom zeggen dat de afgeleide van \(y=ax+b\) gelijk is aan een constante waarde, namelijk \(y=a\). De afgeleide vertelt iets over hoe snel \(y\) verandert: hoe hoger de richtingscoëfficiënt (\(a\)), hoe sneller \(y\) stijgt of daalt.
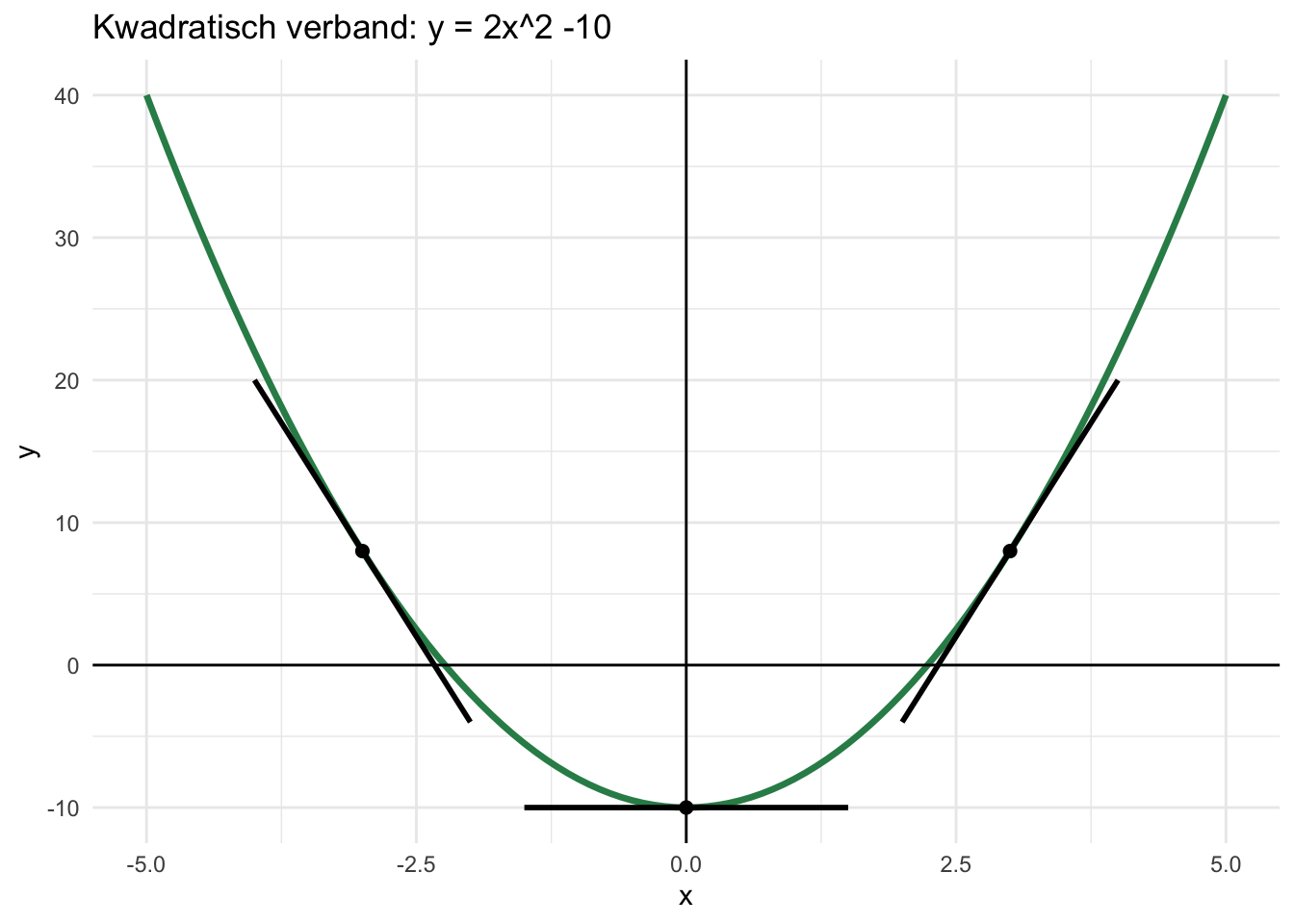
De afgeleide van een lineaire vergelijking is dus een constante waarde die niet verandert voor verschillende \(x\)-waarden. Voor de meeste (meer biologisch interessante) vergelijkingen is dit echter niet het geval. Dit betekent dat de afgeleide een functie is van \(x\). Met andere woorden: de grafiek heeft niet voor elke \(x\)-waarde dezelfde richtingscoëfficiënt. Neem bijvoorbeeld de vergelijking \(y = x^2 - 10\):
De richtingscoëfficiënt varieert veel voor verschillende \(x\)-waarden: de grafiek daalt eerst voor \(x<0\), loopt dan even horizontaal voor \(x=0\), en stijgt steeds sneller voor \(x>0\). Met andere woorden: de afgeleide is negatief voor lage waarde van \(x\), en positief voor positieve waarden van \(x\). Als de afgeleide gelijk is aan \(0\), weten we dat de functie een piek of een dal heeft.
De afgeleide van \(f(x)\) schrijven we als \(f'(x)\). Als \(f(x)\) de positie van een fiets geeft, geeft \(f'(x)\) de snelheid van de fiets. Eventueel kunnen we ook van deze snelheid \(f'(x)\) de afgeleide bepalen, die wordt geschreven als \(f''(x)\). Deze staat dan voor de versnelling van de fiets. Omdat biologische processen vaak omschreven worden in termen van snelheden, is het belangrijk om begrip te hebben van wat afgeleiden precies zijn. De meest voorkomende rekenregels leer je door ermee te oefenen vanzelf uit je hoofd, maar het is niet nodig om alle regels uit je hoofd te weten. Bij de toets kun je specifieke rekenregels altijd even nagaan met behulp van één van de spiekbriefjes.
8.2 Afgeleiden van veel voorkomende vergelijkingen
| Functie | Afgeleide | \(f(x)\) | \(f'(x)\) |
|---|---|---|---|
| \(a\) | \(0\) | \(6\) | \(0\) |
| \(ax\) | \(a\) | \(7x\) | \(7\) |
| \(ax^b\) | \(b \cdot a x^{b-1}\) | \(8x^3\) | \(24x^2\) |
| \(c \cdot f(x)\) | \(c \cdot f'(x)\) | \(2x^{13}\) | \(2 \cdot 13x^{12} = 26x^{12}\) |
| \(f(x) + g(x)\) | \(f'(x) + g'(x)\) | \(x^4 + 4x\) | \(4x^3 + 4\) |
| \(a^x\) | \(a^x \cdot ln(a)\) | \(2^x\) | \(2^x \cdot ln(2)\) |
| \(e^x\) | \(e^x\) | \(e^x\) | \(e^x\) |
| \(a e^{bx}\) | \(b \cdot a e^{bx}\) | \(\frac{1}{2} \cdot \pi \sqrt{2} \cdot e^{2x}\) | \(\pi \sqrt{2} \cdot e^{2x}\) |
| \(e^{f(x)}\) | \(f'(x) \cdot e^{f(x)}\) | \(e^{2x^2 - x}\) | \((4x - 1) \cdot e^{2x^2 - x}\) |
| \(a^{f(x)}\) | \(\ln(a) \cdot f'(x) \cdot a^{f(x)}\) | \(5^{4x - 1}\) | \(\ln(5) \cdot 4 \cdot 5^{4x - 1}\) |
| \(\ln(x)\) | \(\frac{1}{x}\) | \(\ln(x)\) | \(\frac{1}{x}\) |
| \(\ln(a x) = \ln(a) + \ln(x)\) | \(\frac{1}{x}\) | \(\ln(4x) = \ln(4) + \ln(x)\) | \(\frac{1}{x}\) |
| \(f(x) \cdot g(x)\) | \(f'(x) \cdot g(x) + f(x) \cdot g'(x)\) | \((x^2 - 4)(x^3 + 2x + 3)\) | \(5x^4 - 6x^2 + 6x - 8\) |
| \(\frac{f(x)}{g(x)}\) | \(\frac{g(x) \cdot f'(x) - f(x) \cdot g'(x)}{(g(x))^2}\) | \(\frac{4x + 1}{x^2 + 1}\) | \(\frac{-4x^2 - 2x + 4}{(x^2 + 1)^2}\) |
8.3 Opdrachten
Oefening 8.1
Bereken de afgeleide van de volgende functies:
a. \(f(x)=x^2+15x\)
b. \(f(x)=12x^5-6\)
c. \(f(x)=\frac{7}{x^4}\)
d. \(f(x)=ax^3-bx^5\)
Oefening 8.2
Bekijk de hierboven gegeven tabel met afgeleiden van veel voorkomende vergelijkingen. Leg in je eigen woorden uit waarom het nuttig kan zijn om exponentiële groei op te schrijven met grondtal \(e\) (het getal van Euler die ongeveer gelijk is aan 2.71828, niet te verwarren met e die in R staat voor ‘exponent’).