19 Inleiding: Waarom (bio)statistiek?
19.1 Omgaan met onzekere gegevens
Meten is weten, toch? Helaas is het in de praktijk niet zo simpel. Gegevens zijn namelijk zelden exact. Metingen hebben afwijkingen, steekproeven zijn vaak niet representatief en meestal speelt toeval een rol. Het is daarom lang niet altijd gemakkelijk om gegevens te interpreteren.
Zowel binnen de wetenschap als daarbuiten moeten we dus kunnen omgaan met onzekerheid in gegevens. Statistiek is de wetenschap van methoden en technieken die ons helpen om verantwoorde conclusies te trekken uit onzekere gegevens. In deze cursus maak je kennis met dit uitgebreide vakgebied.
19.2 Statistiek en data science zijn onmisbaar in biologisch onderzoek
De ontwikkeling van de statistiek als vakgebied is historisch nauw verweven met de biologie. Pioniers als Ronald A. Fisher, Karl Pearson en Francis Galton ontwikkelden hun statistische concepten en methoden oorspronkelijk om biologische vragen te beantwoorden.
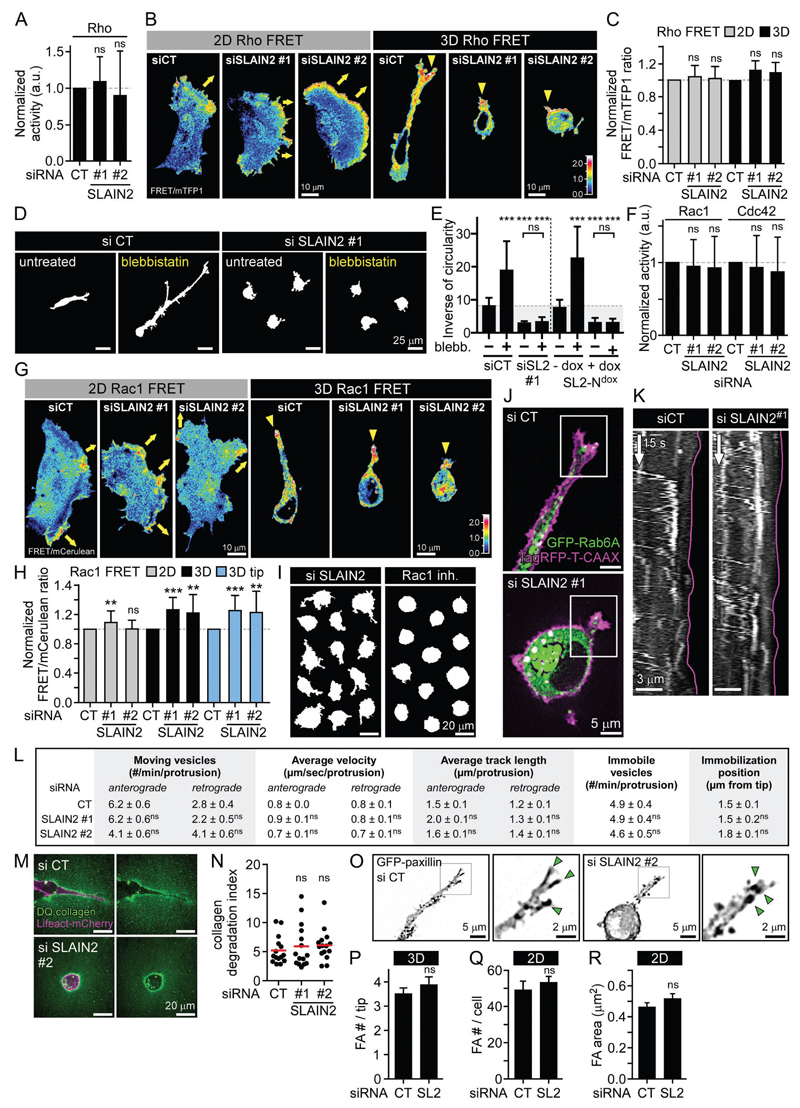
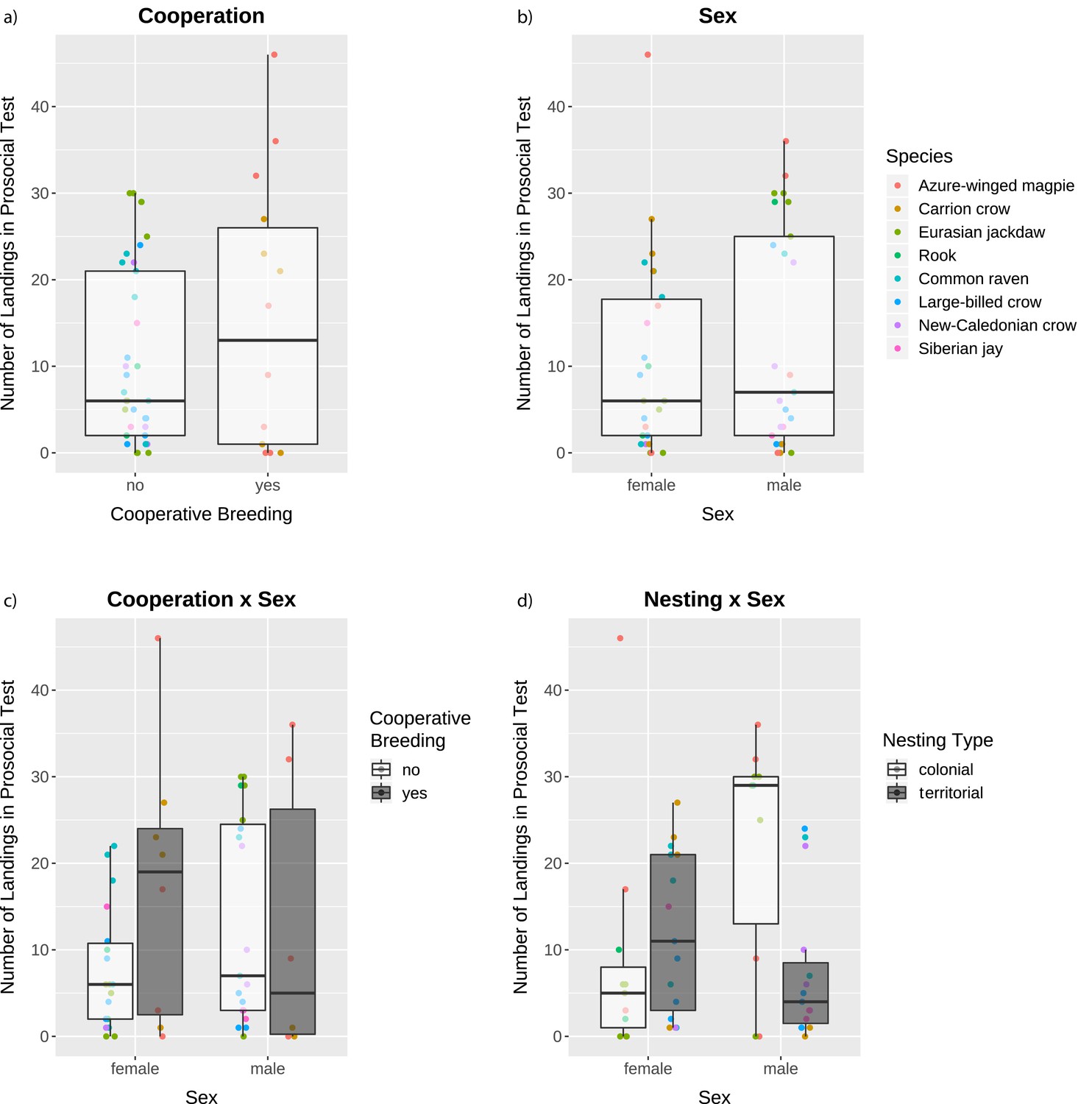
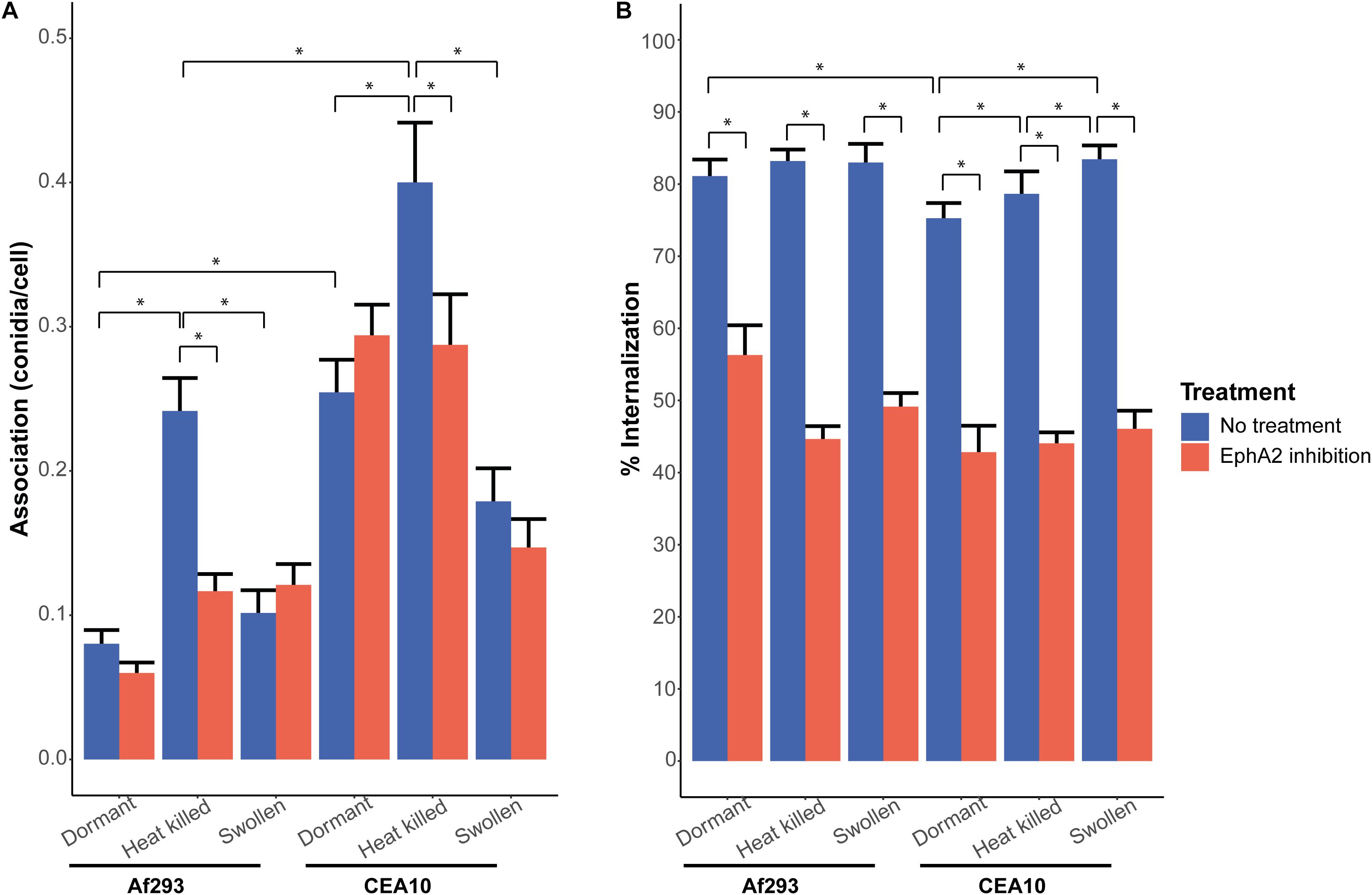
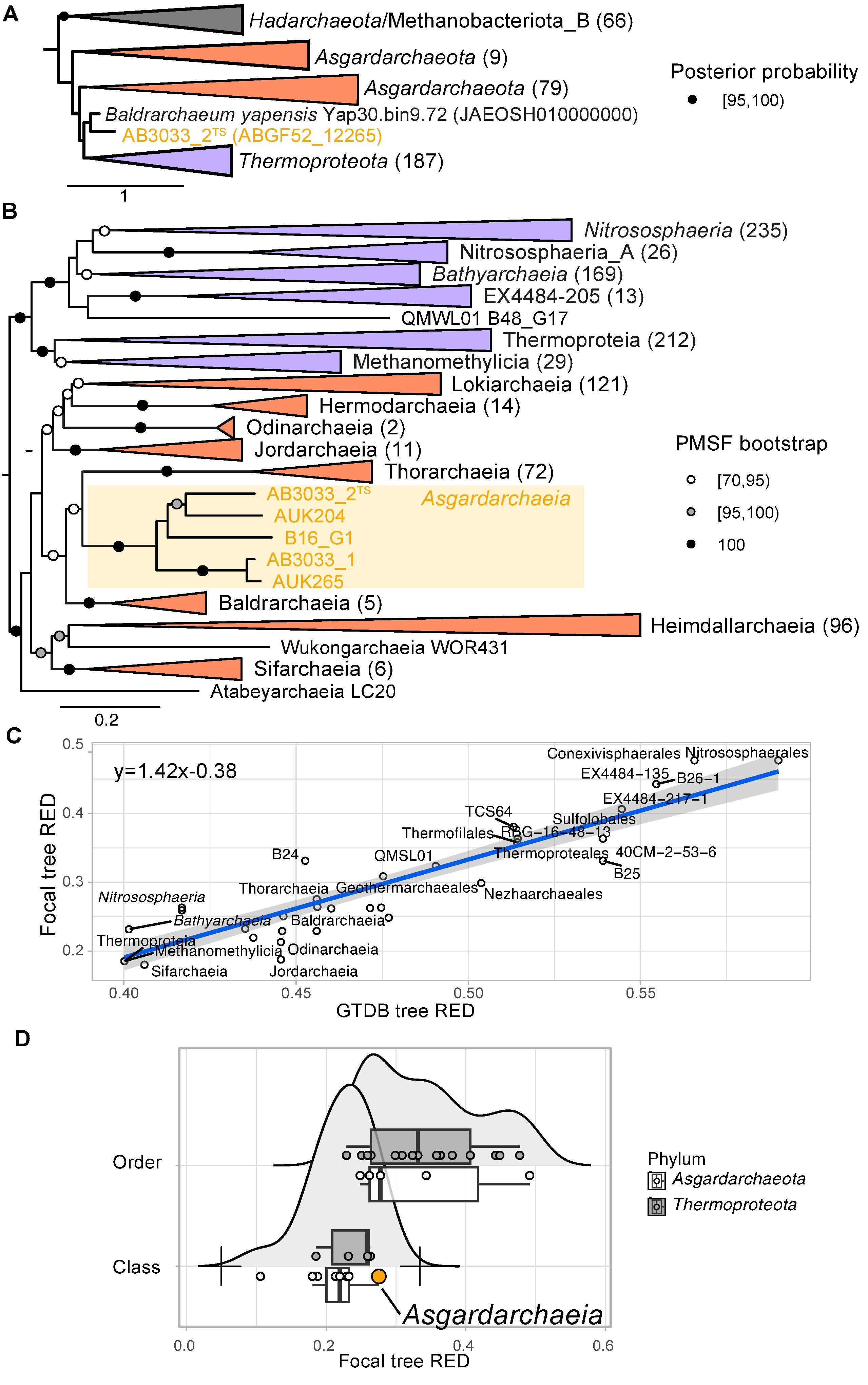
Tegenwoordig behoort statistiek tot het standaardgereedschap van elke bioloog, ongeacht het deelgebied. Figuur 19.1 laat dat zien: het toont figuren uit artikelen die recent zijn gepubliceerd door verschillende onderzoeksgroepen van ons departement. Kwantitatieve data-analyse en statistiek spelen in al die artikelen een belangrijke rol.
19.3 Statistiek en data science in wetenschap en samenleving
Ook buiten de biologie kom je overal statistische resultaten tegen. De technieken die binnen de biologie in gebruik zijn, worden net zo goed toegepast binnen andere wetenschapsgebieden, zoals psychologie of economie. Kennis van statistiek is dan ook een essentiële academische vaardigheid.
Maar het belang van statistiek stopt niet bij de muren van de universiteit. Voor veel bedrijven zijn statistische methoden en data-analyse cruciaal. Zij vertrouwen bijvoorbeeld op statistiek om de vraag naar producten te voorspellen, voorraden te optimaliseren, of prijzen te bepalen. Ook de overheid en politiek kunnen niet zonder. Hoe zouden we de corona-pandemie zijn doorgekomen zonder schattingen van \(R_0\), voorspellingen van het aantal ziekenhuisopnames, en analyses van de effecten van maatregelen? Hoe zou het stikstofdebat eruit zien zonder statistische modellen? Hoe zouden verkiezingen verlopen zonder peilingen? Ook als kritische burger heb je dus baat bij kennis van statistiek.
19.4 Over dit deel van het cursusboek
Er zijn veel goede boeken beschikbaar over (bio)statistiek, zowel gedrukt als online. Toch hebben we ervoor gekozen om zelf een cursusboek te schrijven. Dat heeft verschillende redenen.
Ten eerste hebben we in deze cursus alleen tijd voor korte introductie. Een op maat gemaakt eigen cursusboek kan de stof efficiënter aanbieden dan een bestaand boek dat bedoeld is voor een veel langere cursus. We voelen ons ook bezwaard om je een dik boek te laten kopen en daar maar een klein deel van te behandelen.
Ten tweede willen we graag laten zien dat de verschillende onderdelen van de cursus Biologische modellen en Statistiek niet los van elkaar staan: bij statistiek zullen basiswiskunde, programmeren in R en het denken in termen van modellen weer van pas komen.
Ten derde hebben we met een eigen cursusboek zelf in de hand welke stof we willen behandelen en welke nuances we aanbrengen. In een paar keuzes wijken we af van de meeste boeken die speciaal voor biologen geschreven zijn. Hieronder noemen we er een paar.
Statistiek is een modelleervak
Eerder in deze cursus heb je je verdiept in theoretische modellen. Je hebt geleerd dat een model een vereenvoudigde beschrijving is van een aspect van de echte wereld, gebaseerd op aannames. Zulke aannames zijn strikt genomen zelden waar en de conclusies op basis van een model zijn alleen betrouwbaar als de aannames geschikt zijn voor de toepassing.
In de statistiek is het net zo. Om conclusies te trekken uit onzekere gegevens zul je altijd aannames moeten maken over de werkelijkheid; zowel over de manier waarop de gegevens tot stand zijn gekomen als over de onderliggende biologie. In andere woorden, statistische resultaten zijn altijd gebaseerd op een statistisch model (statistical model). Het is belangrijk om dat model zorgvuldig te kiezen, want je conclusies vallen of staan met je aannames. Dat geldt net zozeer voor statistische modellen die we gebruiken om gegevens te interpreteren als voor dynamische modellen over, zeg, predatoren en hun prooi.
Voor statistici is dit allemaal vanzelfsprekend. Maar in leerboeken bedoeld voor andere vakgebieden wordt dit zelden benadrukt. In dit boek proberen we dat wel te doen.
Hypothesetoetsen als besluitprocedures
In Hoofdstuk 25 en Hoofdstuk 26 zul je leren over hypothesetoetsen. Traditioneel worden hypothesetoetsen gepresenteerd als besluitprocedures: procedures om te besluiten of bepaalde hypotheses moeten worden verworpen. Hoewel besluitprocedures belangrijk zijn, is het in de wetenschap niet altijd verstandig, laat staan noodzakelijk, om een binair besluit te forceren over de status van een hypothese. In werkelijkheid zijn de beschikbare gegevens vaak te verenigen met verschillende hypotheses; een mechanische besluitprocedure staat dan in de weg van een genuanceerde blik.
De gebruikelijke presentatie suggereert bovendien dat je een hypothese kunt beoordelen enkel op basis van de huidige dataset—alsof voorkennis er niet toe doet. Dat is absurd, maar veel leerboeken suggereren, onbedoeld misschien, iets anders. In dit boek zullen we daarom minder nadruk leggen op binaire conclusies.
Subtiele redeneerfouten en statistical literacy
Redeneren over onzekere gegevens is niet makkelijk, en sommige subtiele redeneerfouten kom je keer op keer tegen, in het dagelijks leven, het publieke debat, en de wetenschap. Een belangrijk doel van deze cursus is dan ook om ervoor te zorgen dat jij deze fouten zelf niet meer maakt en ze kunt herkennen en benoemen. We geven dit soort conceptueel inzicht en statistical literacy in dit boek veel nadruk.
19.5 Statistiek is leuk!
Misschien zie je op tegen dit onderdeel van de cursus. Veel studenten verwachten dat statistiek moeilijk en saai zal zijn.
Dat valt best mee. Veel studenten geven achteraf aan dat de stof veel interessanter was dan ze vooraf hadden gedacht. Bovendien zul je merken dat je investering zich uitbetaalt: na deze cursus zul je je veel minder gemakkelijk laten misleiden door misinformatie vanuit de media, de wetenschap, en de politiek.
19.6 Terminologie
Hieronder volgt een korte lijst met de belangrijkste termen uit dit hoofdstuk. Omdat het belangrijk is om de Engelse terminologie te kennen, geven we bij elk begrip ook de Engelse vertaling. In de tekst zelf voegen we de Engelse vertaling van begrippen soms ook tussen haakjes toe.
| Nederlands | Engels | Beschrijving |
|---|---|---|
| statistiek | statistics | De wetenschap van methoden en technieken om verantwoorde conclusies te trekken uit onzekere gegevens. |
| hypothese | hypothesis | Een veronderstelling die door onderzoek mogelijk ontkracht of bevestigd kan worden. |
| meetfout | measurement error | Het verschil tussen het resultaat van een meting en de daadwerkelijke waarde van de variabele. |
Let op het verschil tussen probability en chance. De beste vertaling voor het Nederlandse woord kans is bijna altijd probability, omdat chance ook wordt gebruikt voor toeval, mogelijkheid of gelegenheid:
He found the key by chance.
If you try hard, you have a chance.
I’ll give you one more chance to fix your mistakes.
Bouchet et al. Developmental Cell 39, no. 6 (2016): 708–23↩︎
Horn et al. eLife (October 2020)↩︎
Grace et al. Nature 529, no. 7586 (2016): 390–93↩︎
Keizer et al. Frontiers in Microbiology 11 (2020)↩︎
Tamarit et al Systematic and Applied Microbiology 47, no. 4 (July 1, 2024)↩︎
de Greef et al Science Advances 10, no. 30 (July 24, 2024)↩︎