Mini-project

Belangrijke informatie over je verslag

Hieronder staat waar je verslag van het mini-project (de samenwerkingsopdracht) aan moet voldoen:

  • Je verslag moet puntsgewijs (a=…, b=…, etc.) antwoord geven op de gestelde vragen.
  • Gebruik volzinnen in het beantwoorden van de vragen, waaruit blijkt op welke vraag je antwoord geeft. Zo volgt het vanzelf een logisch verhaal.
  • Je verslag moet een korte conclusie bevatten waarin je de belangrijkste inzichten uit dit project samenvat (dit is de laatste subvraag).
  • Bij je verslag, moet je ook het samenwerkingsstartformulier inleveren. Zonder dit formulier kun je geen voldoende krijgen.

Efficiënte konijnen

We bestuderen in een ecosysteem de hoeveelheid gras (\(G\)) en konijnen (\(R\)). We nemen aan dat gras logistisch groeit, en wordt opgegeten door konijnen. Konijnen gebruiken een fractie \(c\) van het gegeten gras om nieuwe konijnen-biomassa te maken. Hoewel de waarden van deze parameter (en de andere parameters) niet in het veld gemeten is, kunnen we met een model wel onderzoeken wat er gebeurt als deze parameter verandert. Zo kunnen we biologische inzichten vergaren.

Hieronder staat het model beschreven in grind.

source("https://tbb.bio.uu.nl/rdb/grindR/grind.R")

# Grind model
model <- function(t, state, parms) {
  with(as.list(c(state,parms)), {
    dG <- b*G*(1 - G/K) - d*G - a*G*R/(G+h)
    dR <- c*a*G*R/(G+h) - delta*R
    return(list(c(dG, dR)))
  })
}

# Parameters (p-vector) en beginwaarden (s-vector)
p <- c(  
  b = 1,       # groeisnelheid gras
  d = 0.2,     # natuurlijke sterfte/afbraak gras 
  K = 10,      # draagkracht gras 
  a = 10,      # graas-snelheid 
  c = 0.024,   # conversie-efficiëntie 
  delta = 0.2, # sterfte konijnen 
  h = 2        # halfverzadiging 
)

s <- c(G = 1, R = 1)  # beginwaarden (gras, konijnen)

colors[1] <- "darkseagreen"
colors[2] <- "brown"
par(mfrow=c(1,2))

plane(xmax=15, ymax=0.3, main="Faseruimte (x-as: G, y-as: R)")
run(legend=TRUE, main="Tijdreeksen van G en R", xlab="Tijd", tmax=200, tstep=0.25)

  1. Schrijf de ODEs uit het bovenstaande Grind-model op in standaard wiskundige notatie (dus niet in R-code). Geef hierbij met accolades (zoals in Vergelijking 14.1) kort aan wat elke term in de ODEs betekent.

  2. Leg uit waar alle parameters (\(b\), \(K\), \(d\), \(a\), \(h\), \(c\), en \(\delta\)) voor staan.

  3. Bepaal in welke eenheden de parameter \(a\) wordt uitgedrukt (let op: hill-functies hebben geen eenheden, en kun je daarom meteen wegstrepen).

  4. Welke waarde van \(c\) verwacht je intuïtief dat het gunstigst is voor de konijnenpopulatie?

  5. Bereken de nullclines van dit systeem.

  6. Waar liggen de nullclines voor de konijnen als \(ca=\delta\)? Leg je antwoord uit in biologische begrippen.

  7. Schets met pen en papier1 de nullclines in een faseruimte (x-as: gras, y-as: konijnen). Varieer hierbij de waarde van \(c\) zodat er drie kwalitatief verschillende scenario’s ontstaan (laag, midden, hoog). Geef aan of licht tekstueel toe waarom de nullclines deze vorm / ligging hebben.

  8. Gebruik de eerder gegeven grind code (met de gegeven parameters) om te onderzoeken bij welke waarden van \(c\) de scenario’s uit g optreden. Tussen welke waarden van \(c\) ontstaan er stabiele populaties?

  9. Stel ook eens zeer hoge waarden in voor \(c\) (bijvoorbeeld 0.5 of 0.8). Wat gebeurt er in deze gevallen? (hint: het kan zijn dat je de tijdstapgroote \(tstep\) een stuk kleiner in moet stellen). Leg je antwoord uit in biologische termen.

  10. Heroverweeg je antwoord op d in het licht van je bevindingen in h en i.

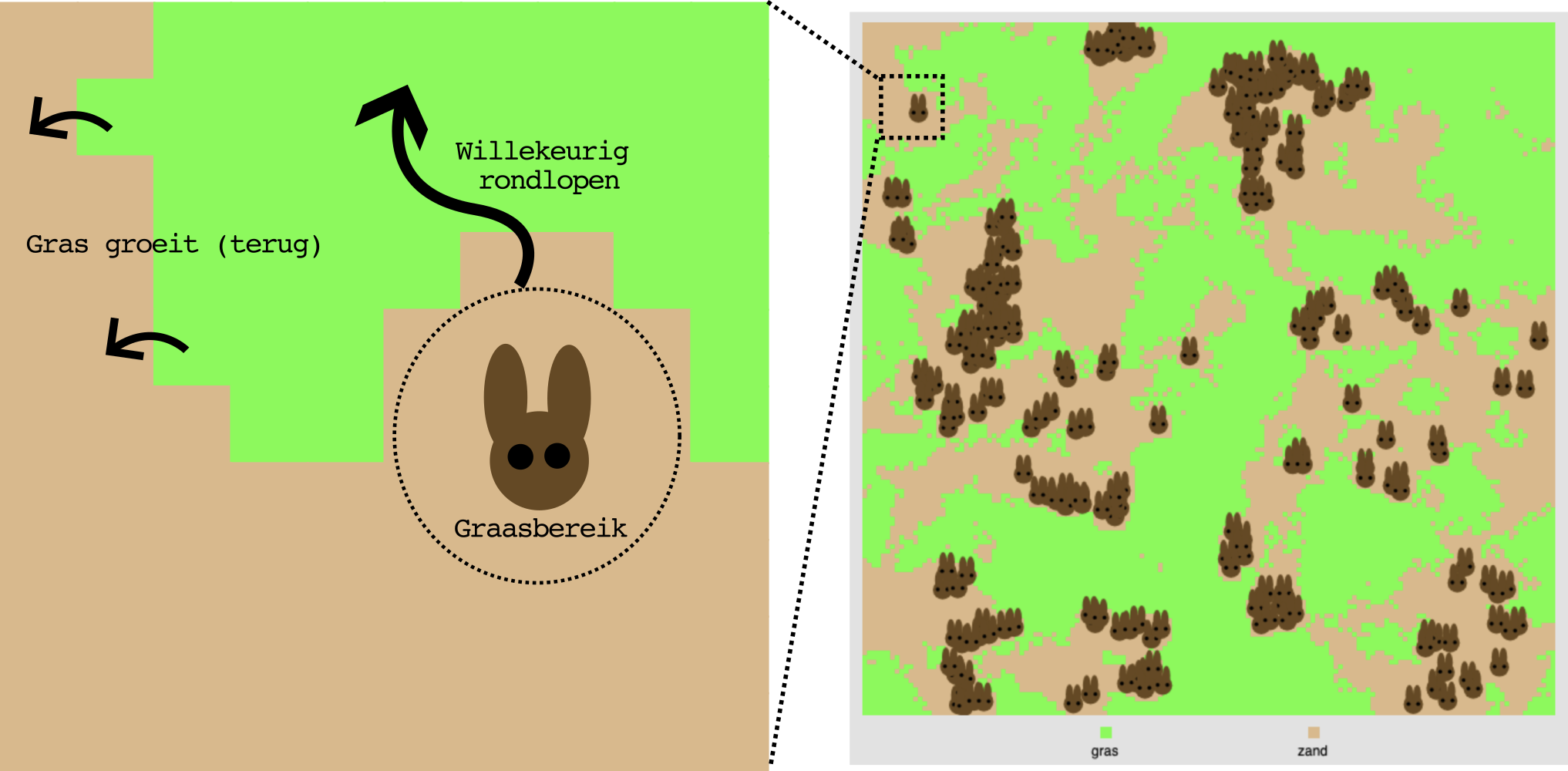
Nu we het effect van \(c\) in het wiskundige model begrijpen, gaan we een simulatie bekijken waarbij de konijnen zich fysiek in een (ruimtelijk) grasveld bevinden (zie link en cartoon hieronder).

Online simulatie van konijnen die gras eten: https://tbb.bio.uu.nl/bvd/simulations/konijnen/

Online simulatie van konijnen die gras eten: https://tbb.bio.uu.nl/bvd/simulations/konijnen/

In deze versimpelde simulatie bewegen de konijnen zich over een rasterwereld:

  • Groene vakjes stellen gras voor.
  • Lichtbruine vakjes stellen kale grond voor (geen gras).
  • Gras kan lokaal weer aangroeien op kale vakjes met een constante snelheid, waardoor de graspopulatie zichzelf kan onderhouden.
  • In tegenstelling tot het ODE-model heeft gras hier geen natuurlijke sterfte.

Konijnen bewegen willekeurig rond. Alle konijnen eten al het gras binnen een bepaalde straal onmiddellijk op (je weet hoe ze zijn, gekke knijnen). Een vaste fractie (c) van elk opgegeten grasvakje wordt omgezet in nieuwe biomassa. Wanneer deze 1 bereikt, plant het konijn zich voort en verschijnt er een nieuw konijn vlakbij het huidige konijn. Dan moet het konijn opnieuw gras gaan eten om weer nieuwe konijnen te kunnen maken.

Konijnen sterven met een constante kans per tijdseenheid. Deze sterftekans hangt niet af van de hoeveelheid gras, net zoals in het ODE-model.

De grafiek in de simulatie toont alleen de laatste 500 tijdstappen, zodat de dynamiek duidelijker zichtbaar is.

  1. Gebruik de simulatie om te bestuderen wat het effect is van de \(c\) parameter in dit nieuwe model. Zie je iets wat in het ODE model niet gebeurde?

  2. De simulatie heeft een vinkje om de konijnen en het gras elke tijdstap te “mengen” (door ze op willekeurige plekken te zetten). Zet deze knop aan en bestudeer nogmaals wat het effect is van de \(c\) parameter.

  3. Bekijk ook de volgende simulatie: https://tbb.bio.uu.nl/bvd/simulations/konijnen_competition/ van bruine konijnen, en witte konijnen met een conversie-efficiëntie die 50% hoger is. Omschrijf in je eigen woorden wat je ziet.

  4. Schrijf een korte conclusie over dit project (~200 woorden).

  1. je mag gewoon een foto hiervan in je verslag zetten↩︎