# Installeer de packages (hoeft maar 1 keer!)
install.packages(c("FME", "deSolve","coda","rootSolve"))ODEs modelleren in R
In 14 Predator-prooi interacties hebben we een heel beroemd model uit de biologie geanalyseerd: het Lotka-Volterra predator-prooi model. Dit model gaat natuurlijk niet specifiek over konijnen en vossen, maar zou op allerlei systemen toegepast kunnen worden: bacteriofagen die bacteriën infecteren, protozoa die bacteriën eten, lieveheersbeestjes die bladluizen eten, vleermuizen die motjes eten, etc. Naast het predator-prooi model bestaat er ook het Lotka-Volterra competitie model (waar we in het volgende hoofdstuk naar gaan kijken). Zodoende is het Lotka-Volterra model uitgegroeid tot één van de meest veelzijdige modellen in de biologie, waarmee voorspellingen gedaan kunnen worden over welke soorten wel/niet kunnen samenleven.
We hebben gezien hoe met behulp van faseruimtes het relatief eenvoudig kan zijn om inzicht in een biologisch proces te vergaren. Maar de eenvoud van deze eerdere analyses is deels te verklaren door de eenvoud van het model dat we hebben gebruikt. Hoe meer interacties we willen begrijpen, hoe moeilijker het zal worden om met pen en papier te werk te gaan. Daarom gaan we leren om ODEs door te rekenen met het Rscript grind.R, waarmee je eenvoudig faseruimtes en grafiekjes van de dynamica van variabelen kan plotten.
Leerdoelen
Misschien is het je opgevallen dat dit hoofdstuk geen nummer heeft. Dit hoofdstuk is inhoudelijk namelijk wat korter, en is vooral bedoeld om kennis te maken met het R-script grind.R. De overige leerdoelen zijn:
- Begrijpen hoe een simpel model (zoals het Lotka-Volterra model) kan worden uitgebreid door extra details toe te voegen (bijvoorbeeld een predator die verzadigd raakt).
- Een Hill-functie herkennen, en de kenmerken kunnen benoemen (initiële helling, half-waarde, maximum).
- R kunnen gebruiken om faseruimtes met nullclines en trajectories te tekenen, en de daarbij horende oplossingen.
De verzadigde predator
In ons eerdere Lotka-Volterra model namen we aan dat predatie lineair proportioneel is aan de dichtheden van de predator en prooi. Dit deden we door gebruik te maken van een simpele predatieterm: \(aRN\). Mede dankzij deze eenvoud waren de nullclines zo eenvoudig: een stel rechte lijnen waarvan het makkelijk te bepalen is waar/of ze snijden. Echter heeft deze eenvoud ook zijn beperkingen. Dit lineaire verband betekent dat per predator (ookwel: per capita) in totaal \(aR\) prooi gegeten kan worden (nogmaals, “per” kun je lezen als “gedeeld door”, dus \(\frac{aRN}{N} = aR\)). Bij oneindig hoge prooidichtheden, kan elke predator dus oneindig veel prooi eten. In het echt zal een predator eigenlijk een tijd bezig zijn met het verwerken en verteren van de prooi. Zodoende zal de predatie-term bij hele hoge prooi-dichtheden eigenlijk moeten verzadigen. Om dit te bestuderen met ons model, zouden we de predatie-term aan kunnen passen:
\[\begin{align*} \frac{\mathrm{d}\color{#2a53f7}R}{\mathrm{d}t} &= \underbrace{b(1-\frac{\color{#2a53f7}R}{K})\color{#2a53f7}R}_{\text{geboorte prooi}} - \underbrace{d\color{#2a53f7}R}_{\text{sterfte prooi}} - \underbrace{\frac{\color{black}a\color{#2a53f7}R\color{orange}N}{h+\color{#2a53f7}R}}_{\text{nieuwe predatieterm}}\\ \frac{\mathrm{d}\color{orange}N}{\mathrm{d}t} &= \underbrace{\frac{ca\color{#2a53f7}R\color{orange}N}{h+\color{#2a53f7}R\color{black}}}_{\text{geboorte predator}} - \underbrace{\delta \color{orange}N}_{\text{sterfte predator}} \end{align*}\]
Wat is met deze nieuwe predator-term de per capita predatie? Dat wil zeggen: hoeveel prooi kan een enkele predator per tijdseenheid opeten? Hiervoor delen we wederom de predatie-term door \(N\), waardoor we functie \(\frac{aR}{h+R}\) krijgen. Deze functie wordt de functionele respons van de predator genoemd. Om een beeld van deze functie te krijgen, is het handig om deze even te schetsen.
Vorm van de nieuwe predatieterm
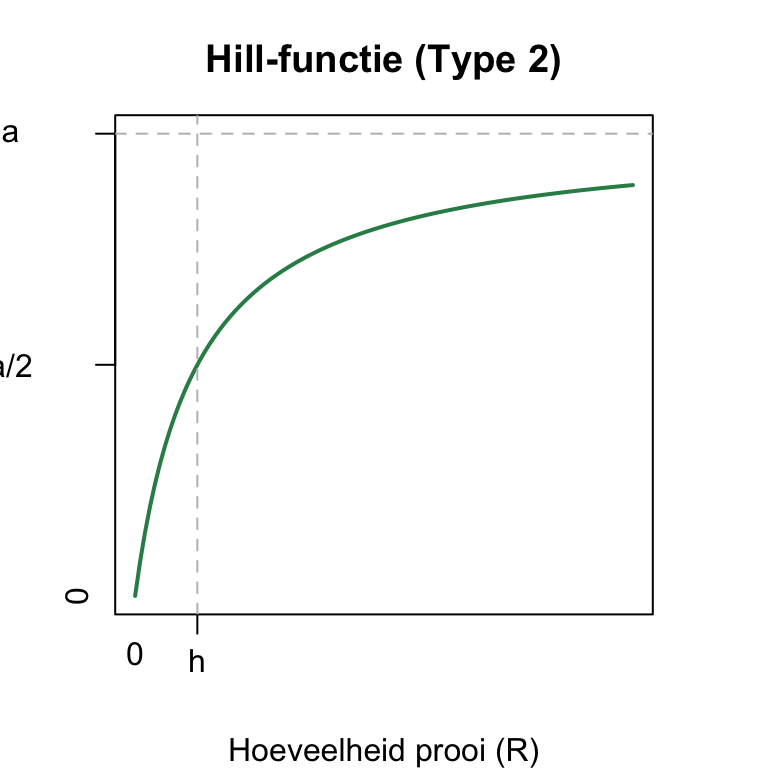
Laten we eerst even naar de noemer te kijken, en vooral naar de balans tussen \(h\) en \(R\). Als \(R\) heel klein is, heeft \(h\) de overhand in de noemer, waardoor \(R\) verwaarloosbaar is. Dus voor kleine \(R\) nadert de functie \(\frac{aR}{h}\), wat een lineaire toename is. Dus voor kleine prooi-dichtheden, neemt predatie lineair toe met de prooi-dichtheid, net zoals in het eerdere model. Maar als \(R\) alsmaar groter wordt, wordt \(h\) juist verwaarloosbaar ten opzichte van \(R\). Daarom nadert deze functie bij hoge \(R\) de waarde \(\frac{aR}{R} = a\). Dus: zelfs bij hele hoge prooidichtheden kan een enkele predator per tijdseenheid (bijv. per dag) hoogstens \(a\) prooi eten. Tussen deze twee extreme waarden zit nog een laatste bijzondere punt: het punt waar \(R\) precies gelijk is aan \(h\). Op dit punt is de functie gelijk aan \(\frac{aR}{R+R}=\frac{aR}{2R}=\frac{a}{2}\). De parameter \(h\) geeft dus de prooi-dichtheid waar de predatieterm half-maximaal is. Nu kunnen we de functie schetsen, zoals weergegeven in Figuur 1 (a).
Hill-functies
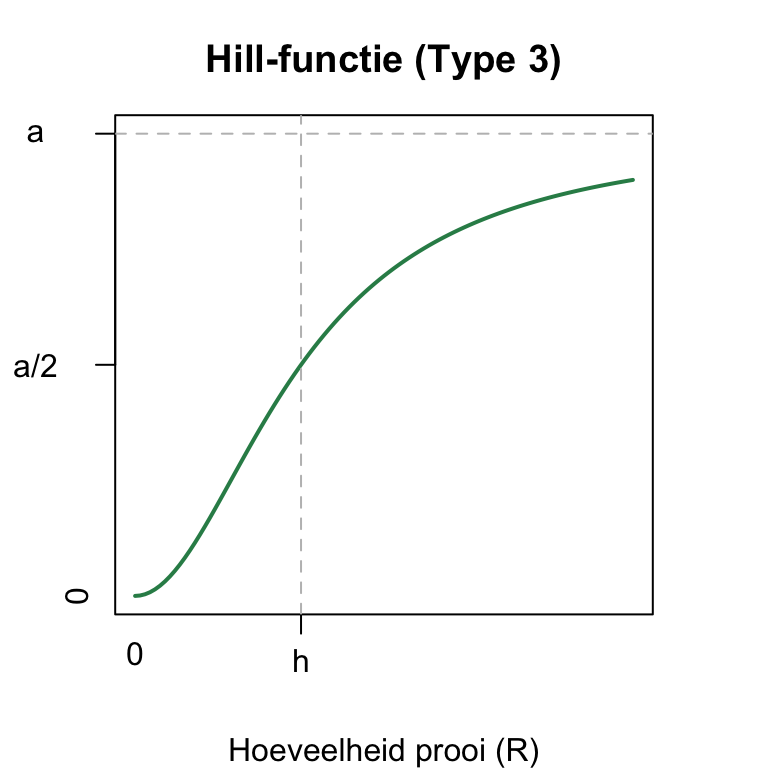
Functies van deze vorm worden “Hill-functies” genoemd (vernoemd naar Archibald Hill, niet naar het feit dat het een soort heuveltje is). Met een kleine aanpassing aan deze Hill-functie (\(\frac{aR^2}{h^2+R^2}\)), kun je deze respons ook sigmoïde (S-vormig) laten verlopen (Figuur 1 (b)).
Code
a=1
h=1
par(mar=c(4,3,3,3))
func <- function(x){
return(a*x/(x+h))
}
curve(func,0,8,lwd=2,ylim=c(0,1.), xaxt="n", yaxt="n",
ylab="Predatie",xlab="Hoeveelheid prooi (R)",col="seagreen",
main="Hill-functie (Type 2)")
axis(1, labels = FALSE, at=c(h)) # x-axis
axis(2, labels = FALSE, at=c(0.5,1.0)) # x-axis
abline(h=a,lty=2,col="grey")
abline(v=h,lty=2,col="grey")
mtext("h",side=1,at=h,line=0.7)
mtext("0",side=1,line=0.5,at=0)
mtext("0",side=2,line=0.5,at=0)
text(-2.0,1,"a",xpd=NA)
text(-2.0,0.5,"a/2",xpd=NA)
func <- function(x){
return(a*x^2/(x^2+h^2))
}
curve(func,0,3,lwd=2,ylim=c(0,1.), xaxt="n", yaxt="n",
ylab="Predatie",xlab="Hoeveelheid prooi (R)",col="seagreen",
main="Hill-functie (Type 3)")
axis(1, labels = FALSE, at=c(h)) # x-axis
axis(2, labels = FALSE, at=c(0.5,1.0)) # x-axis
abline(h=a,lty=2,col="grey")
abline(v=h,lty=2,col="grey")
mtext("h",side=1,at=h,line=0.7)
mtext("0",side=1,line=0.5,at=0)
mtext("0",side=2,line=0.5,at=0)
text(-0.6,1,"a",xpd=NA)
text(-0.6,0.5,"a/2",xpd=NA)Nu we kennis hebben gemaakt met Hill-functies (zie ook Tip 1), gaan we terug naar het Lotka-Volterra model. Omdat het Lotka-Volterra model is uitgebreid met deze verzadigingsterm, moeten we opnieuw de nullclines uitrekenen en schetsen (ook die zijn veranderd!). Maar zoals je je wellicht kan voorstellen worden de nullclines iets ingewikkelder door deze non-lineaire term in onze vergelijkingen. Naar mate we onze modellen meer en meer uitbreiden, wordt het natuurlijk steeds lastiger om alles met de hand te doen. Daarom gaan we in dit hoofdstuk de faseruimte en het vectorveld laten tekenen door grind.R, een Rscript dat deze analyses een fluitje van een cent maakt!
| Naam | Vergelijking | Grafiek |
|---|---|---|
| Type II | \[\frac{x}{x+h}\] |  |
| Type III | \[\frac{x^2}{x^2+h^2}\] | 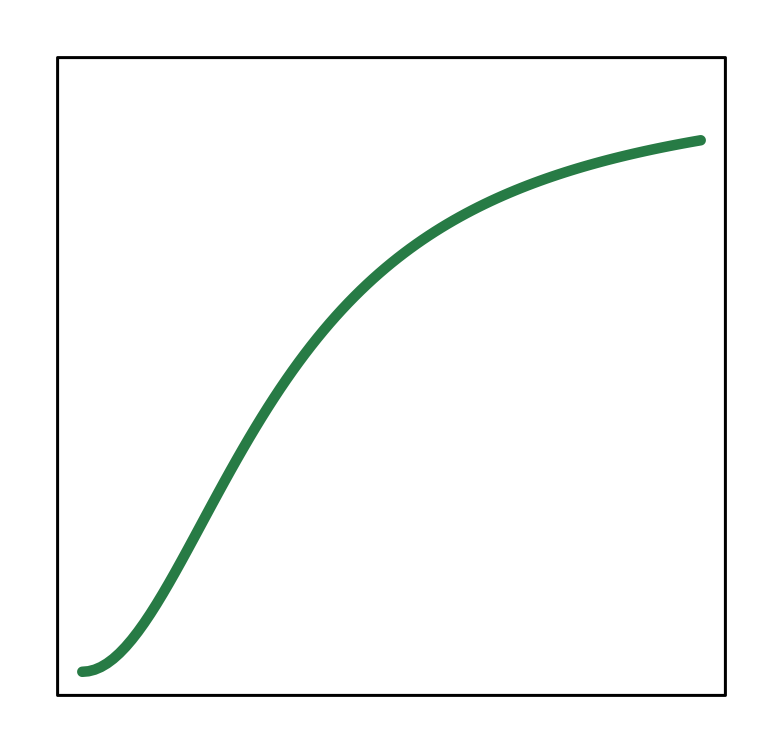 |
| Type II (afnemend) | \[1-\frac{x}{x+h} = \frac{1}{x/h+1}\] | 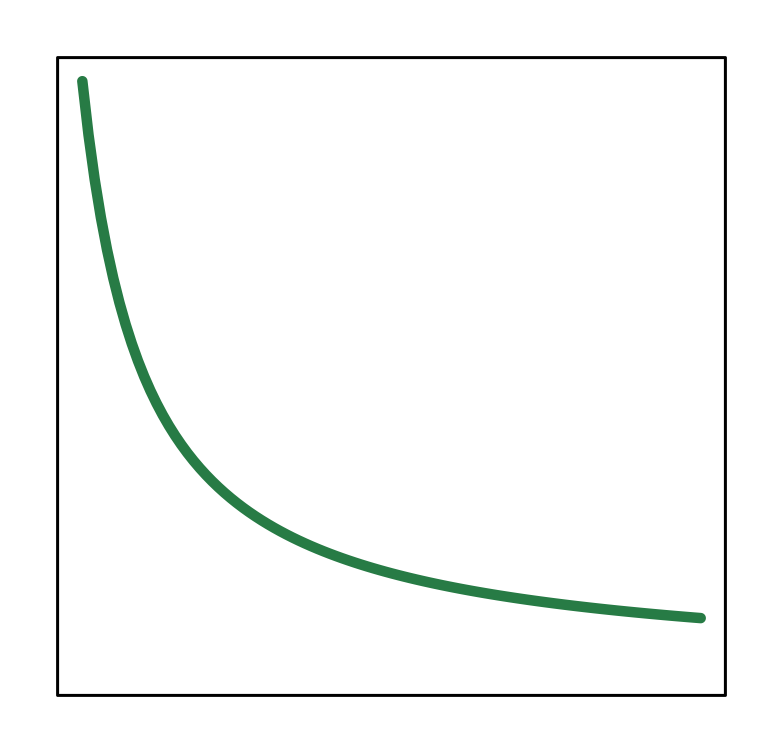 |
| Type III (afnemend) | \[1-\frac{x^2}{x^2+h^2} = \frac{1}{\frac{x^2}{h^2}+1}\] | 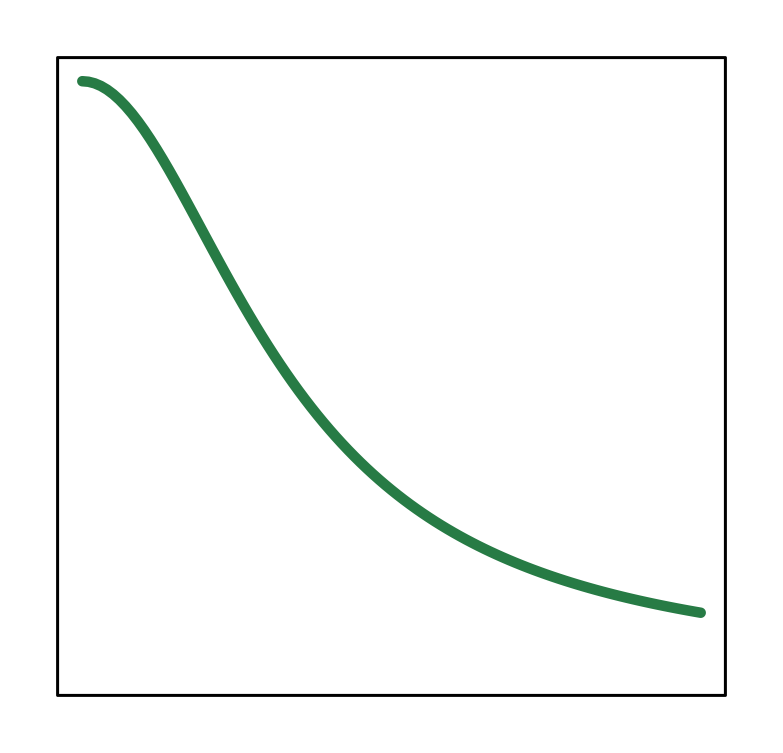 |
Grind tutorial
Grind (GReat INtegrator Differential equations) is een Rscript geschreven door Rob de Boer (https://tbb.bio.uu.nl/rdb), wat het heel makkelijk maakt om faseruimtes, vectorvelden, en oplossingen te berekenen en plotten. Ook kun je Grind gebruiken om modellen te fitten aan experimentele data, zodat je op basis van metingen in het veld parameters als \(b\), \(d\), \(K\), en \(h\) zou kunnen schatten. Dat laatste is heel relevant wanneer modellen gebruikt worden voor (bijvoorbeeld) belangrijke beleidsbeslissingen, maar in deze cursus gaan we het vooral gebruiken om gemakkelijk faseruimtes met nullclines te schetsen, en oplossingen te bestuderen. De volledige handleiding en introductie tot Grind vind je hier.
Voordat je Grind kan gebruiken, moet je eenmalig een paar “packages” in R installeren:
Nadat deze packages zijn geinstalleerd, moeten we het grind.R script inladen. Dit kan je vanaf de website doen:
source("https://tbb.bio.uu.nl/rdb/grindR/grind.R")Of vanaf je eigen computer als je het script hebt gedownload:
source("C:/Student/Modellen/grind.R")Als het laden van het script goed is gegaan, krijg je een melding:
grind.R (25-06-2024) was sourcedNu kunnen we grind.R gebruiken. De differentiaalvergelijkingen staan in een functie genaamd ‘model’1:
En vervolgens geef je de parameters en begin-waarden (initial condition) voor de variabelen aan:
p <- c(b=1,d=0.01,K=1,a=1,c=1,delta=0.3,c=1,h=1) #parameters
s <- c(R=1.1,N=0.25) #begin-dichtheden van R en N
colors[1] = "blue"
colors[2] = "#FF7F50"Hierboven geef ik ook even de nieuwe kleuren aan voor de ‘eerste’ en ‘tweede’ vergelijking, zodat dit overeenkomt met de kleuren die we tot nu toe hebben gebruikt. Dit is niet noodzakelijk, maar zo raken we niet in de war.
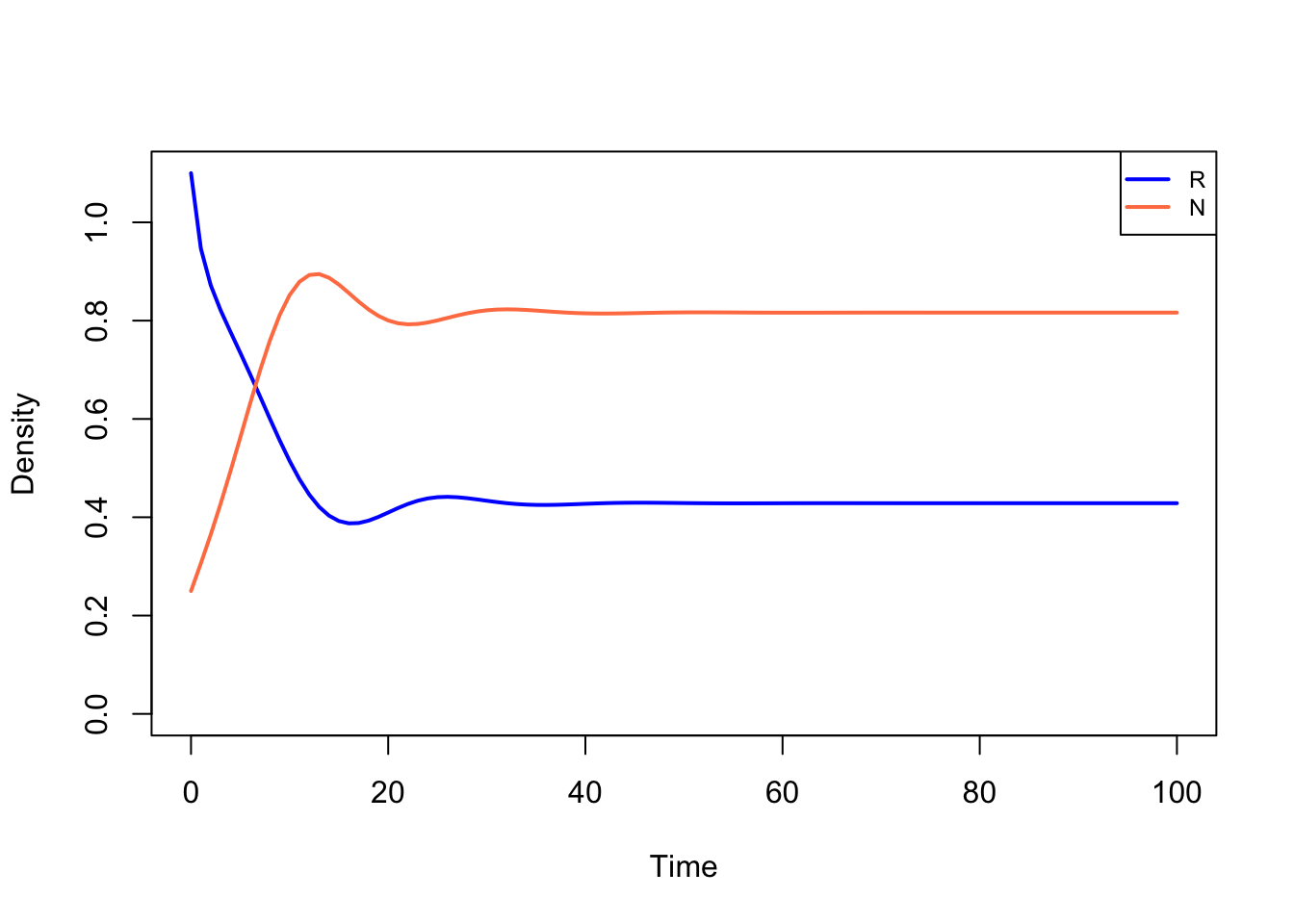
Nu kun je met met de functie run eenvoudig een oplossing uitrekenen:
Zoals je ziet genereert Grind een grafiek (een oplossing), en vertelt het ook meteen wat de eind-waarden zijn van je variabelen.
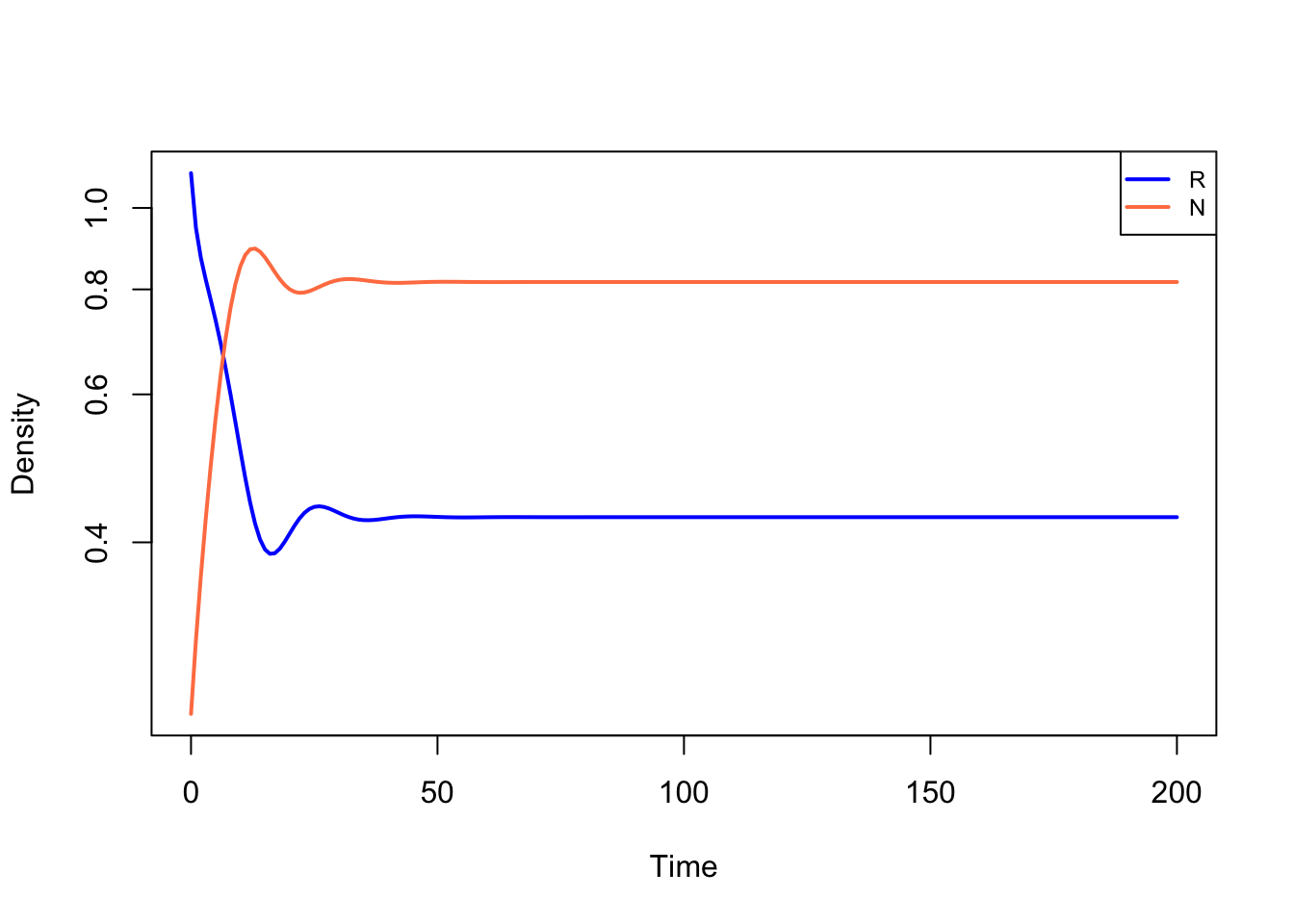
We kunnen ook argumenten aan run meegeven, bijvoorbeeld om wat langer door te rekenen (tmax, deze optie is standaard 100) en een optie om y-as logaritmisch te schalen:
Zoals je ziet zijn de waarden na tijdstip 100 niet meer veel veranderd. Het systeem was dus eigenlijk al (bijna) in evenwicht.
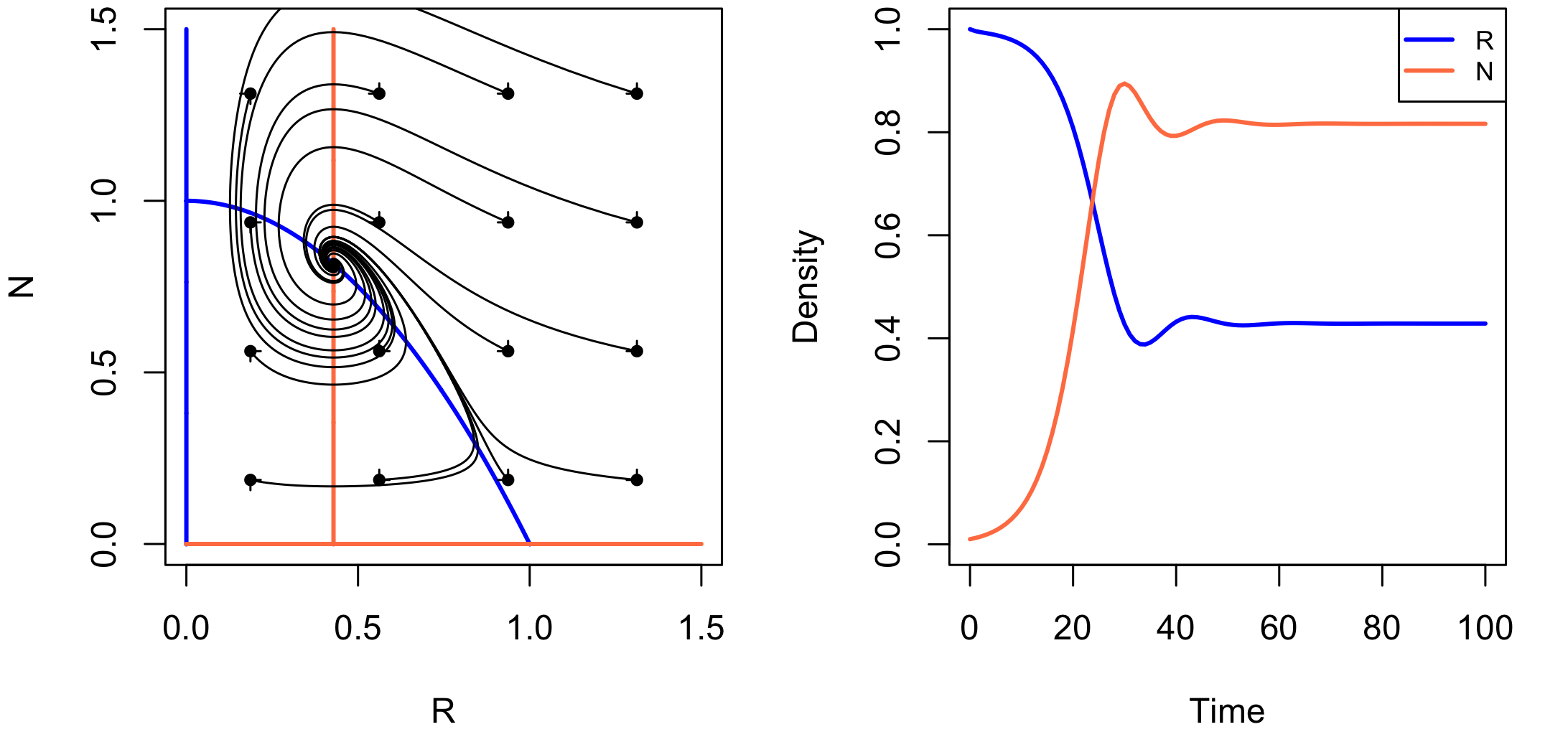
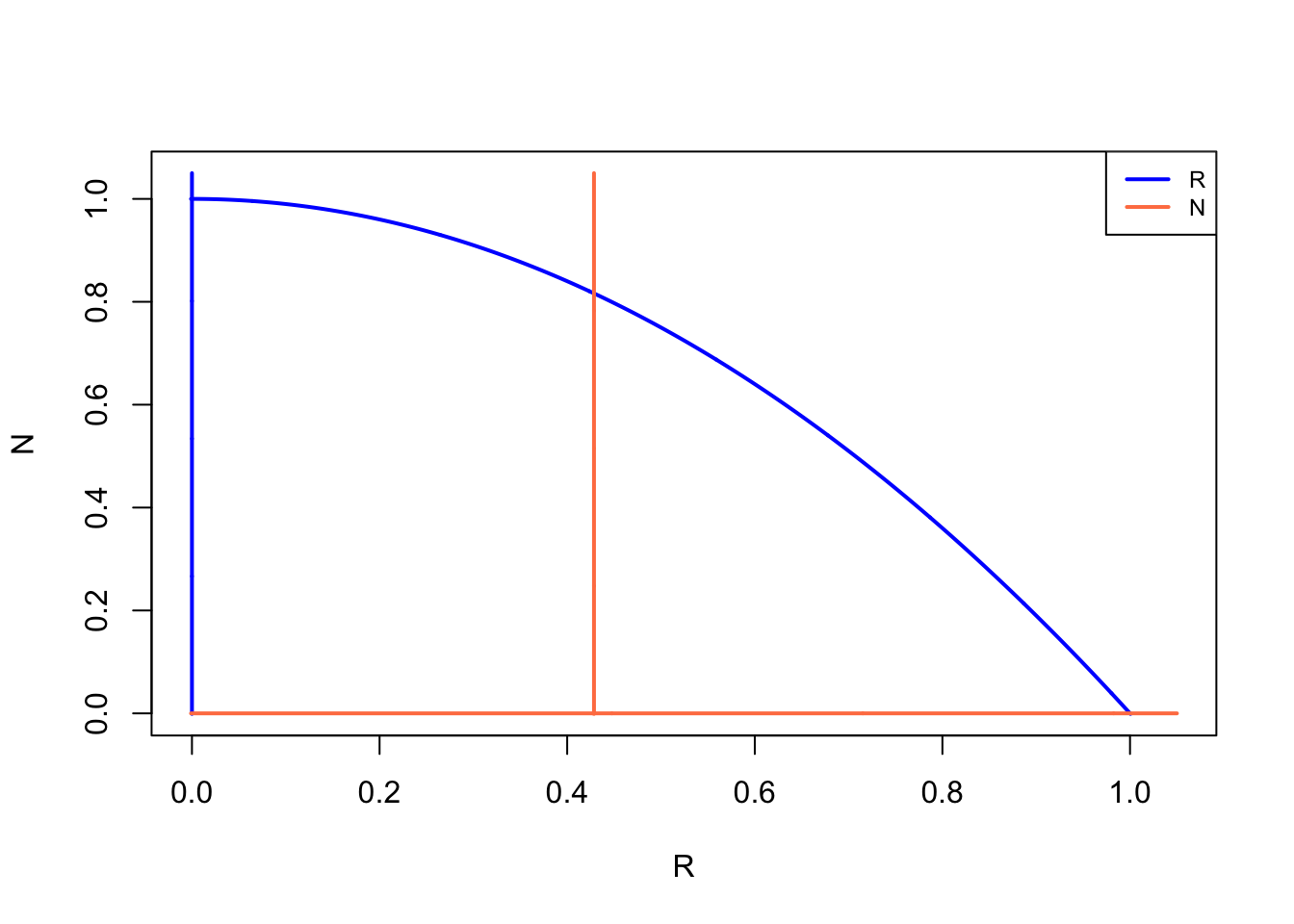
We kunnen ook een faseruimte maken met de functie plane:
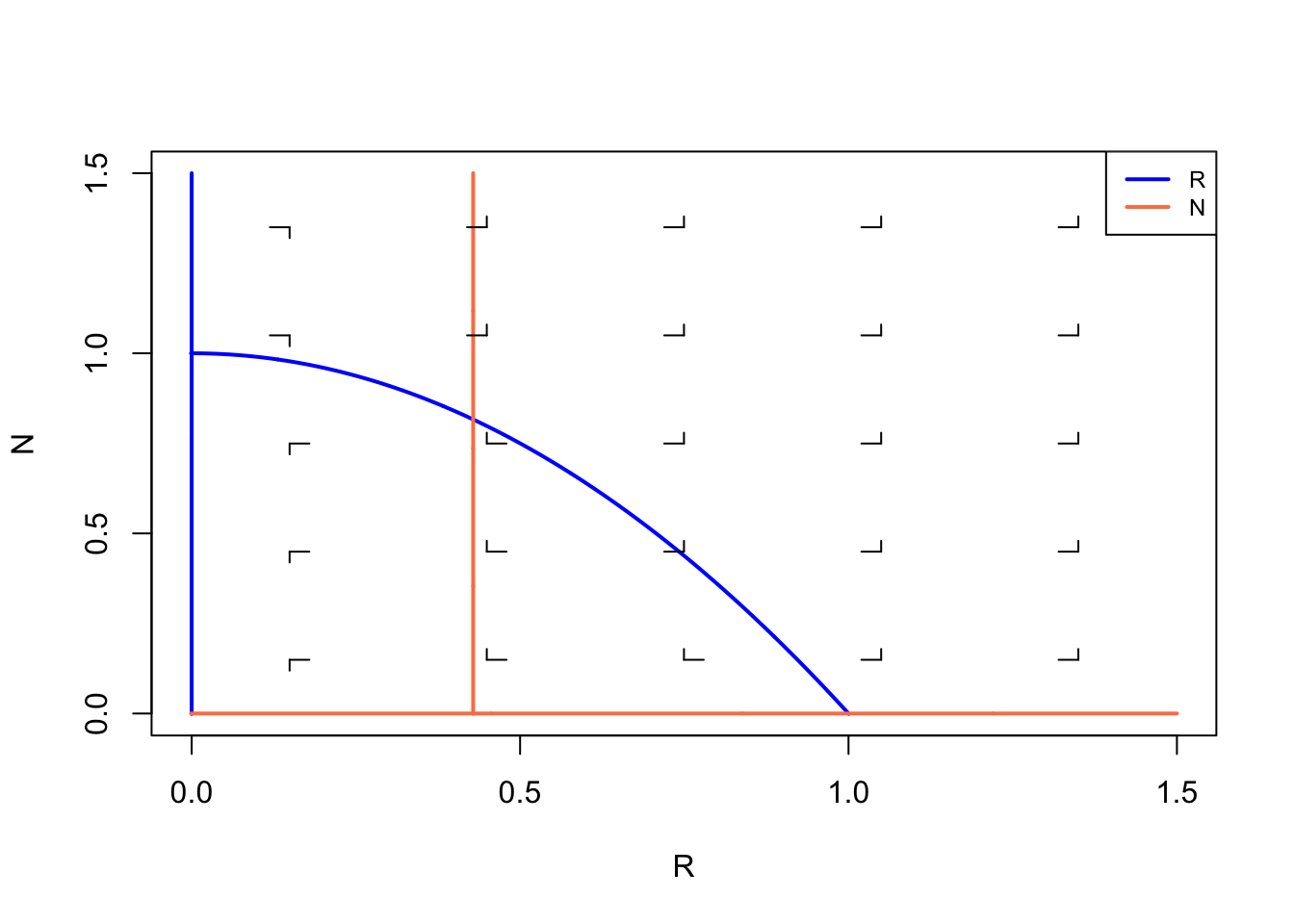
Ook deze functie kunnen we weer argumenten meegeven, bijvoorbeeld om de assen iets verder te vergroten en een vectorveld te tekenen:
Als laatste willen we (net als in het vorige hoofdstuk) weten of de evenwichten stabiel of instabiel zijn. Hiervoor geven we Grind een geschatte waarde dichtbij een evenwicht mee, en gebruiken we de functie newton:
plane(xmax=1.5, ymax=1.5,vector = T)
newton(state=c(R=0.0,N=0.0),plot=T)
newton(state=c(R=1.0,N=0.0),plot=T)
newton(state=c(R=0.4,N=0.8),plot=T)
run(traject = T,tstep=0.1)De laatste regel gebruikt run met de optie traject=T om een trajectorie door de faseruimte te tekenen. Dit vertaalt het grafiekje door de tijd die we eerder hebben uitgerekend, naar een mooie inwaardse spiraal. Er zijn nog veel meer opties in grind.R. Als je wil zien welke argumenten een functie allemaal kent, kun je gebruik maken van args:
args(plane)function (xmin = -0.001, xmax = 1.05, ymin = -0.001, ymax = 1.05,
xlab = "", ylab = "", log = "", npixels = 500, state = s,
parms = p, odes = model, x = 1, y = 2, time = 0, grid = 5,
eps = NULL, show = NULL, addone = FALSE, portrait = FALSE,
vector = FALSE, add = FALSE, legend = TRUE, zero = TRUE,
lwd = 2, col = "black", pch = 20, ...)
NULLZo zie je bijvoorbeeld dat je de legenda zou kunnen verbergen met de legend optie, of de lijndikte (lwd) zou kunnen aanpassen. Met andere woorden: met R kunnen we zonder al te veel rekenwerk prachtige figuren genereren en wiskundige modellen doorrekenen!
Lotka-Volterra in Grind
Als je de bovenstaande tutorial hebt gevolgd (en de packages hebt geïnstalleerd), kun je nu het volgende script overnemen en aan de slag met het uitbreiding van het Lotka-Volterra model waar de predatieterm verzadigt:
model <- function(t, state, parms) {
with(as.list(c(state,parms)), {
dR <- b*R*(1 - R/K) - d*R - a*R*N/(R+h)
dN <- c*a*R*N/(R+h) - delta*N
return(list(c(dR, dN)))
})
}
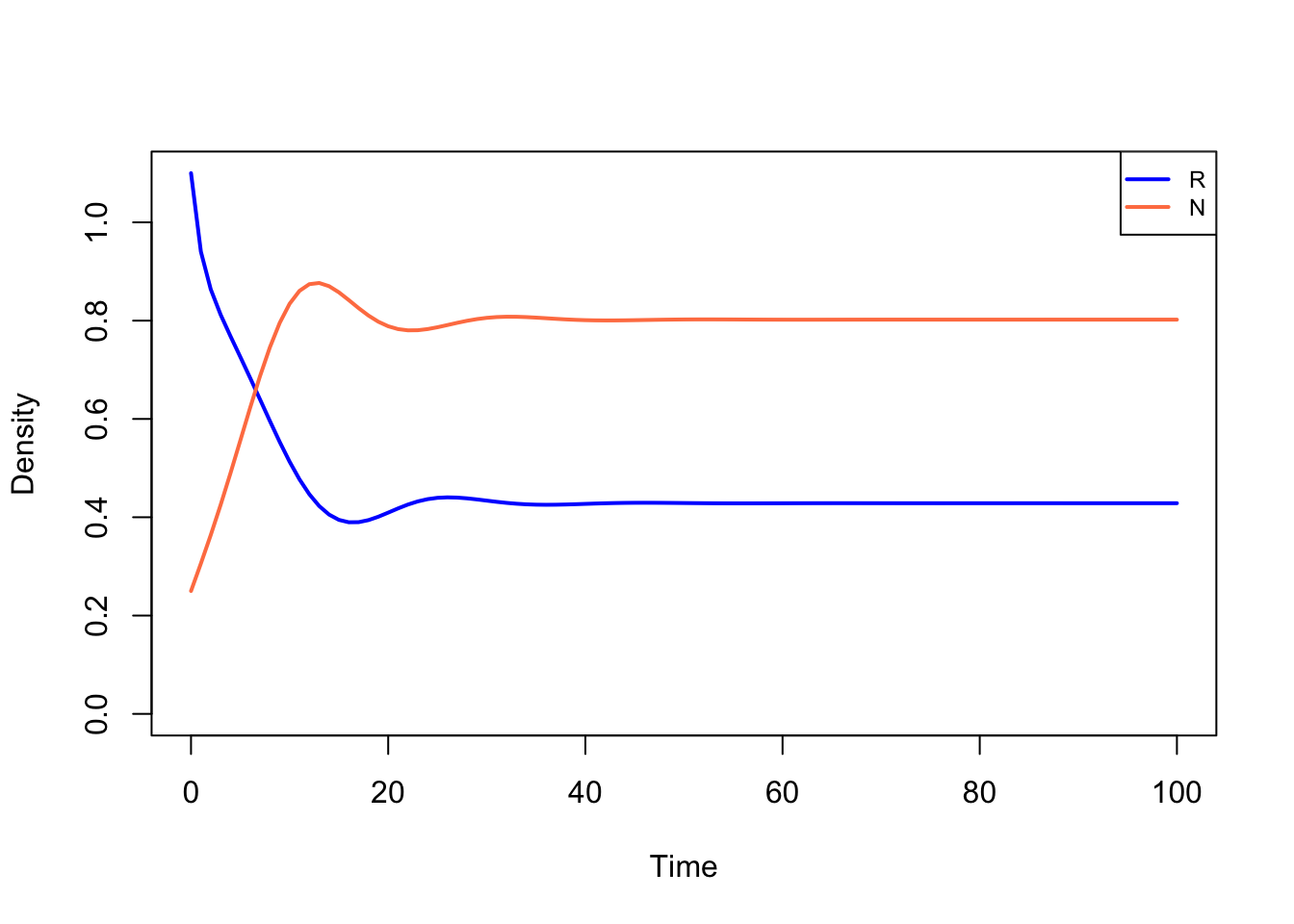
p <- c(b=1,d=0.1,K=2,a=1,c=1,delta=0.3,c=1,h=1) #parameters
s <- c(R=1.1,N=0.1) #begin-dichtheden van R en N
colors[1] = "blue" #optioneel, default = 'red'
colors[2] = "#FF7F50" #optioneel, default = 'blue'
par(mfrow=c(1,2)) # optioneel, maakt 2 plotjes naast elkaar
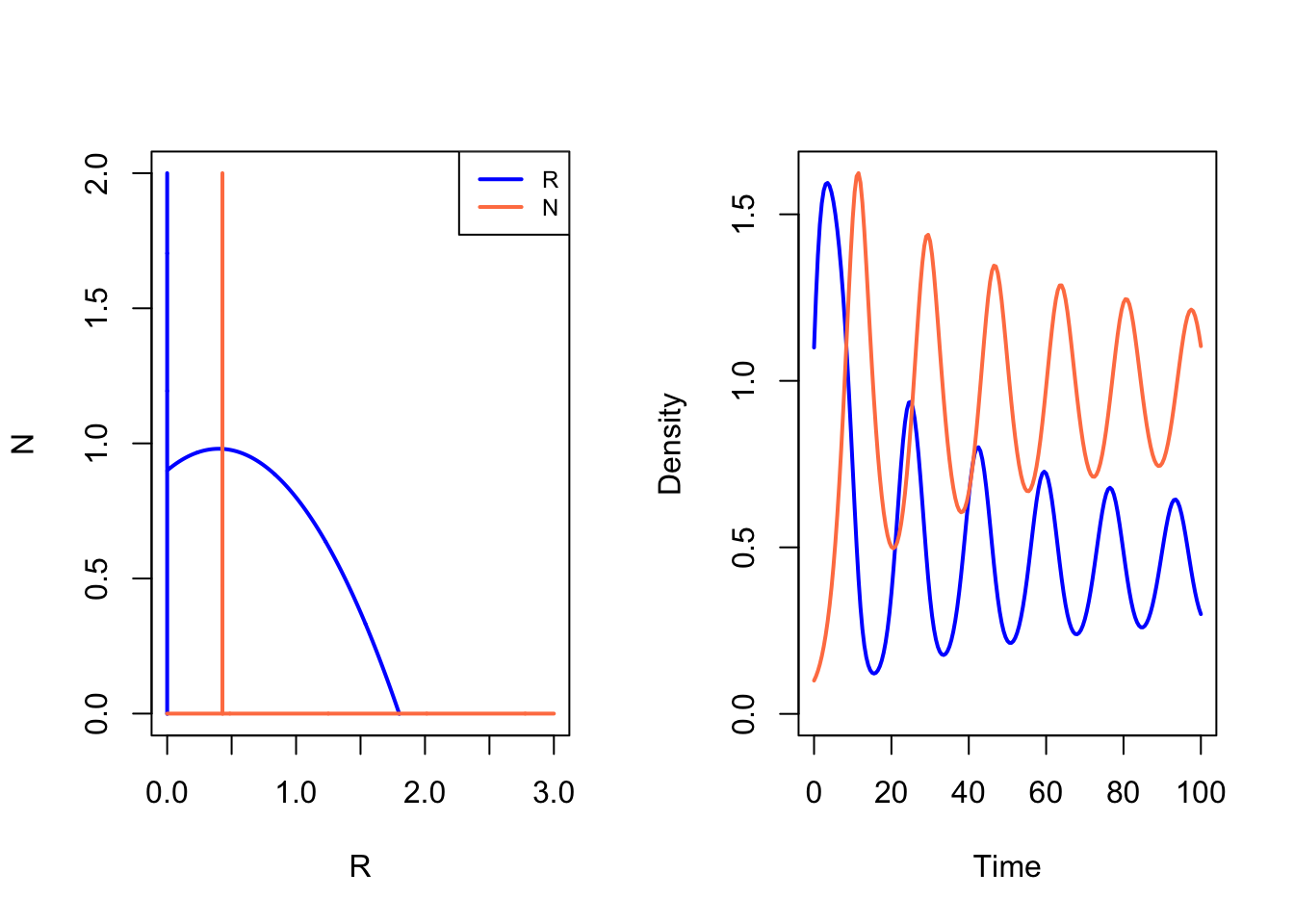
plane(xmax=3,ymax=2)
run(tstep=0.5, legend=F) R N
0.2995413 1.1041111 Door te oefenen met dit R-script, naast de pen en papier opgaven, is het de bedoeling dat je een goed gevoel ontwikkelt voor ODEs: wiskundige modellen die veel in de biologische literatuur voorkomen. Hieronder volgt een korte vraag, om met zowel pen en papier als Grind te oefenen.
Oefening 1 (De nieuwe nullcline voor de prooi)
Hierboven hebben we nullclines gegenereerd van het vernieuwde Lotka-Volterra model (met een verzadigbare predator). Zoals je ziet is dit geen rechte lijn meer.
- Bepaal met pen en papier aan welke functie de vernieuwde nullcline voor de prooi voldoet.
- Wat is het effect van de \(K\) parameter op de ligging van deze nullcline?
- Neem het R-script hierboven over met het Lotka-Volterra model met verzadigbare predator. Verdubbel de waarde van \(K\). Wat valt je op?
Bifurcaties van evenwichten
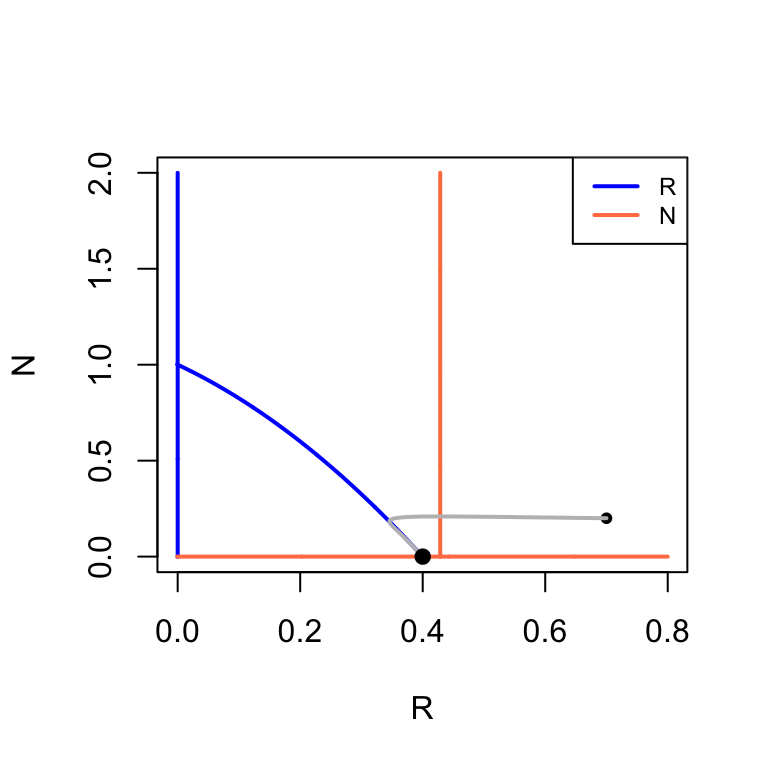
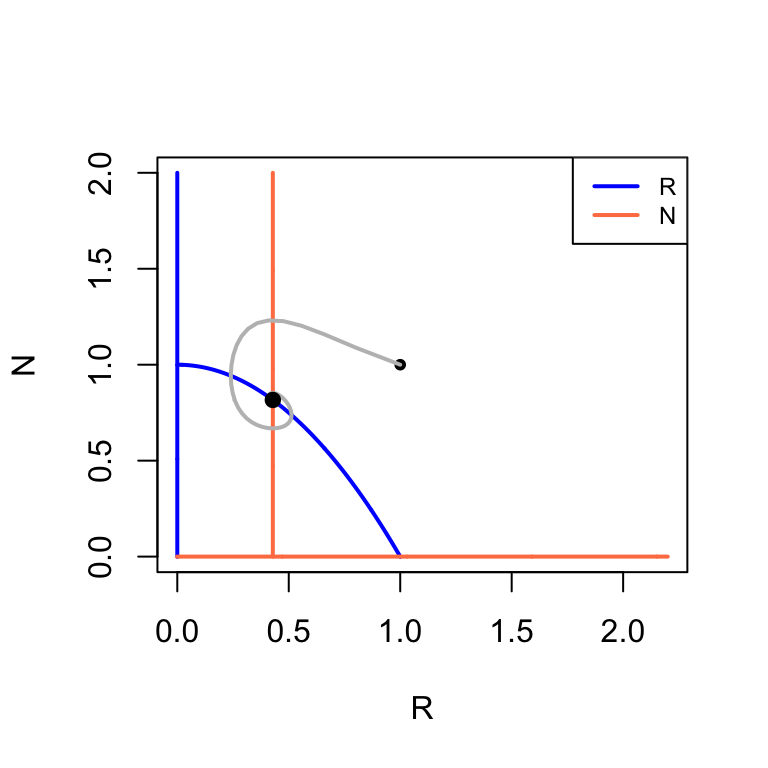
Het model met verzadigbare predator heeft een interessante eigenschap: afhankelijk van de parameters kan het type evenwicht veranderen. Iets dergelijks zagen we ook al eerder terug: de predator kon alleen samenleven met de prooi als de parameters dat toelieten. Deze transitie zien we ook terug in dit vernieuwde model (van Figuur 2 (a) naar Figuur 2 (b)). Deze bifurcatie (van geen samenleving naar wél samenleving) wordt een kritische transitie genoemd. Echter is er met dit vernieuwde model een tweede bifurcatie mogelijk: de predator-nullcline kan de prooi-nullcline links of rechts van de top van de parabool snijden (van Figuur 2 (b) naar Figuur 2 (c)). Als het snijpunt links van de top van de parabool ligt, zien we voortdurende oscillaties van predator en prooi, waarbij de populaties om het instabiele evenwicht heen blijven draaien. Eerder hadden we al gezegd dat attractoren niet altijd hetzelfde zijn als het evenwichtspunt, en hier zie je dat heel goed! Deze attractor, waarbij de populaties constant om het evenwicht heen blijven draaien, heet een limietcyclus. De overgang van de stabiele spiraal (snijpunt rechts van de parabool) naar de instabiele2 spiraal (snijpunt links van de parabool) staat bekend als de Hopf-bifurcatie.
Code
model <- function(t, state, parms) {
with(as.list(c(state,parms)), {
dR <- b*R*(1 - R/K) - d*R - a*R*N/(R+h)
dN <- c*a*R*N/(R+h) - delta*N
return(list(c(dR, dN)))
})
}
colors[1] = "blue" #optioneel, default = 'red'
colors[2] = "#FF7F50" #optioneel, default = 'blue'
p <- c(b=1,d=0.0,K=0.4,a=1,c=1,delta=0.3,c=1,h=1) #parameters
s <- c(R=0.7,N=0.2) #begin-dichtheden van R en N
plane(xmax=0.8,ymax=2)
run(tstep=0.5, traject=T,col="grey")
newton(state=c(R=0.4,N=0.0),plot=T)
p <- c(b=1,d=0.0,K=1,a=1,c=1,delta=0.3,c=1,h=1) #parameters
s <- c(R=1,N=1) #begin-dichtheden van R en N
plane(xmax=2.2,ymax=2)
run(tstep=0.5, traject=T,col="grey")
newton(state=c(R=0.5,N=0.5),plot=T)
p <- c(b=1,d=0.0,K=2,a=1,c=1,delta=0.3,c=1,h=1) #parameters
s <- c(R=1.2,N=1.3) #begin-dichtheden van R en N
plane(xmax=2.2,ymax=2)
run(tstep=0.2, traject=T,col="grey")
newton(state=c(R=0.5,N=0.5),plot=T)
newton(state=c(R=0.0,N=0.0),plot=T)
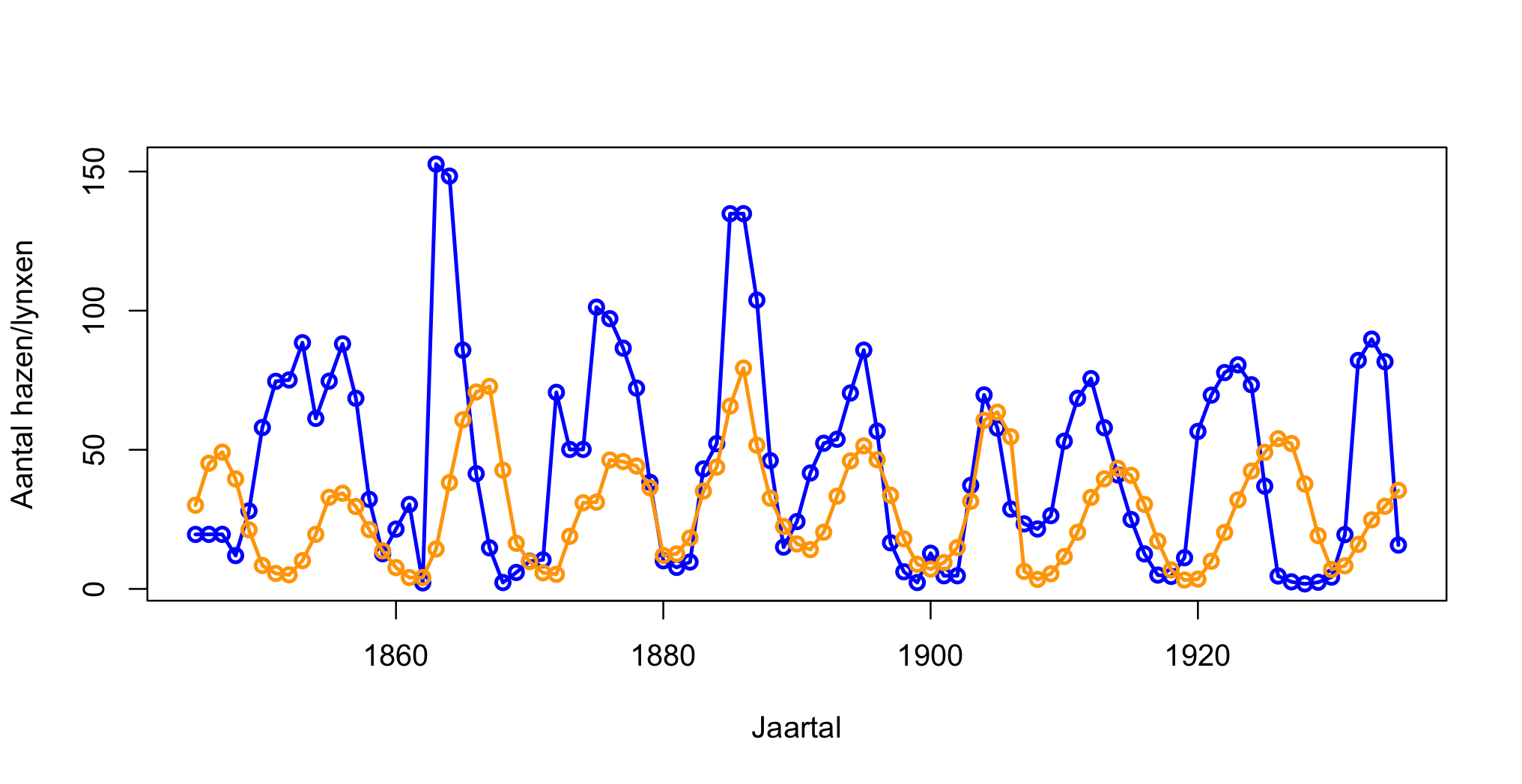
newton(state=c(R=2.0,N=0.0),plot=T)Voortdurende oscillaties tussen prooi en predator worden inderdaad waargenomen, bijvoorbeeld de oscillaties tussen hazen en lynxen in Noord Amerika (Figuur 3). Ook in experimenten zijn dergelijke oscillaties waargenomen, bijvoorbeeld door Paramecium (een-cellige protist, prooi) en Didinium (eencellige protist, predator) samen te groeien in een Erlenmeyer (Xia et al., 1992).
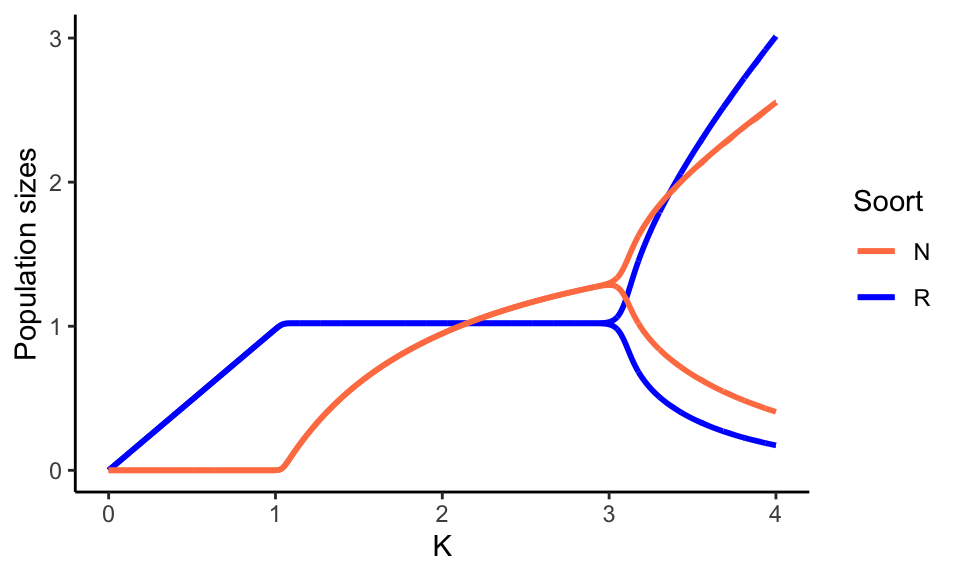
Bifurcaties kun je weergeven in een bifurcatiediagram, waarbij we de parameter die het evenwicht beïnvloedt op de x-as zetten, en de populatiegroottes in evenwicht op de y-as. Als we dit doen voor de bovenstaande bifurcaties, krijgen we dit:
Code
my_theme <- theme_bw() +
theme(panel.border = element_blank(), panel.grid.major = element_blank(),
panel.grid.minor = element_blank(), axis.line = element_line(colour = "black"))
model <- function(t, state, parms){
with(as.list(c(state,parms)),{
dR <- R*(b*(1-R/K)-d) - a*R*N/(R+h)
dN <- c*a*R*N/(R+h) - delta*N
return(list(c(dR,dN)))
})
}
# all <- data.frame()
# for(k in c(0.00001,seq(0.001,4.0,by=0.001))){
# p <- c(a=0.5,delta=0.25,b=0.5,d=0.01,c=0.99,K=k,h=1)
# s <- c(R=0.4,N=0.4)
# plane(ymax=1.2,ymin=-0.1,xmin=-0.01, xmax=1.2,tstep=0.01,tmax=50)
# #res <- newton()
# dat <- run(table=T,step=11,tmax=1000,timeplot=F)
# dat$K = k
# all <- rbind(all,tail(dat,100))
# cat(k,"\n")
# }
#
# bifurcation_data <- all %>% group_by(K) %>%
# mutate(maxN=max(N)) %>%
# mutate(minN=min(N)) %>%
# mutate(maxR=max(R)) %>%
# mutate(minR=min(R)) %>%
# filter(time==1000) %>%
# distinct()
#
# write.table(bifurcation_data, "Modellering/figuren/bifurcation_data.csv")
bifurcation_data <- read.table("figuren/bifurcation_data.csv")
#list.files("figuren")
colors <- c("R" = "blue", "N" = "#FF7F50")
bifurcation_data %>%
ggplot(aes(x=K,y=maxN)) +
#geom_line(col="#FF7F50",linewidth=1, aes(color="N")) +
geom_line(aes(y=maxR,color="R"),linewidth=1) +
geom_line(aes(y=minR,color="R"),linewidth=1) +
geom_line(aes(y=minN,color="N"),linewidth=1) +
geom_line(aes(y=maxN,color="N"),linewidth=1) +
ylab("Population sizes") +
my_theme +
scale_color_manual(name="Soort",values = colors)Omdat er bij hoge waarden van \(K\) oscillaties zijn, geven de lijnen de minimale en maximale waarde van deze oscillaties aan. Omdat de parameter \(K\) het draagvlak van de prooi beinvloed, geeft dit diagram dus weer wat er bijvoorbeeld zou gebeuren als we konijnen op de Veluwe gaan bijvoeren: eerst krijgen we meer konijnen, dan krijgen we alleen meer predatoren, en daarna begint het systeem harder en harder te schommelen! Zo zie je: het behoud van biodiversiteit is zelfs in dit simplistische “ecosysteem” niet triviaal!
grind.R kan nog veel meer
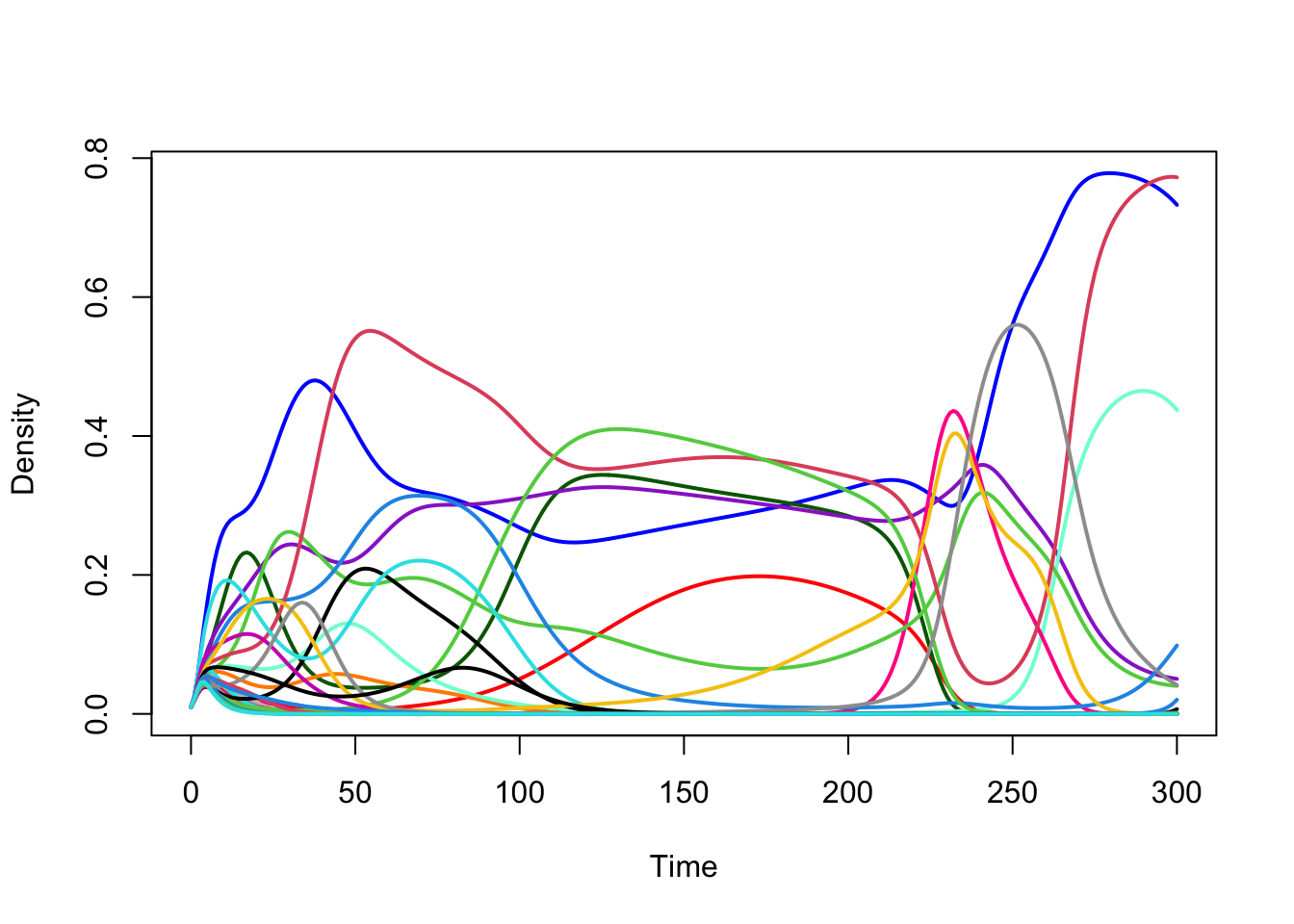
Met het R-script grind.R kan je nog veel meer dan alleen faseplaatjes en bifurcaties analyseren. Zo kan je bijvoorbeeld met een zogeheten “interactie matrix” (waarin staat hoe alle soorten interacteren met alle soorten) een heel ecosysteem doorrekenen (zie Figuur 5 voor een voorbeeld met 30 soorten), wat fascinerend complexe en onvoorspelbare dynamiek kan opleveren. Hoewel het brede scale aan functionaliteiten van grind.R leuk zijn om mee te spelen, is dit geen leerstof. De algemene boodschap is dat we voor meer ingewikkelde systemen meestal niet met pen en papier te hoeven rekenen, maar de computer het werk kunnen laten doen!
Code
source("https://tbb.bio.uu.nl/rdb/grindR/grind.R")
set.seed(12)
model <- function(t, state, parms) {
N <- state
S <- A %*% N # R code for matrix x vector multiplication
dN <- r*N*(1 - S)
return(list(dN))
}
p <- c()
n <- 30
s <- rep(0.01,n)
names(s) <- paste("N",seq(1,n),sep="")
r <- abs(rnorm(n,1,0.1))
A <- matrix(runif(n*n),nrow=n,ncol=n)
diag(A) <- 1; A
run(tmax=300,legend=F)Terminologie
| Nederlands | Engels | Beschrijving |
|---|---|---|
| Hill-functies | Hill functions | Een set wiskundige functies die verzadigen bij grote waarden (ze hebben een horizontale asymptoot). |
| Kritische-transitie | Critical Transition | Een punt waarbij een parameter-verandering het gedrag van een model fundamenteel verandert, bijvoorbeeld doordat het aantal of de stabiliteit van de evenwichten verandert. In dit hoofdstuk zien we bijvoorbeeld dat er alleen samenleving mogelijk is als \(K\) hoog genoeg is. Er is dus een waarde van \(K\) waarbij er een kritische transitie is. |
| Hopf-bifurcatie | Hopf-bifurcation | Een omslagpunt waar, als je een bepaalde parameter verandert, een stabiel evenwicht overgaat in periodiek gedrag (of andersom). In dit hoofdstuk zagen we dit terug doordat het verhogen van \(K\) de stabiele samenleving van predator en prooi kan veranderen in periodieke oscillaties van de populatiegroottes. |
Op regel 2 zie dat dat deze ‘model’-functie zit een beetje raar zit ingepakt in een
withfunctie. Dit heeft een technische reden (en is zeker geen leerstof), maar helpt R begrijpen hoe de variabelen/parameters heten. De enige regels die je eigenlijk hoeft aan te passen zijn degene met de vergelijkingen (hier regel 3 en 4), en zorgen dat deze vergelijkingen in de goede volgorde worden teruggegeven (regel 5).↩︎Het kan zijn dat je nog niet weet wat stabiele en instabiele spiralen zijn, daar leren we in een later hoofdstuk over↩︎