22  Kansen en kansmodellen

In de eerdere hoofdstukken hebben we benadrukt dat bijna alle biologische gegevens onzeker zijn, door meetfouten en steekproevenvariabiliteit. Om te begrijpen wat we wel of niet kunnen concluderen uit zulke onzekere gegevens, berekenen we kansen (probabilities). In dit hoofdstuk geven we daarom een korte introductie in kansrekenen.

22.1 Leerdoelen

Na het bestuderen van dit hoofdstuk kun je:

• de basisbegrippen van kansrekenen, zoals kansexperiment, kansvariabele, kansruimte, en gebeurtenis, uitleggen en toepassen;
• uitleggen dat voor het toepassen van kansrekenen altijd een kansmodel nodig is;
• gebeurtenissen weergeven in een Venn-diagram;
• uitleggen wat conditionele kansen zijn;
• bepalen of twee gebeurtenissen onafhankelijk zijn, en of ze elkaar uitsluiten;
• de rekenregels voor kansen toepassen voor het berekenen van samengestelde kansen;
• de Stelling van Bayes toepassen.

22.2 Basisbegrippen

Wanneer je een dobbelsteen gooit, weet je van vooraf niet welk getal boven komt te liggen. Zo’n experiment, gebeurtenis of proces met een onzekere uitkomst wordt een kansexperiment (random experiment) genoemd. Andere voorbeelden zijn het willekeurig trekken van een eenheid uit een populatie, een draai aan het roulette-wiel, of het aantal mutaties in een genoom na blootstelling aan UV-licht.

Een kansvariabele (random variable) is een variabele waarvan de waarde een functie is van de uitkomst van een kansexperiment. Een voorbeeld is het aantal ogen van een dobbelsteen, of het kwadraat van het aantal ogen van een dobbelsteen. Andere woorden voor kansvariabele zijn stochastische variabele (stochastic variable) of stochast. Een kansvariabele wordt meestal aangeduid met een hoofdletter, zoals \(X\) of \(Y\).

Eerder hebben we verschillende typen variabelen besproken, zoals continu, discreet, nominaal en ordinaal (zie Figuur 20.1). Kansvariabelen kunnen op dezelfde manier worden ingedeeld.

De verzameling van alle mogelijke uitkomsten van een kansexperiment wordt de kansruimte (sample space) genoemd. Bij een normale dobbelsteen is de kansruimte de verzameling \[ \left\{ 1, 2, 3, 4, 5, 6 \right\}. \]

Soms zijn we geïnteresseerd in de kans op een specifieke uitkomst. De kans dat de uitkomst gelijk is aan 2 noteren we als \(\textrm{Pr}\!\left[X = 2\right]\). (De letters Pr staan hier voor Probability.)

In andere gevallen willen we weten wat de kans is op een bepaalde gebeurtenis (event). Bijvoorbeeld, laat \(X\) het aantal ogen zijn bij een worp met een dobbelsteen. Dan kunnen we vragen naar de kans dat \(X\) een oneven getal is: \[ \textrm{Pr}\!\left[X \textrm{ is oneven}\right]. \] Merk op: de gebeurtenis “\(X\) is oneven” is niet één specifieke uitkomst, omdat meerdere mogelijke uitkomsten oneven zijn (namelijk 1, 3, en 5). We kunnen dezelfde gebeurtenis ook zo schrijven: “\(X\) is een element van de verzameling \(\left\{1, 3, 5\right\}\).” Iedere gebeurtenis kan dus worden geïdentificeerd met een deelverzameling van de kansruimte.

Oefening 22.1 (Basisbegrippen van kansrekenen)

Identificeer van de volgende situaties het kansexperiment, de kansvariabele, de kansruimte, en de gebeurtenis waarin we geïnteresseerd zijn.

1. We kruisen twee heterozygote dieren (genotype aA) en onderzoeken de kans dat een nakomeling homozygoot recessief (aa) is.

2. We tellen het aantal teken aangetroffen op reeën in een bepaald bosgebied en vragen ons af hoe vaak we er minstens één aantreffen.

3. We willen weten hoe vaak na vaccinatie trombose met trombocytopenie-syndroom (TTS) optreedt. Daarom houden we van alle gevaccineerde personen bij of TTS is opgetreden.

4. Om de omvang te schatten van de brasem-populatie in het IJsselmeer en Markermeer willen we 2000 brasems vangen, merken, en weer teruggooien. Twee maanden later willen we er weer 2000 vangen en tellen hoeveel van deze vissen gemarkeerd zijn. We vragen ons af wat de kans is dat we geen enkele gemarkeerde brasem terugvangen als de populatiegrootte \(1{,}5\cdot 10^5\) is.

22.3 Kansen als frequenties van een lange serie identieke kansexperimenten

Wat is een kans nu eigenlijk precies?

Je kunt kansen op verschillende manieren definiëren, en over de beste interpretatie wordt al zeker een eeuw gedebatteerd. (Lees dit artikel als je daar meer over wilt weten.) Voor de meeste berekeningen maken de definitieverschillen niet uit.

In de statistiek wordt traditioneel vooral de frequentistische interpretatie van kansen gebruikt. In die interpretatie is de kans op een gebeurtenis gedefinieerd als de relatieve frequentie waarmee die gebeurtenis voorkomt in een héél lange reeks identieke kansexperimenten. Stel dat je steeds weer op dezelfde manier dezelfde eerlijke dobbelsteen gooit. Dan verwacht je dat, op de lange duur, een zesde van de uitkomsten 6 zal zijn. De relatieve frequentie van de uitkomst 6 in een héél lange reeks identieke kansexperimenten is dus \(\frac{1}{6}\). Daarom is de kans \(\textrm{Pr}\!\left[X = 6\right]\) gelijk aan \(\frac{1}{6}\).

De definitie heeft het over een héél lange reeks kansexperimenten. Hoe lang dan precies? Zolang het aantal keer dat je met de dobbelsteen gooit eindig is, kan de daadwerkelijke frequentie van zessen afwijken van \(\frac{1}{6}\). De frequentistische definitie van kansen gaat dus uit van een reeks kansexperimenten die tot in het oneindige wordt herhaald; alleen dan zal de frequentie van zessen met zekerheid convergeren naar \(\frac{1}{6}\).

Oefening 22.2 (De relatieve frequentie van 6 bij het gooien van een dobbelsteen)

In de tekst hierboven hebben we het over heel-erg-vaak gooien met een dobbelsteen. In de praktijk is dat lastig om te doen. Maar we kunnen dat natuurlijk wel simuleren!

Deze code in R gooit virtueel een miljoen keer een eerlijke dobbelsteen:

aantal_keer_gooien <- 10^6

resultaten <- sample(
  seq(1:6), # kies uit 1 tot 6
  size = aantal_keer_gooien, 
  replace = TRUE
  )

Het argument replace = TRUE zorgt ervoor dat we trekken “met terugleggen”, waardoor we meerdere keren hetzelfde getal kunnen trekken.

1. Maak in R een frequentietabel van de resultaten. Je hebt in Paragraaf 20.14.3 geleerd hoe dat moet; het is één regeltje code. Bereken ook de relatieve frequenties.

2. Bekijk hoe vaak je een 6 hebt gegooid. Komt dat exact overeen met een kans van \(\frac{1}{6}\)?

3. Wat is de kans dat de relatieve frequentie van de uitkomst “6” na een miljoen herhalingen exact gelijk is aan \(\frac{1}{6}\)?

Een relatieve frequentie ligt altijd tussen 0 en 1. Een kans is dus ook altijd een getal tussen 0 en 1 (inclusief 0 en 1). Als een gebeurtenis altijd plaatsvindt als we het kansexperiment uitvoeren, dan is de kans op die gebeurtenis 1. Als een gebeurtenis nooit gebeurt, hoe vaak we het kansexperiment ook herhalen, dan is de kans 0.

Soms worden kansen in percentages uitgedrukt, zoals “de kans op kop is 50%”. Daar is niets mis mee, maar formules met procenten worden al snel omslachtig. Wij houden het daarom bij getallen tussen 0 en 1.

Als de kansvariabele discreet is of categorisch, dan kunnen we de kansen van alle mogelijke uitkomsten optellen. Omdat de som van alle relatieve frequenties altijd gelijk is aan 1 moet de som van alle kansen ook altijd 1 zijn.

Warning 22.1: De som van alle kansen bij continue kansvariabelen

Bij discrete en categoriale kansvariabelen is de som van de kansen op de verschillende uitkomsten altijd gelijk aan 1: \[ \sum_x \textrm{Pr}\!\left[X = x\right] = 1 \] Hierbij loopt de sommatie over alle mogelijke waarden van \(x\), oftewel, de hele kansruimte.

Bij continue variabelen geldt ook zoiets, maar daar is alles wat ingewikkelder. Continue kansvariabelen hebben oneindig veel mogelijke uitkomsten, en bovendien is de kans op iedere mogelijke uitkomst meestal oneindig klein. Je kunt dus niet zomaar “alle kansen optellen”. Dat maakt dat je over continue kansvariabelen op een speciale manier moet nadenken. We komen daar later op terug.

22.4 Het toepassen van kansrekenen vereist altijd een model

Als je kansrekenen toepast in de werkelijke wereld moet je altijd aannames maken. Die aannames vormen samen een model van dat kansexperiment. Zo’n model wordt een kansmodel genoemd.

Bijvoorbeeld, stel dat je een dobbelsteen gooit en geïnteresseerd bent in de kans op een 6. Je hebt de dobbelsteen in een normale spelletjeswinkel gekocht, de dobbelsteen heeft een regelmatige kubusvorm, zijn oppervlak is overal glad, en zo te voelen is het gewicht evenredig verdeeld. Voor het gooien schud je de dobbelsteen goed.

Wat is dan een redelijk model?

Gezien de symmetrie van de dobbelsteen en de manier waarop je gooit is er geen reden om te verwachten dat de kansen op de mogelijke uitkomsten verschillen. Daarom neem je aan dat de kans op iedere uitkomst \(\frac{1}{6}\) is, en dus ook dat \(\textrm{Pr}\!\left[X = 6\right] =\frac{1}{6}\).

Het toepassen van kansrekenen is dus altijd een vorm van modelleren, zelfs in het simpele geval van een dobbelsteen. Dat de kans op een 6 gelijk is aan \(\frac{1}{6}\) is geen feit, maar volgt uit aannames die je maakt op basis van kennis over het kansexperiment. Als die aannames niet kloppen, geven je berekeningen geen betrouwbare voorspellingen.

22.5 Venn-diagrammen

Bij het denken over kansen helpt het soms om de kansruimte en de gebeurtenissen weer te geven in een Venn-diagram.

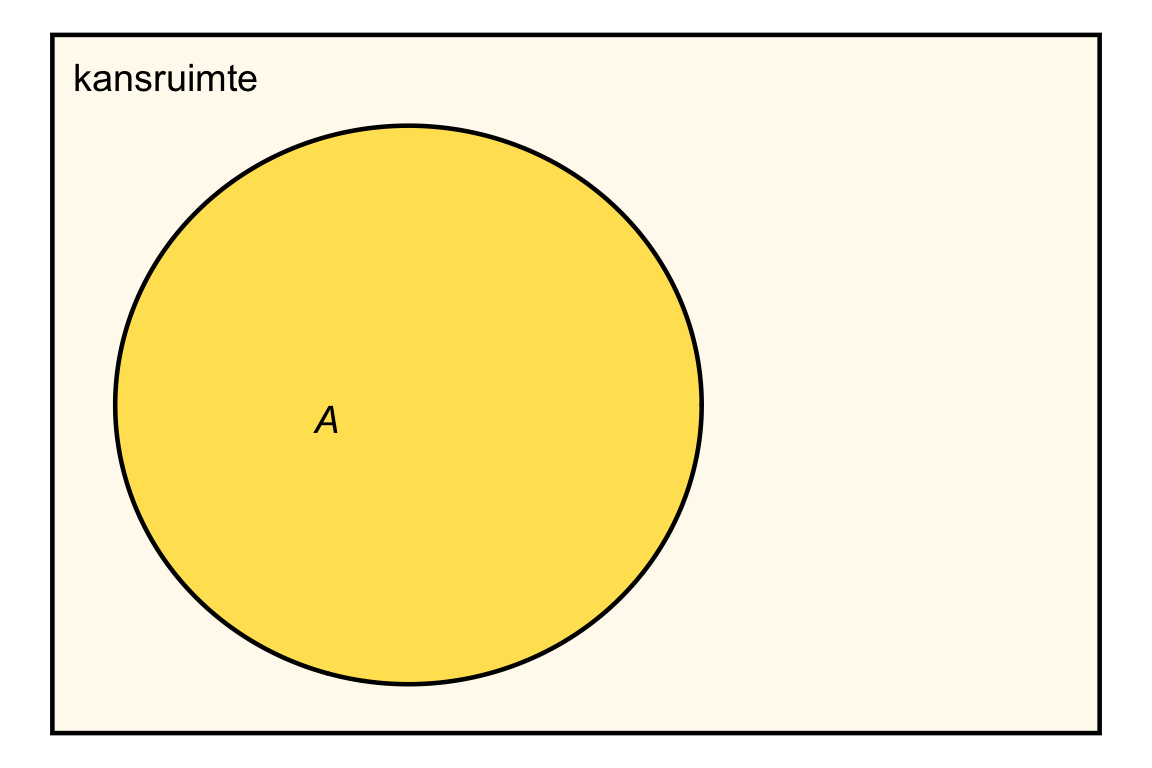
Je kunt je de verzameling van alle mogelijke uitkomsten (de kansruimte) voorstellen als een rechthoek (Figuur 22.1):

if (!("ggplot2" %in% .packages())){ 
  library(ggplot2) 
  }
if (!("ggforce" %in% .packages())){ 
  library(ggforce) 
  }

kleurKansruimte <- "FloralWhite"

kansruimte <- ggplot() +  
  geom_rect(
    aes(xmin = 0, ymin = 0, xmax= 100, ymax = 100),
    fill = kleurKansruimte, color = "black", linewidth = .8
    ) +
  annotate(
    "text", 
    x = 2, y = 94, 
    label = "kansruimte", 
    color = "black", 
    hjust = 0, 
    size = 5
    ) +
  theme_void()

kansruimte

Figuur 22.1: Een minimaal Venn-diagram. Het rechthoek stelt de volledige kansruimte voor.

Bijvoorbeeld, bij het gooien met één dobbelsteen staat de rechthoek voor de verzameling \(\{1, 2, 3, 4, 5, 6\}\).

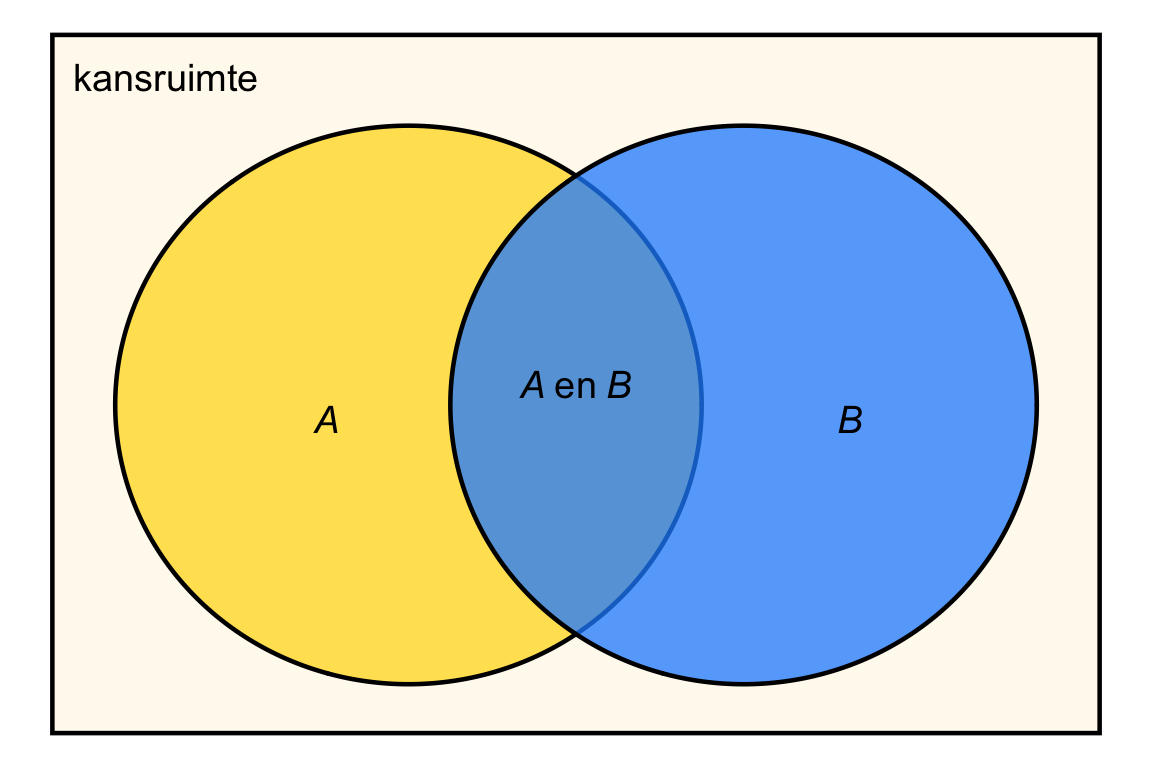
We zagen dat iedere gebeurtenis overeenkomt met een deelverzameling van de kansruimte. We kunnen een gebeurtenis \(A\) daarom voorstellen als een gedeelte van de kansruimte, hieronder in Figuur 22.2 weergegeven als een gele cirkel:

kleurA <- "Gold"

A <- list(
  geom_ellipse(
    aes(x0 = 34, y0 = 47, a = 28,  b = 40,  angle = 0), 
    fill = kleurA , alpha = 0.7, linewidth = .8
    ),
  annotate(
    "text", 
    x = 25, y = 45, 
    label = expression(italic(A)), 
    color = "black", 
    hjust = 0, 
    size = 5
    )
  )

kansruimte + A

Figuur 22.2: Venn-diagram met gebeurtenis \(A\). Een gebeurtenis is een deelverzameling van de kansruimte.

Binnen de cirkel liggen de uitkomsten waarbij gebeurtenis \(A\) plaatsvindt; buiten de cirkel de uitkomsten waarbij \(A\) niet plaatsvindt. Bijvoorbeeld, als \(A\) de gebeurtenis is dat we een even getal gooien, dan liggen de uitkomsten \(\{2, 4, 6\}\) binnen de cirkel, en de uitkomsten \(\{1, 3, 5\}\) erbuiten.

De kans op een uitkomst die binnen de rechthoek (kansruimte) valt, is 1. Het Venn-diagram laat zien dat de kans op \(A\) en de kans op niet \(A\) altijd optellen tot 1: \[\textrm{Pr}\!\left[A\right] + \textrm{Pr}\!\left[\text{niet } A\right] = 1.\] Daaruit volgt de complementregel: \[ \textrm{Pr}\!\left[A\right] = 1 - \textrm{Pr}\!\left[ \text{niet } A\right]. \qquad(22.1)\]

De gebeurtenis “\(A\) en \(B\)”

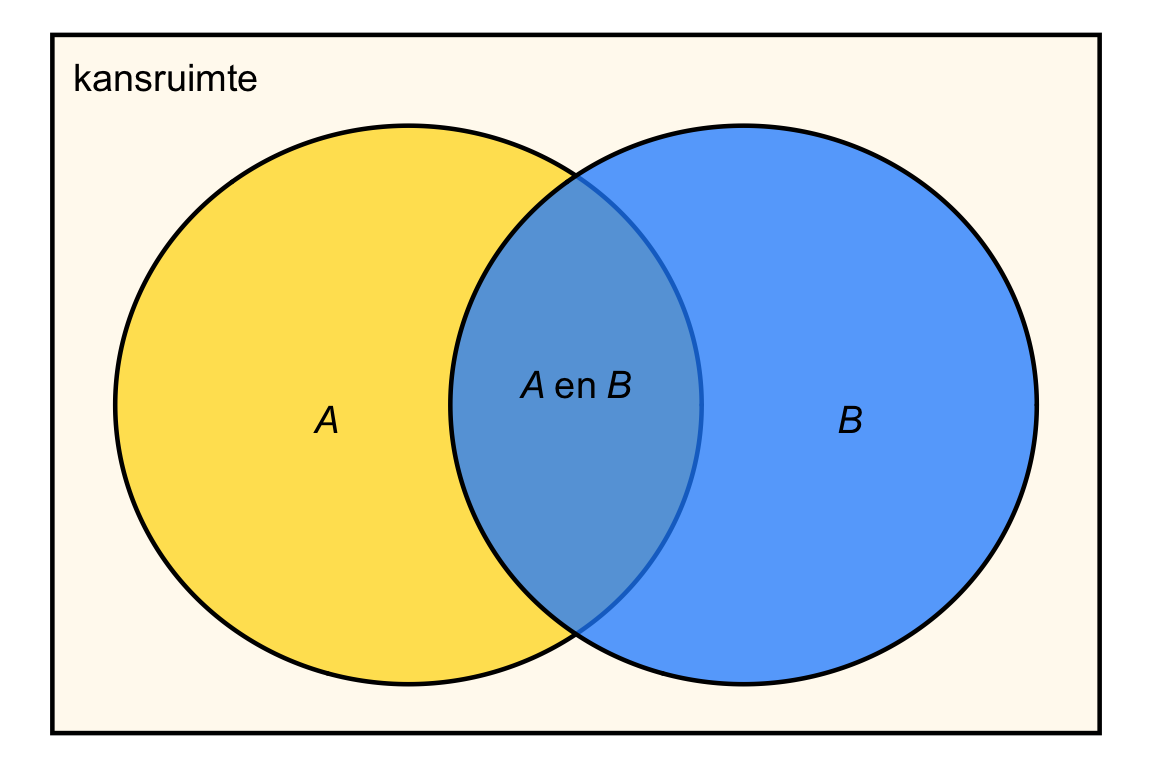
We kunnen ook meerdere gebeurtenissen in één diagram weergeven. Hieronder in Figuur 22.3 zie je bijvoorbeeld een Venn-diagram met gebeurtenissen \(A\) en \(B\):

kleurB <- "DodgerBlue"

B <- list( 
  geom_ellipse(
    aes(x0 = 66, y0 = 47, a = 28,  b = 40,  angle = 0), 
    fill = kleurB, alpha = 0.75, linewidth = .8
    ),
  annotate(
    "text", 
    x = 75, y = 45, 
    label = expression(italic(B)), 
    color = "black", 
    hjust = 0, 
    size = 5
    )
)

labelAenB <- annotate(
  "text",
  x = 50, y = 50, 
  label = expression(italic(A) ~ "en" ~ italic(B)),
  color = "black",
  size = 5
)

(AB <- kansruimte + A + B + labelAenB)

Figuur 22.3: Venn-diagram met twee gebeurtenissen: \(A\) en \(B\).

In dit geval overlappen de twee cirkels. Dit betekent dat er uitkomsten zijn waarbij \(A\) en \(B\) allebei plaatsvinden.

Het deel van het Venn diagram waar \(A\) en \(B\) overlappen — het cyaan/groenige gedeelte — is zelf óók een gebeurtenis. We noemen deze gebeurtenis “\(A\) en \(B\)”. In de praktijk zijn we vaak geïnteresseerd in de kans op de gebeurtenis “\(A\) en \(B\)”, \(\textrm{Pr}\!\left[A \text{ en } B\right]\). Denk aan de kans dat een willekeurig persoon COPD heeft en rookt, of de kans dat op hetzelfde moment springvloed én noordwesterstorm samenkomen.

Oefening 22.3 (Overlappende gebeurtenissen \(A\) en \(B\), deel 1)

Je gooit één keer met een dobbelsteen. De kansvariabele \(X\) is de uitkomst van dit kansexperiment. We definiëren de volgend gebeurtenissen:

• Gebeurtenis \(A\) is “\(X\) is oneven”,

• Gebeurtenis \(B\) is “\(X\) is groter dan 4”.

Gebruik die definities bij de volgende vragen,

1. Teken Figuur 22.3 na op papier. (Inkleuren hoeft niet.)

2. Bepaal voor elke mogelijke uitkomst (1 tot 6) in welk deel van het Venn-diagram het thuishoort, en schrijf het daarin.

3. Is er een uitkomst waarbij \(A\) en \(B\) beide plaatsvinden?

4. Neem aan dat de dobbelsteen eerlijk is. Wat is de kans \(\textrm{Pr}\!\left[A \text{ en } B\right]\)?

De gebeurtenis “\(A\) of \(B\)”

We zijn ook vaak geïnteresseerd in de situatie dat gebeurtenis \(A\) of gebeurtenis \(B\) plaatsvindt. Dat is de gebeurtenis “\(A\) of \(B\)”. In het Venn-diagram Figuur 22.3 wordt de gebeurtenis “\(A\) of \(B\)” gerepresenteerd door het hele gekleurde gebied, omdat in dat hele gebied ofwel \(A\) ofwel \(B\) plaatsvindt (of beide). De kans op een uitkomst in dat gebied wordt geschreven als \(\textrm{Pr}\!\left[A \textrm{ of } B\right]\).

Inclusieve en exclusieve “of”

Het woord of wordt in het Nederlands op twee manieren gebruikt. Als iemand zegt dat je een koekje of een bonbon mag pakken, mag je meestal niet allebei. Het woord of wordt dan exclusief gebruikt. Maar als je een vaccin mag komen halen als je tot een risicogroep behoort of in de zorg werkt, dan mag dat ook als je tot een risicogroep behoort én in de zorg werkt. Het woord of wordt dan inclusief gebruikt.

In de kansrekening bedoelen we “\(A\) of \(B\)” altijd inclusief: \(A\) vindt plaats, of \(B\), of beide.

Oefening 22.4 (Inclusieve of exclusieve “of”)

Bepaal of “of” in de volgende zinnen inclusief of exclusief bedoeld is. Alle zinnen komen uit de Onderwijs- en Examenregeling (OER) Biologie.

1. “De cursussen van de opleiding hebben een studielast van 7,5 studiepunt of een veelvoud daarvan.”

2. “(…) gedurende de cursus kunnen studenten feedback geven over zaken die mogelijk anders of beter zouden kunnen;”

3. “Als lid of voorzitter van de Examencommissie kan niet benoemd worden iemand die een managementfunctie met financiële verantwoordelijkheid bekleedt (…)”

4. “Het werk van de student wordt beoordeeld op een numerieke schaal of met het oordeel voldoende (V) of onvoldoende (ONV).”

Oefening 22.5 (Overlappende gebeurtenissen \(A\) en \(B\), deel 2)

Gebruik dezelfde definities van \(A\) en \(B\) als in Oefening 22.3. Je kunt ook de schets hergebruiken die je daar hebt gemaakt.

1. Teken een lijn om de gebeurtenis “\(A\) of \(B\)”.

2. Welke uitkomsten vallen onder die gebeurtenis?

3. Aangenomen dat de dobbelsteen eerlijk is, wat is de kans op \(\textrm{Pr}\!\left[A \text{ of } B\right]\)?

22.6 Conditionele kansen

Vaak verandert de kans op een gebeurtenis zodra je extra informatie krijgt. Bijvoorbeeld, de kans dat een persoon zwanger is verandert zodra je leert dat deze persoon 60 jaar oud is. We moeten de kansen op uitkomsten dus herzien wanneer informatie over de uitkomst “gegeven is”. We noemen zulke aangepaste kansen conditionele kansen (conditional probabilities).

De kans op gebeurtenis \(A\) gegeven dat gebeurtenis \(B\) plaatsvindt, wordt geschreven als \[\textrm{Pr}\!\left[A \mid B\right].\] Je spreekt dit uit als “de kans op \(A\) gegeven \(B\)”.

Kijk eens terug naar het Venn-diagram van Figuur 22.3. De kans op \(A\) is de kans op alle uitkomsten binnen de gele cirkel. Maar als gegeven is dat gebeurtenis \(B\) plaatsvindt, dan zijn alle uitkomsten buiten de blauwe cirkel daarmee uitgesloten. De conditionele kans \(\textrm{Pr}\!\left[A \mid B\right]\) is dus de kans op de uitkomsten in het overlappende (cyaan/groenige) gedeelte, dus \(\textrm{Pr}\!\left[A \text{ en } B\right]\), relatief ten opzichte van de kans op de uitkomsten in de gehele blauwe cirkel, dus \(\textrm{Pr}\!\left[B\right]\). Dat levert de volgende formule op: \[\textrm{Pr}\!\left[A \mid B\right] = \frac{\textrm{Pr}\!\left[A \text{ en } B\right]}{\textrm{Pr}\!\left[B\right]}. \qquad(22.2)\]

Oefening 22.6 (Conditionele kansen)

Gebruik weer de definities van Oefening 22.3. Pak het Venn-diagram dat je getekend hebt er ook weer bij.

Ga uit van een eerlijke dobbelsteen.

1. Wat is de kans \(\textrm{Pr}\!\left[A\right]\)?

2. Wat is de kans \(\textrm{Pr}\!\left[B\right]\)?

3. Wat is de kans \(\textrm{Pr}\!\left[A \text{ en } B\right]\)?

4. Wat is de kans op \(\textrm{Pr}\!\left[A \mid B\right]\)?

5. Wat is de kans \(\textrm{Pr}\!\left[B \mid A\right]\)?

6. Leg uit waarom in het algemeen \(\textrm{Pr}\!\left[A \mid B\right]\) niet gelijk is aan \(\textrm{Pr}\!\left[B \mid A\right]\).

Je kunt conditionele kansen vaak interpreteren als kansen voor deelpopulaties. Neem bijvoorbeeld de kans dat een willekeurige Nederlander lijdt aan hartfalen gegeven dat deze persoon diabetes heeft. Dan beperken we ons tot de deelpopulatie van personen met diabetes, en bepalen de kans dat iemand in die deelpopulatie hartfalen heeft.

Oefening 22.7 (Deelpopulaties met hartfalen en/of diabetes)

Nederland telde in 2022 bijna 17,6 miljoen inwoners. Van deze mensen hadden er naar schatting 108 duizend diabetes type 1. Ook hadden er ongeveer 250 duizend een diagnose hartfalen. Er is overlap tussen die groepen: er zijn ongeveer 4 duizend Nederlanders met zowel diabetes type 1 als hartfalen.¹

Stel dat we een willekeurige Nederlander selecteren. Gebeurtenis \(D\) is dat deze persoon diabetes type 1 heeft, gebeurtenis \(H\) dat deze hartfalen heeft.

Gebruik voor onderstaande berekeningen een R-script in plaats van je rekenmachine.

1. Teken op papier een Venn-diagram. Schrijf in ieder “compartiment” van het diagram hoeveel Nederlanders in die categorie vallen.

2. Wat is de kans dat een willekeurig persoon een diagnose hartfalen heeft?

3. Wat is de kans dat een willekeurig persoon diabetes type 1 heeft?

4. Nu beperken we ons tot de deelpopulatie van Nederlanders met diabetes type 1. Wat is de kans dat iemand in die deelpopulatie ook een diagnose hartfalen heeft?

5. Is het risico op hartfalen groter voor patiënten met diabetes type 1 dan voor de doorsnee bevolking? Hoeveel groter?

22.7 De kans op “\(A\) en \(B\)” berekenen

Vaak willen we de kans op \(A\) en \(B\) uitrekenen. Wat zijn de rekenregels die je kunt gebruiken?

Algemene regel voor \(\textrm{Pr}\!\left[A \textrm{ en } B\right]\)

De regel die in alle situaties geldt is:

\[ \textrm{Pr}\!\left[A \textrm{ en } B\right] = \textrm{Pr}\!\left[A \mid B\right]\,\textrm{Pr}\!\left[B\right]. \qquad(22.3)\]

Die regel volgt direct uit Vergelijking 22.2, zoals je zelf kunt verifiëren. Om de kans op \(A\) en \(B\) te berekenen, neem je dus eerst de kans op \(B\), en vermenigvuldigt die met de kans op \(A\) gegeven \(B\).

Omdat \(\textrm{Pr}\!\left[A \textrm{ en } B\right] = \textrm{Pr}\!\left[B \textrm{ en } A\right]\) geldt ook: \[ \textrm{Pr}\!\left[A \textrm{ en } B\right] = \textrm{Pr}\!\left[B \mid A\right]\,\textrm{Pr}\!\left[A\right]. \qquad(22.4)\]

Onafhankelijke gebeurtenissen

Het berekenen van \(\textrm{Pr}\!\left[A \text{ en } B\right]\) is erg eenvoudig als de gebeurtenissen \(A\) en \(B\) onafhankelijk zijn. Laten we dat begrip eerst behandelen.

Twee gebeurtenissen \(A\) en \(B\) zijn onafhankelijk (independent) als de kans op gebeurtenis \(A\) niet verandert wanneer we leren dat gebeurtenis \(B\) plaatsvindt, oftewel, als \[ \textrm{Pr}\!\left[A \mid B\right] = \textrm{Pr}\!\left[A\right]. \qquad(22.5)\] In dat geval verandert ook de kans op \(B\) niet als \(A\) gegeven wordt: \[ \textrm{Pr}\!\left[B \mid A\right] = \textrm{Pr}\!\left[B\right]. \qquad(22.6)\]

Voorbeeld 22.1 (Dobbelstenen: afhankelijke en onafhankelijke gebeurtenissen) Stel je voor dat we twee eerlijke dobbelstenen gooien— eerst een rode, en dan een blauwe. Gebeurtenis \(A\) is dat we met de rode dobbelsteen een zes gooien; gebeurtenis \(B\) dat we met de blauwe dobbelsteen een zes gooien. Zijn \(A\) en \(B\) onafhankelijk?

Het is moeilijk voor te stellen dat de uitkomst van de rode dobbelsteen iets vertelt over de uitkomst van de blauwe dobbelsteen. De uitkomst van de blauwe dobbelsteen hangt minutieus af van de manier waarop hij geworpen wordt; de uitkomst van de rode dobbelsteen zal daarbij geen rol spelen. Het is dus redelijk om aan te nemen dat de gebeurtenissen \(A\) en \(B\) onafhankelijk zijn, als onderdeel van het kansmodel.

En wat als je meerdere keren achter elkaar met dezelfde dobbelsteen gooit? Als je de dobbelsteen tussendoor goed schudt, zullen opeenvolgende uitkomsten ook (vrijwel) onafhankelijk zijn. Maar als je slecht schudt en de dobbelsteen vlak boven de tafel laat vallen, is dat helemaal niet zeker. Dan zijn de voorspellingen van een model dat onafhankelijkheid veronderstelt mogelijk onbetrouwbaar.

Oefening 22.8 (Zijn \(A\) en \(B\) onafhankelijk?)

Kijk eens terug naar Oefening 22.6. Zijn \(A\) en \(B\) daar onafhankelijk?

Vermenigvuldigingsregel voor onafhankelijke gebeurtenissen

We hebben net gezien dat voor onafhankelijke gebeurtenissen Vergelijking 22.5 geldt. Als je die vergelijking invult in de algemene regel Vergelijking 22.3, krijg je de volgende vermenigvuldigingsregel die alleen geldt als \(A\) en \(B\) onafhankelijk zijn: \[ \textrm{Pr}\!\left[A \textrm{ en } B\right] = \textrm{Pr}\!\left[A\right]\textrm{Pr}\!\left[B\right]. \qquad(22.7)\]

Oefening 22.9 (Bloedgroep)

Bloedgroepen worden gekarakteriseerd door de antigenen (O, A, B, of AB) en de rhesusfactor (Rh+ of Rh-). De volgende figuur is van de website van Sanquin:

Figuur 22.4: Verdeling van de bloedgroepen in Nederland. Bron figuur: Sanquin

1. Wat is de kans dat een willekeurig gekozen Nederlander bloedgroep O+ heeft?

2. Wat is de kans dat een willekeurig gekozen Nederlander bloedgroep O heeft (ongeacht de rhesusfactor)?

3. Wat is de kans dat een willekeurig gekozen Nederlander rhesusfactor Rh+ heeft?

4. Als antigen en rhesusfactor onafhankelijk zouden zijn, wat was dan de kans op O+ geweest? Ligt dat ver af van de werkelijkheid? Maken we een grote fout als we in modelberekeningen veronderstellen dat ze onafhankelijk zijn?

5. Wat zou een biologische verklaring kunnen zijn van de grote mate van onafhankelijkheid tussen antigenen en rhesusfactor?

6. Wat vind je van de manier waarop Sanquin de verdeling heeft gevisualiseerd?

22.8 De kans op “\(A\) of \(B\)” berekenen

Nu we rekenregels besproken hebben voor de kans op \(A\) én \(B\) gaan we nu door met formules voor de kans op \(A\) óf \(B\). Dat is gemakkelijk als de gebeurtenissen \(A\) en \(B\) elkaar uitsluiten.

Gebeurtenissen die elkaar uitsluiten

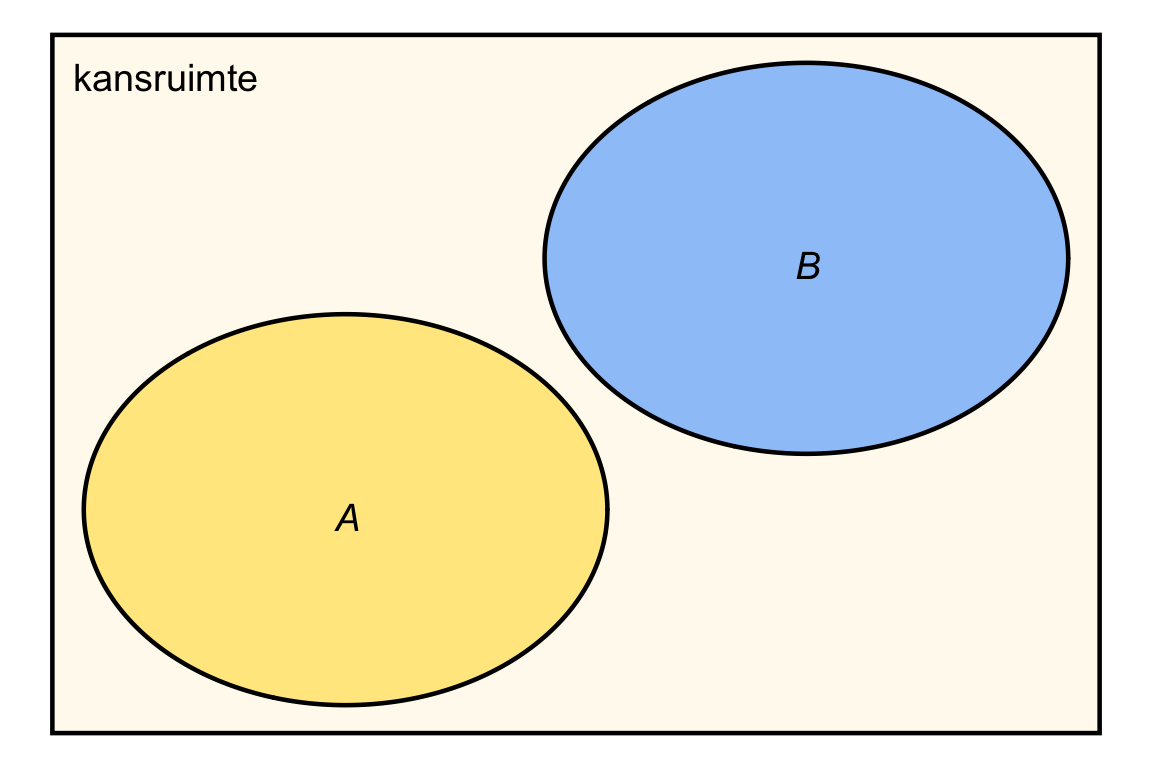
We zeggen dat twee gebeurtenissen \(A\) en \(B\) elkaar uitsluiten als \(A\) en \(B\) niet allebei kunnen plaatsvinden. Dat betekent dat in het Venn-diagram de cirkels voor \(A\) en \(B\) niet overlappen:

A2 <- list(
  geom_ellipse(
    aes(x0 = 28, y0 = 32, a = 25,  b = 28,  angle = 0), 
    fill = kleurA, alpha = 0.5, linewidth = 0.8
    ), 
  annotate(
    "text", 
    x = 27, y = 31, 
    label = expression(italic(A)), 
    color = "black", 
    hjust = 0, 
    size = 5
    )
  )

B2 <- list(
  geom_ellipse(
    aes(x0 = 72, y0 = 68, a = 25,  b = 28,  angle = 0), 
    fill = kleurB, alpha = 0.5, linewidth = 0.8
    ),
  annotate(
    "text", 
    x = 71, y = 67, 
    label = expression(italic(B)), 
    color = "black", 
    hjust = 0, 
    size = 5
    )
)

(AB2 <- kansruimte + A2 + B2)

Figuur 22.5: Venn-diagram. De gebeurtenissen \(A\) en \(B\) overlappen niet en sluiten elkaar dus uit.

Dan geldt ook dat \(\textrm{Pr}\!\left[A \mid B\right] = 0\) en \(\textrm{Pr}\!\left[B \mid A\right] = 0\), want gegeven dat \(B\) plaatsvindt is gebeurtenis \(A\) onmogelijk, en andersom.

Optelregel voor gebeurtenissen die elkaar uitsluiten

Als twee gebeurtenissen \(A\) en \(B\) elkaar uitsluiten geldt de volgende optelregel: \[ \textrm{Pr}\!\left[A \textrm{ of } B\right] = \textrm{Pr}\!\left[A\right] + \textrm{Pr}\!\left[B\right]. \qquad(22.8)\]

Als gebeurtenissen elkaar niet uitsluiten, kun je Vergelijking 22.8 niet gebruiken.

Oefening 22.16 (Welke redeneringen hieronder kloppen?)

1. Bij een gokspelletje heb ik iedere keer dat ik meedoe een kans van \(\frac{1}{10}\) om een prijs te winnen.

   Als ik twee keer meedoe is de kans dat ik een prijs win:

   \[ \begin{align} \textrm{Pr}\!\left[\text{1e keer prijs}\right] + \textrm{Pr}\!\left[\text{2de keer prijs}\right] &= \frac{1}{10} + \frac{1}{10} \\ &= \frac{2}{10}. \end{align} \]

2. De kans dat de bloedgroep van een willekeurige person rhesusfactor + heeft, is: \[ \textrm{Pr}\!\left[\text{+}\right]= \textrm{Pr}\!\left[\text{O+}\right] + \textrm{Pr}\!\left[\text{A+}\right] + \textrm{Pr}\!\left[\text{B+}\right] + \textrm{Pr}\!\left[\text{AB+}\right]. \]

Algemene regel

De regel voor als \(A\) en \(B\) elkaar niet uitsluiten kun je begrijpen met behulp van het Venn-diagram:

AB

Figuur 22.6: Venn-diagram. Voor de kans op \(A\) of \(B\) moet het overlappende (groenige) gebied één keer worden meegeteld!

De kans op \(A\) of \(B\) is de kans op alle uitkomsten in de gele en de blauwe cirkel. Als je de kans op \(A\) (de kans binnen de gele cirkel) en de kans op \(B\) (de kans binnen de blauwe cirkel) optelt, dan tel je de kans binnen het overlappende gebied (het groenige gebied) dubbel. Daarom moet je die kans er één keer vanaf trekken. Die kans is precies de kans op \(A\) én \(B\). Het algemene formule is daarom:

\[ \textrm{Pr}\!\left[A \textrm{ of } B\right] = \textrm{Pr}\!\left[A\right] + \textrm{Pr}\!\left[B\right] - \textrm{Pr}\!\left[A \textrm{ en } B\right]. \qquad(22.9)\]

Oefening 22.10 (Optelregel of algemene regel)

Stel dat \(A\) en \(B\) elkaar wederzijds uitsluiten.

1. Wat is \(\textrm{Pr}\!\left[A \textrm{ en } B\right]\) dan?

2. Als \(A\) en \(B\) elkaar uitsluiten mag je de optelregel Vergelijking 22.8 gebruiken om \(\textrm{Pr}\!\left[A \textrm{ of } B\right]\) te berekenen. Gaat er iets mis als je in plaats daarvan de algemene regel Vergelijking 22.9 gebruikt?

Oefening 22.11 (Resistente bacterien)

In een populatie bacteriën komen twee mutaties voor die de bacterie resistent maken tegen het antibioticum ciprofloxacin.

Mutatie 1 komt voor in 30% van de bacteriën, mutatie 2 in 40% van de bacteriën. Maar, er is overlap: 15% van de bacteriën heeft beide mutaties.

Welk percentage van de bacteriën is resistent?

Oefening 22.12 (De kans op \(A\) of \(B\) of \(C\))  

1. Teken een Venn-diagram met daarin drie gebeurtenissen: \(A\), \(B\), en \(C\). Zorg ervoor dat alle gebeurtenissen overlap met elkaar hebben, en dat er ook een plek is waar ze alle drie overlappen.

2. De formule voor de kans op \(A\) of \(B\) of \(C\) begint met het optellen van de kansen op \(A\), \(B\), en \(C\):

   \[\textrm{Pr}\!\left[A \text{ of } B \text{ of } C\right] = \textrm{Pr}\!\left[A\right] + \textrm{Pr}\!\left[B\right] + \textrm{Pr}\!\left[C\right] + \ldots\]

   Wat moet er op de puntjes worden ingevuld?

   Hint: Bekijk je Venn-diagram en bepaal welke delen dubbel of zelfs driedubbel worden geteld.

22.9 De Stelling van Bayes

In Oefening 22.6 heb je gezien dat \(\textrm{Pr}\!\left[A \mid B\right]\) en \(\textrm{Pr}\!\left[B \mid A\right]\) meestal niet gelijk zijn. Bijvoorbeeld: de kans dat iemand Engels verstaat gegeven dat hij Nederlander is, is iets heel anders dan de kans dat iemand Nederlander is gegeven dat hij Engels verstaat.

Toch is er wel een relatie tussen de twee conditionele kansen. Die relatie heet de Stelling van Bayes (Bayes’ Theorem) of de regel van Bayes (Bayes’ rule), naar Thomas Bayes (1701–1761), de Engelse predikant en wiskundige die deze regel als eerste lijkt te hebben gebruikt.

De regel van Bayes kan gemakkelijk worden afgeleid uit twee vergelijkingen die we eerder gezien hebben, namelijk Vergelijking 22.3 en Vergelijking 22.4: \[ \begin{gather} \textrm{Pr}\!\left[A \text{ en } B\right] = \textrm{Pr}\!\left[ B \mid A\right]\textrm{Pr}\!\left[A\right],\\ \textrm{Pr}\!\left[A \text{ en } B\right] = \textrm{Pr}\!\left[ A \mid B\right]\textrm{Pr}\!\left[B\right]. \end{gather} \] Daaruit volgt dat \[ \textrm{Pr}\!\left[ B \mid A\right]\textrm{Pr}\!\left[A\right] = \textrm{Pr}\!\left[ A \mid B\right]\textrm{Pr}\!\left[B\right]. \] Aangenomen dat \(\textrm{Pr}\!\left[A\right] \neq 0\) kunnen we vervolgens delen door \(\textrm{Pr}\!\left[A\right]\), en daarmee krijgen we de gewenste regel:

Important 22.1: De Stelling van Bayes

\[ \textrm{Pr}\!\left[ B \mid A\right] = \frac{\textrm{Pr}\!\left[A \mid B\right] \textrm{Pr}\!\left[B\right]}{\textrm{Pr}\!\left[A\right]}. \qquad(22.10)\]

Deze stelling maakt het mogelijk om \(\textrm{Pr}\!\left[B \mid A\right]\) en \(\textrm{Pr}\!\left[A \mid B\right]\) in elkaar om te rekenen.

Oefening 22.13 (De kans op diabetes gegeven hartfalen)

Kijk eens terug naar Oefening 22.7. Je hebt daar verschillende kansen uitgerekend, waaronder de kans \(\textrm{Pr}\!\left[H \mid D\right]\) dat iemand met diabetes type 1 ook een diagnose hartfalen heeft.

Gebruik nu de Stelling van Bayes om \(\textrm{Pr}\!\left[D \mid H\right]\) uit te rekenen, de kans dat een willekeurig persoon met een diagnose hartfalen ook diabetes type 1 heeft. Maak bij de berekening gebruik van je resultaten uit Oefening 22.7.

22.10 Samenvatting

Basisbegrippen & frequentistische definities

Kansrekenen gaat over kansexperimenten. Een kansexperiment kan meerdere uitkomsten hebben. Iedere functie van de uitkomst is een kansvariabele. De verzameling van mogelijke uitkomsten heet de kansruimte. Een gebeurtenis is een deelverzameling van de kansruimte. Volgens de frequentistische definitie is de kans op een gebeurtenis de relatieve frequentie waarmee de gebeurtenis voorkomt in een oneindige reeks herhalingen van hetzelfde kansexperiment.

Om kansen te kunnen berekenen voor gebeurtenissen in de werkelijkheid moet je altijd aannames maken over het kansexperiment: een kansmodel.

Venn-diagrammen

Een Venn-diagram is een diagram waarin de kansruimte en relevante gebeurtenissen verbeeld worden als vormen (zoals cirkels) met of zonder overlap.

Rekenregels

Som van alle kansen

Bij categorische variabelen en discrete variabelen kunnen de kansen worden opgeteld: \[ \sum_x \textrm{Pr}\!\left[X = x\right] = 1. \] De sommatie gaat over alle mogelijke uitkomsten \(x\) (de volledige kansruimte).

Complementregel

\[ \textrm{Pr}\!\left[A\right] = 1 - \textrm{Pr}\!\left[ \text{niet } A\right].\]

Conditionele kansen

De kans op \(A\) gegeven \(B\): \[\textrm{Pr}\!\left[A \mid B\right] = \frac{\textrm{Pr}\!\left[A \text{ en } B\right]}{\textrm{Pr}\!\left[B\right]}.\] Gebeurtenissen \(A\) en \(B\) zijn onafhankelijk als: \[ \textrm{Pr}\!\left[A \mid B\right] = \textrm{Pr}\!\left[A\right].\]

Kans op A en B

Vermenigvuldigingsregel voor onafhankelijke gebeurtenissen: \[ \textrm{Pr}\!\left[A \textrm{ en } B\right] = \textrm{Pr}\!\left[A\right] \textrm{Pr}\!\left[B\right]. \]

Algemene regel: \[ \textrm{Pr}\!\left[A \textrm{ en } B\right] = \textrm{Pr}\!\left[A \mid B\right]\textrm{Pr}\!\left[B\right]. \]

Kans op A of B

Optelregel voor gebeurtenissen die elkaar uitsluiten: \[ \textrm{Pr}\!\left[A \textrm{ of } B\right] = \textrm{Pr}\!\left[A\right] + \textrm{Pr}\!\left[B\right]. \]

Algemene regel: \[ \textrm{Pr}\!\left[A \textrm{ of } B\right] = \textrm{Pr}\!\left[A\right] + \textrm{Pr}\!\left[B\right] - \textrm{Pr}\!\left[A \textrm{ en } B\right]. \]

Stelling van Bayes

\[ \textrm{Pr}\!\left[ B \mid A\right] = \frac{\textrm{Pr}\!\left[A \mid B\right] \textrm{Pr}\!\left[B\right]}{\textrm{Pr}\!\left[A\right]}. \]

22.11 Terminologie

Tabel 22.1: Woordenlijst Hoofdstuk 22 .

Nederlands	Engels	Betekenis
conditionele kans	conditional probability	De kans op een gebeurtenis als gegeven dat een andere gebeurtenis plaatsvindt.
frequentistisch kansbegrip	frequentist probability concept	Begrippenkader waarbinnen een kans gedefineerd wordt als de relatieve frequentie in een oneindige reeks identiek uitgevoerde kansexperimenten.
gebeurtenis	event	Een deelverzameling van mogelijke uitkomst van een kansexperiment.
kansexperiment	chance experiment	Een experiment of procedure waarbij de uitkomst niet van tevoren te voorspellen is.
kansruimte	sample space	De verzameling van alle mogelijke uitkomsten van een kansexperiment.
kansvariabele	random variable	Een variabele waarvan de waarde afhangt van de uitkomst van een kansexperiment.
onafhankelijk gebeurtenissen	independent events	Twee gebeurtenissen zijn onafhankelijk als de kans op de ene gebeurtenis niet verandert als gegeven wordt dat de andere plaatsvindt.
stochastische variabele/stochast	stochastic variable	Een ander woord voor kansvariabele.
Venn-diagram	Venn diagram	Een diagram waarin de kansruimte en relevante gebeurtenissen verbeeld worden als vormen (zoals cirkels) met of zonder overlap.

22.12 Opgaven

Oefening 22.14 (Eenvoudig model voor de lengtes van G-tracts)

Een DNA-sequentie die alleen uit de letter G bestaat, wordt een G-tract genoemd. In het DNA van veel organismen komen lange G-tracts voor. Dat kan natuurlijk toeval zijn. De vraag komt dus op: Hoe lang verwachten we dat G-tracts zoal zijn?

Om onze verwachting te kalibreren stellen we een model op. We noemen de fractie van de nucleotiden dat een G is \(p\). Ons model is nu dat iedere letter van een genoom onafhankelijk met kans \(p\) een G is en dus met kans \(1 - p\) C,T, of A.

In werkelijkheid is een genoom natuurlijk niet random samengesteld, maar dit model kan wel iets vertellen over wat we bij toeval kunnen verwachten.

1. Stel dat we ergens in een DNA-sequentie een G tegenkomen. Wat is volgens het model de kans dat direct daarna een C,T, of A volgt?

   Merk op dat dit de kans is dat een G-tract lengte 1 heeft, \(\textrm{Pr}\!\left[X = 1\right]\).

2. Stel dat we ergens in een DNA-sequentie een G tegenkomen. Wat is volgens het model de kans dat er daarna eerst nog een G volgt, en daarna een C,T, of A?

   Merk op dat dit de kans is dat een G-tract lengte 2 heeft, \(\textrm{Pr}\!\left[X = 2\right]\).

3. Stel dat we ergens in een DNA-sequentie een G tegenkomen. Wat is volgens het model de kans dat er daarna eerst nog twee keer een G volgt, en daarna een C,T, of A?

   Merk op dat dit de kans is dat een G-tract lengte 3 heeft, \(\textrm{Pr}\!\left[X = 3\right]\).

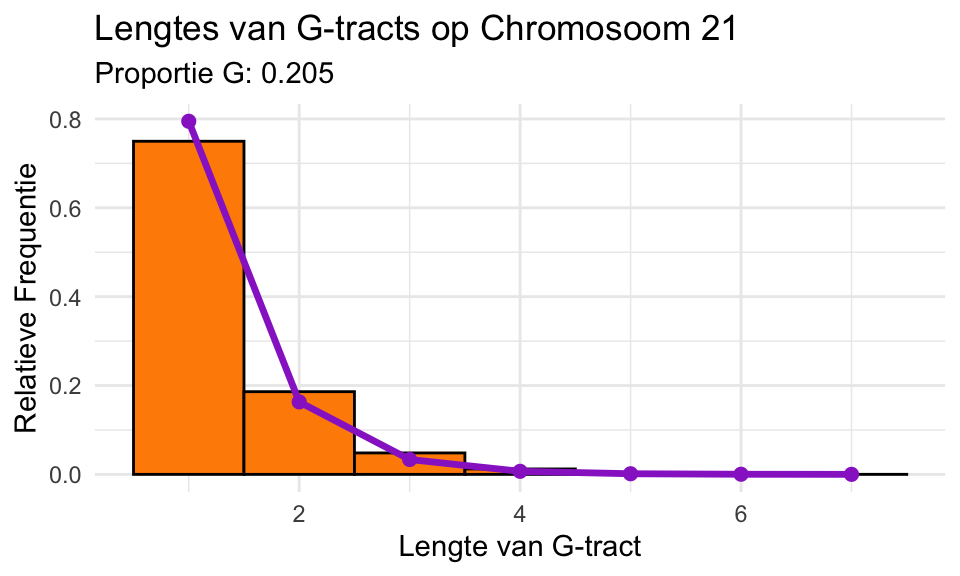
4. Als voorbeeld gebruiken we het humaan chromosoom 21. Voor dat chromosoom is de fractie G gelijk aan \(p = 0{,}205\). Bereken \(\textrm{Pr}\!\left[X =1\right]\), \(\textrm{Pr}\!\left[X = 2\right]\), en \(\textrm{Pr}\!\left[X = 3\right]\) voor die waarde van \(p\). (Als je zin hebt, kun je ook \(\textrm{Pr}\!\left[X = 4\right]\) en verder uitrekenen!)

5. Om de daadwerkelijke verdeling van lengtes van G-tracts te bepalen, hebben we de sequentie van chromosoom 21 (46709983 nucleotiden) gedownload en een R-script geschreven om de verdeling te bepalen.

   Het resultaat is:²

   # Controleer of benodigde packages geladen zijn
   if (!("ggplot2" %in% .packages())) { library(ggplot2) }
   if (!("httr" %in% .packages())) { library(httr) }
   if (!("R.utils" %in% .packages())) { library(R.utils) }
   if (!("dplyr" %in% .packages())) { library(dplyr) }
   
   # ---- Stap 1: Lees het genoom vanuit het gedownloade FASTA-bestand ----
   
   # Path naar het FASTA-bestand
   #fasta_bestand <- "data/Homo_sapiens.GRCh38.dna.chromosome.21.fa"
   fasta_bestand <- "https://tbb.bio.uu.nl/hermsen/DataStatistiek/Homo_sapiens.GRCh38.dna.chromosome.21.fa"
   
   # Lees het FASTA-bestand als tekstregels
   fasta_regels <- readLines(fasta_bestand)
   
   # Verwijder de header-regel(s) (die beginnen met ">")
   dna_regels <- fasta_regels[!grepl("^>", fasta_regels)]
   
   # Concateneer alle regels tot één lange DNA-string
   dna <- paste(dna_regels, collapse = "")
   
   # ---- Stap 2: Identificeer G-tracts ----
   
   # Regex om G-tracts te vinden (continue stukken van 'G')
   g_tracts <- gregexpr("G+", dna, perl = TRUE)[[1]]
   
   # Lengtes van de gevonden G-tracts
   lengtes_g_tracts <- attr(g_tracts, "match.length")
   
   # Filter lege waarden en beperk tot lengte <= 7
   lengtes_g_tracts <- lengtes_g_tracts[
     lengtes_g_tracts > 0 & lengtes_g_tracts <= 7
   ]
   
   # ---- Stap 3: Bepaal de correcte GC-content en p_G ----
   
   # Tellen van alleen A, T, C, G (N wordt genegeerd)
   nucleotiden <- table(strsplit(dna, NULL)[[1]])
   nucleotiden <- nucleotiden[
     names(nucleotiden) %in% c("A", "T", "C", "G")
   ]
   
   # Totale geldige bases
   aantal_valid <- sum(nucleotiden)
   
   # GC-content
   gc_gehalte <- (nucleotiden["G"] + nucleotiden["C"]) / aantal_valid
   
   # Kans op een 'G' in een willekeurig gekozen positie
   p_g <- nucleotiden["G"] / aantal_valid
   
   # ---- Stap 4: Bereken de verwachte geometrische verdeling ----
   
   # Geometrische verdeling: (1 - p_G) * p_G^(k-1) * totaal aantal waarnemingen
   max_lengte <- 7
   verwachte_frequenties <- data.frame(
     lengte = 1:max_lengte,
     frequentie = (1 - p_g) * p_g^(0:(max_lengte - 1)) *
                  length(lengtes_g_tracts)
   )
   
   # ---- Stap 5: Bereken de relatieve frequenties ----
   
   # Dataframe maken voor waargenomen verdeling
   data_g_tracts <- as.data.frame(table(lengtes_g_tracts))
   colnames(data_g_tracts) <- c("lengte", "absolute_frequentie")
   
   # Zet lengte om naar numeriek
   data_g_tracts$lengte <- as.numeric(as.character(data_g_tracts$lengte))
   
   # Bereken relatieve frequentie
   data_g_tracts$relatieve_frequentie <-
     data_g_tracts$absolute_frequentie /
     sum(data_g_tracts$absolute_frequentie)
   
   # Normaliseer de verwachte verdeling naar relatieve frequentie
   verwachte_frequenties$frequentie <-
     verwachte_frequenties$frequentie /
     sum(verwachte_frequenties$frequentie)
   
   # ---- Stap 6: Plot de relatieve frequenties ----
   
   ggplot(data_g_tracts, aes(x = lengte, y = relatieve_frequentie)) +
     geom_bar(
       stat = "identity", fill = "darkorange", color = "black",
       alpha = 1, width = 1
     ) +
     geom_line(
       data = verwachte_frequenties, aes(x = lengte, y = frequentie),
       color = "DarkOrchid", size = 1.2
     ) +
     geom_point(
       data = verwachte_frequenties, aes(x = lengte, y = frequentie),
       color = "DarkOrchid", size = 2
     ) +
     labs(
       title = "Lengtes van G-tracts op Chromosoom 21",
       subtitle = paste("Proportie G:", round(p_g, 3)),
       x = "Lengte van G-tract",
       y = "Relatieve Frequentie"
     ) +
     theme_minimal()

   

   Het histogram geeft de echte data weer, en de paarse lijn is de verwachting op basis van ons eenvoudige model.

   Vergelijk het histogram met de paarse lijn. Wat is jouw conclusie?

Oefening 22.15 (De screening-paradox)

Bij bevolkingsonderzoeken worden mensen gescreend om ziektes in een vroeg stadium te ontdekken. Bijvoorbeeld, in de strijd tegen borstkanker worden in Nederland vrouwen van 50 tot 75 jaar elke twee jaar uitgenodigd voor een mammografie.

De sensitiviteit van een mammografie is ongeveer 90%; dat wil zeggen dat de kans 0,9 is dat de test positief is als een vrouw daadwerkelijk borstkanker heeft. De specificiteit van een mammografie is ongeveer 95%; dat wil zeggen dat de kans 0,95 is dat de test negatief uitvalt bij vrouwen die geen borstkanker hebben. Een mammografie is dus een behoorlijk sensitieve en specifieke test, en bovendien niet duur.

Borstkanker komt ook voor bij jongere vrouwen, met akelige consequenties. De vraag rijst dan: waarom screenen we jongere vrouwen niet?

Dit heeft te maken met de screening-paradox; deze opgave illustreert het probleem

Laten we als voorbeeld bekijken wat er zou gebeuren als we alle vrouwen van 30 jaar zouden screenen. Dat zijn er in Nederland zo’n 120 000. Schattingen geven aan dat ongeveer 0,1% van de vrouwen van die leeftijd borstkanker heeft. (We noemen dat getal de prevalentie van borstkanker op die leeftijd.)

De gebeurtenis dat een willekeurige vrouw van 30 borstkanker heeft noteren we als \(K\), de gebeurtenis dat ze geen borstkanker heeft als \(G\) (voor gezond). De gebeurtenis van een positieve test is \(P\) en die van een negatieve test is \(N\).

1. Wat is \(\textrm{Pr}\!\left[K\right]\)? Hoeveel vrouwen van 30 jaar hebben dus naar verwachting borstkanker?

2. Wat is \(\textrm{Pr}\!\left[G\right]\)? Hoeveel vrouwen van 30 jaar hebben géén borstkanker?

3. Wat is \(\textrm{Pr}\!\left[P \mid K\right]\)? Bij hoeveel vrouwen zou de screening naar verwachting kanker ontdekken?

4. Wat is \(\textrm{Pr}\!\left[N \mid G\right]\)?

5. Wat is \(\textrm{Pr}\!\left[P \mid G\right]\)? Bij hoeveel vrouwen zou de screening naar verwachting onterecht positief uitvallen? Vergelijk dit met je antwoord op onderdeel c.

6. Wat is \(\textrm{Pr}\!\left[P\right]\), de kans dat een willekeurige vrouw een positieve test krijgt? Hint: gebruik dat \[ \begin{align} \textrm{Pr}\!\left[P\right] &= \textrm{Pr}\!\left[K \text{ and } P\right] + \textrm{Pr}\!\left[G \text{ and } P\right]\\ & = \textrm{Pr}\!\left[P \mid K\right]\textrm{Pr}\!\left[K\right] + \textrm{Pr}\!\left[P \mid G\right]\textrm{Pr}\!\left[G\right].\\ \end{align} \] Hoeveel vrouwen krijgen dus in totaal een positieve test terug?

7. Wat is \(\textrm{Pr}\!\left[K \mid P\right]\), de kans dat iemand die met een positieve test wordt doorverwezen naar de oncoloog ook daadwerkelijk kanker heeft?

   Hint: gebruik de Stelling van Bayes.

8. Wat is, gezien deze resultaten, het grote nadeel van vroegtijdig screenen?

9. De sensitiviteit en specificiteit van deze test was behoorlijk hoog; toch hebben de meeste vrouwen met een positieve uitslag geen kanker. Dat gegeven wordt de screening-paradox genoemd. Leg uit wanneer die paradox optreedt.

---

1. Vanhommerig, Joost, and Bart Knottnerus. “Diabetes mellitus type 1 en type 2 in Nederland: comorbiditeit in 2022,” 2022.

2. Als je wilt, kun je het resultaat namaken door het script te kopieren en op je eigen computer te runnen. Je moet dan wel zelf de datafile voor chromosoom 21 even hier downloaden, en zorgen dat het pad in de code naar jouw bestand verwijst.