20  Variabelen en hun verdelingen

20.1 Leerdoelen

Na het bestuderen van dit hoofdstuk:

• kun je de verschillende typen variabelen onderscheiden;
• weet je wat de verdeling en cumulatieve verdeling van een variabele is;
• kun je verdelingen omschrijven met veelgebruikte termen;
• kun je verschillende centrum- en spreidingsmaten berekenen en interpreteren;
• kun je verdelingen samenvatten in frequentietabellen;
• weet je hoe je verschillende typen gegevens kunt visualiseren met grafieken en diagrammen.

20.2 Beschrijvende statistiek

Je hebt maandenlang in het lab gestaan, en het resultaat is een Excel-bestand met een enorme verzameling getallen. Je begrijpt dat je in de cijferbrij patronen moet ontdekken, maar je ziet door de bomen het bos niet meer. Wat nu?

Beschrijvende statistiek (descriptive statistics) is het onderdeel van de statistiek dat zich bezighoudt met methoden en technieken voor het creëren van overzicht in gegevens.

In de praktijk kunnen de gebruikte technieken worden onderverdeeld in drie categorieën.

1. Kengetallen berekenen. Met kengetallen bedoelen we getallen die een reeks gegevens karakteriseren. Een voorbeeld is het gemiddelde; dat typeert hoe groot de waarden in je reeks getallen zoal zijn. Kengetallen worden ook wel statistieken (statistics) genoemd.

2. Samenvatten in tabellen, zoals frequentietabellen of kruistabellen. Vaak zijn die veel overzichtelijker dan de lange lijst met individuele gegevens.

3. Visualiseren met grafieken en diagrammen. Ons visueel systeem is enorm goed in het analyseren van beelden van objecten in de ruimte. Het idee van grafieken is om grootheden die eigenlijk helemaal geen ruimtelijke eigenschappen voorstellen, zoals gewicht of temperatuur, weer te geven als de coördinaten, vormen, kleuren, of maten van inktpatronen op papier. Structuur in de gegevens kan zo met het oog worden ontdekt.

Deze drie categorieën — kengetallen, tabellen, visualisaties — komen hieronder allemaal aan bod. Je zult zien dat ze sterk met elkaar samenhangen.

Maar hoe je gegevens kunt beschrijven hangt af van het soort gegevens. Daarom moeten we eerst stilstaan bij de verschillende typen gegevens die je kunt tegenkomen.

20.3 Verschillende soorten variabelen

Een dataset is een verzameling meetwaarden of observaties van eigenschappen. Die eigenschappen worden variabelen genoemd. Bijvoorbeeld, mutanten van Drosophila (fruitvliegen) kunnen verschillende kleuren ogen hebben; oogkleur is dus een variabele. Andere voorbeelden zijn het aantal eieren in een vogelnest, de dikte van een jaarring in een boomstam, of de beoordeling van een hotel (1 tot 5 sterren).

Het is nuttig om variabelen in te delen in categorieën. Een veelgebruikte indeling is weergegeven in Figuur 20.1.

flowchart TB
  A(Variabelen) --> B("Numeriek (Kwantitatief)")
  A --> C("Categorisch (Kwalitatief)")
  B --> F(Discreet)
  B --> G(Continu)
  C --> E(Nominaal)
  C --> D(Ordinaal)

Figuur 20.1: Indeling van typen variabelen.

Het diagram maakt eerst onderscheid tussen numerieke en categorische variabelen.

Numerieke variabelen (numerical) stellen meetbare hoeveelheden voor, uitgedrukt in een getal. Voorbeelden zijn het aantal dendrieten aan een neuron, of de concentratie van cortisol in het speeksel van een varken. Numerieke variabelen worden ook wel kwantitatieve variabelen genoemd.

Categorische variabelen (categorical) hebben waarden die een categorie of groep aanduiden. Ze stellen geen meetbare hoeveelheden voor; je kunt ze dus ook niet optellen of aftrekken. De mogelijke waarden worden niveaus (levels) genoemd. Voorbeelden van categorische variabelen zijn

• de genus van bacteriën betrokken bij een blaasontsteking, met niveaus Escherichia, Klebsiella, etc.
• kankerstadia, met niveaus 0, I, II, III, of

Categorische variabelen worden ook wel kwalitatieve variabelen genoemd.

Niet alle getallen zijn numeriek

Dat kankerstadium wordt uitgedrukt in een (Romeins) getal (0, I, II, III, of IV) wil niet zeggen dat het een numerieke variabele is. Het getal stelt namelijk geen meetbare hoeveelheid voor, en het optellen van kankerstadia is onzinnig. We hadden de stadia net zo goed kunnen aanduiden met letters A, B, C, D, en E.

Binnen de numerieke variabelen onderscheiden we discrete en continue variabelen. Een variabele is discreet als deze alleen specifieke, afzonderlijke waarden kan aannemen. Dit is bijvoorbeeld het geval bij tellingen, zoals het aantal plantensoorten dat je op een vierkante meter heidegrond aantreft: deze variabele kan alleen gehele getallen aannemen (0, 1, 2, …). Een numerieke variabele is continu als deze in theorie elke waarde uit een interval van reële getallen kan aannemen. Een voorbeeld hiervan is lichaamsgewicht, omdat een gewicht in principe elk positieve reële waarde kan aannemen, zoals 86,143875 kg of zelfs 20\(\pi\) kg.

Tijd als continue of discrete variabele

In de Introductie van het onderdeel Biologische modellen ben je het verschil tussen continue en discrete variabelen al tegengekomen toen de verschillen tussen differentievergelijkingen en differentiaalvergelijkingen werden uitgelegd. Het belangrijkste verschil was of de variabele tijd als een discrete of als een continue variabele werd behandeld.

Binnen de categorische variabelen onderscheiden we ordinale en nominale variabelen. Bij ordinale variabelen hebben de niveaus een natuurlijke volgorde. De kankerstadia (0, I, II, III, IV) zijn weer een goed voorbeeld. Bij nominale variabelen hebben de niveaus géén natuurlijke rangorde. Het zijn enkel namen of labels. Een voorbeeld is de voedingsstrategie van organismen, met als niveaus “herbivoor”, “carnivoor”, “omnivoor”, of “detrivoor”.

Alternatieve indelingen van variabelen

De indeling van Figuur 20.1 is niet de enige manier waarop variabelen kunnen worden ingedeeld. Over andere indelingen kun je meer lezen in het artikel Statistical data type op Wikipedia.

Oefening 20.1 (Typen variabelen.)
Van welk type zijn de volgende variabelen?

1. Bloedgroep (A, B, AB, of O).

2. Aantal chromosomen in een cel.

3. Opleidingsniveau. Het Centraal Bureau voor de Statistiek (CBS) hanteert vaak 5 niveaus:

   Tabel 20.1: Onderwijsniveaus gebruikt door het CBS.

   Onderwijsniveau	Omschrijving
   1	Basisonderwijs
   2	Vmbo, havo-, vwo-onderbouw, mbo1
   3	Havo, vwo, mbo2-4
   4	Hbo-, wo-bachelor
   5	Hbo-, wo-master, doctor

4. Hartslagfrequentie.

5. Verdubbelingstijd van een bacteriekolonie.

6. Fitness, gemeten als het aantal nakomelingen van een organisme in de volgende generatie.

Oefening 20.2 (Variabelen in de dataset NHANES van de US National Center for Health Statistics)
Om de theorie in dit hoofdstuk te illustreren zullen we vaak gebruik maken van een dataset met de naam NHANES. Deze dataset is samengesteld door het US National Center for Health Statistics (NCHS). Jaarlijks onderzoekt het NCHS de gezondheid van ongeveer 5000 Amerikanen van alle leeftijden. De NHANES dataset bevat de gegevens van een groot aantal personen die tussen 2009 en 2012 zijn onderzocht.

Je kunt de dataset ook gemakkelijk zelf onderzoeken met R.

1. De dataset is beschikbaar via een R-package met de naam NHANES. Installeer dat package, met het commando:

   install.packages("NHANES", dependencies = TRUE)

2. Start een nieuw R-script. Kopieer onderstaande code en plak die in je script.

   library("NHANES") # laad de library 
   data("NHANES") # laad de dataset "NHANES" in een dataframe
   View(NHANES)   # open een tab in RStudio om de dataframe te bekijken

   Zorg dat je begrijpt waar de verschillende regels code goed voor zijn en voer ze dan uit.

3. Bekijk de gegevens in RStudio. (Met het commando View(NHANES) is een tab geopend waar je door de gegevens heen kunt scrollen.) De dataset bestaat uit een groot aantal regels en kolommen. Iedere regel beschrijft één persoon; iedere kolom bevat de informatie voor één variabele.

   Een van de variabelen is burgerlijke staat (MaritalStatus). Zoek die kolom op.

   • Van welk type is deze variabele volgens het systeem van Figuur 20.1?
   • Wat zijn de niveaus?

4. Zoek ook de kolom voor variabele lichaamslengte (Height).

   • Van welk type is deze variabele?
   • Welke eenheid wordt gebruikt?

   (Tip: Bij twijfel gebruik je het commando ?NHANES om de Help-files te bekijken; daar staat voor iedere variabele informatie.)

5. Zoek de kolom voor nBabies. Voor iedere vrouw vanaf 20 jaar is daar het aantal baby’s weergegeven dat zij op de wereld heeft gezet.

   • Van welk type is deze variabele?
   • Wat is er bij mannen ingevuld?
   • Wat is er bij vrouwen ingevuld als zij geen babies hebben?

6. Voer het volgende commando toe aan je script en voer het uit:

   str(NHANES)

   De functie str() geeft de structuur van het data frame weer.

   • Van hoeveel personen is er informatie opgenomen in deze dataset?
   • Hoeveel variabelen zijn er?

20.4 De verdeling van een variabele

In de praktijk willen we vaak weten hoe de waarden van een variabele over de mogelijke waarden zijn verspreid. We noemen dat de verdeling (distribution) van de variabele.

Histogrammen

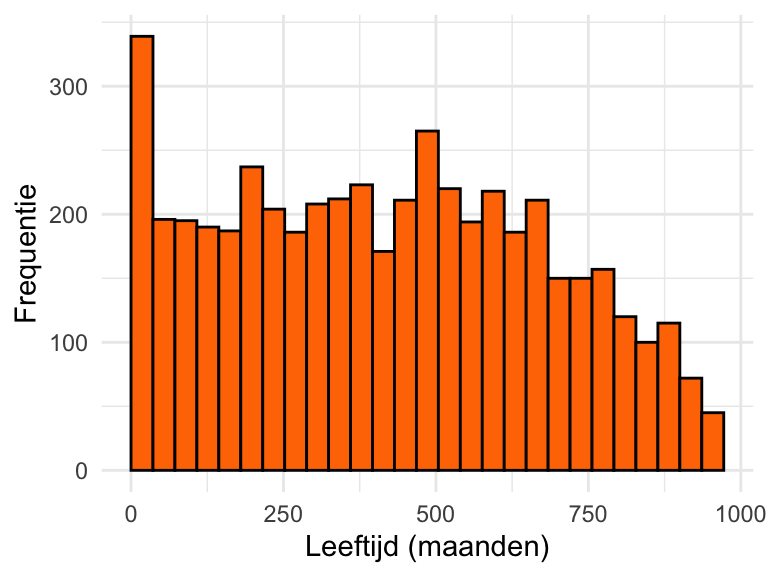
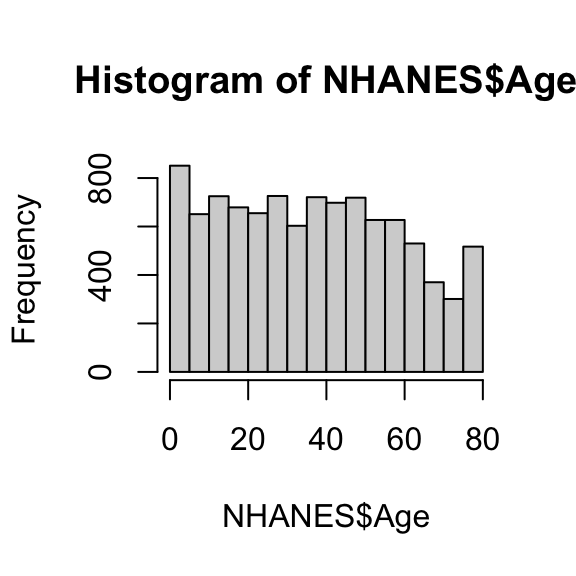
Als de variabele numeriek is, kunnen we zijn verdeling visualiseren met een histogram. Figuur 20.2 hieronder laat een voorbeeld zien voor variabele AgeMonths (leeftijd in maanden) uit de dataset NHANES die we in Oefening 20.2 hebben bekeken

# Controleer of ggplot2 en NHANES zijn geladen
if (!("ggplot2" %in% .packages())) { 
  library(ggplot2) 
}
if (!("NHANES" %in% .packages())) { 
  library(NHANES) 
}

data("NHANES")

ggplot(
  data = NHANES, 
  aes(x = AgeMonths)
  ) +
  geom_histogram(
    fill = opvulkleur, 
    color = "black",
    binwidth = 36,
    boundary = 0,
    closed = "left"
    ) +
  labs(title = NULL,
    x = "Leeftijd (maanden)",
    y = "Frequentie"
  ) +
  theme_minimal()

Figuur 20.2: Histogram van leeftijd in de dataset NHANES.

Een histogram is opgebouwd uit staafjes. De hoogte van die staafjes geeft weer hoe vaak een leeftijd binnen een bepaalde leeftijdscategorie valt; dat wordt de frequentie van die categorie genoemd. We komen in Paragraaf 20.12.1 uitgebreider terug op histogrammen en andere manieren om verdelingen te visualiseren.

Kwalitatieve beschrijvingen van de verdeling van numerieke variabelen

Om de vorm van de verdeling van een numerieke variabele te omschrijven worden vaak bepaalde woorden gebruikt. Het is handig als je die kent.

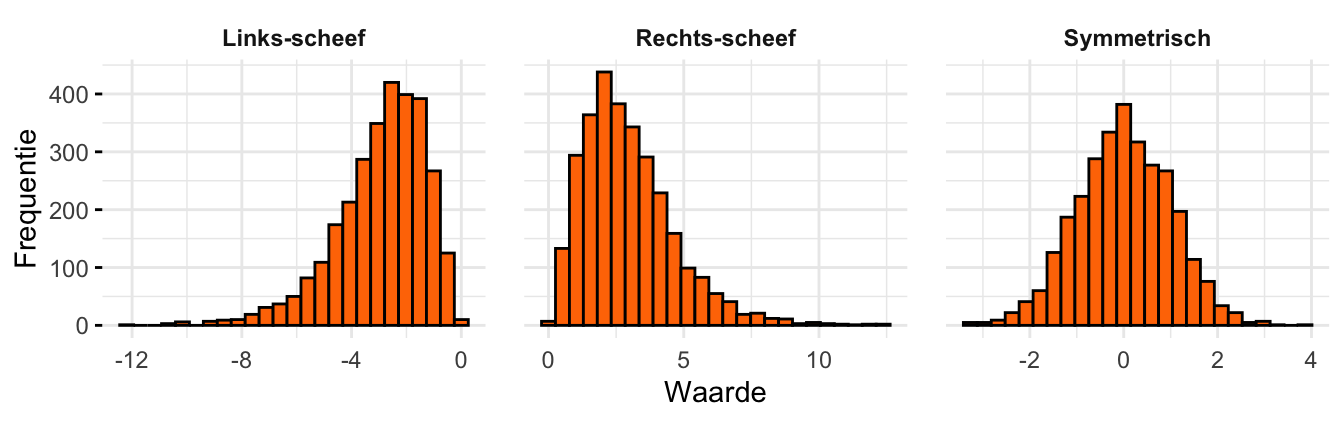
Een verdeling is symmetrisch als de vorm van het histogram (grofweg) spiegelsymmetrisch is. Als dat niet zo is, dan is de verdeling scheef (skewed). Het woord scheef wordt vooral gebruikt als de verdeling een “staart” heeft naar links of naar rechts. Heeft de verdeling een staart aan de linkerkant, dan is hij links-scheef (left-skewed); zit de staart aan de rechterkant, dan is hij rechts-scheef (right-skewed). Figuur 20.3 laat voorbeelden zien.

# Controleer of ggplot2 geladen is
if (!("ggplot2" %in% .packages())) { 
  library(ggplot2) 
}

# Stel een seed in voor reproduceerbaarheid
set.seed(123)

# Definieer parameters
aantal_punten <- 3 * 10^3  # Aantal punten per histogram
aantal_bins <- 25          # Aantal bins voor de histogrammen

# Genereer steekproeven uit gamma- en normale verdelingen
data <- data.frame(
  x = c(
    -rgamma(aantal_punten, shape = 3, scale = 1),  # Links-scheef
    rnorm(aantal_punten),                          # Symmetrisch
    rgamma(aantal_punten, shape = 3, scale = 1)    # Rechts-scheef
  ),
  groep = factor(
    rep(
      c("Links-scheef", "Symmetrisch", "Rechts-scheef"), 
      each = aantal_punten
    )
  )
)

# Plot de histogrammen per verdelingstype
ggplot(data, aes(x = x)) +
  geom_histogram(
    bins = aantal_bins, 
    fill = opvulkleur, 
    color = "black"
    ) +
  facet_wrap(~groep, nrow = 1, scales = "free_x") + 
  labs(
    x = "Waarde", 
    y = "Frequentie"
  ) +
  theme_minimal() +
  theme(
    strip.text = element_text(face = "bold"),  
    axis.text.y = element_text(size = 9),      
    axis.ticks.y = element_line(),             
    panel.spacing = unit(1, "lines")           
  )

Figuur 20.3: Illustraties van scheve en symmetrische verdelingen.

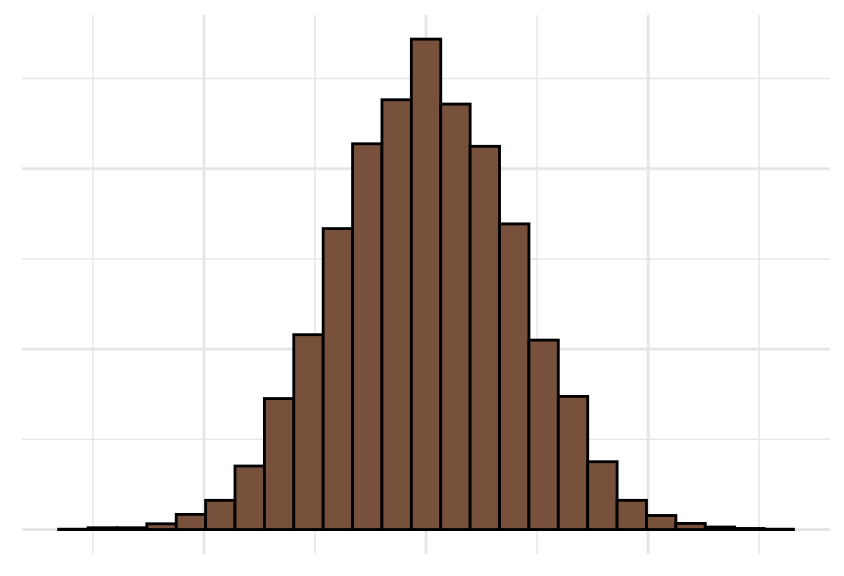
Verdelingen binnen de biologie en daarbuiten hebben vaak de vorm van een kerkklok (Figuur 20.4). We noemen ze dan klokvormig (bell shaped). Klokvormige verdelingen spelen later in de cursus een grote rol.

# kies een random seed om de figuur reproduceerbaar te maken
set.seed(125)

samplesize <- 10^4 # aantal punten per histogram
nr.bins <- 25

# genereer steekproef
data_klok <- rnorm(samplesize)

# histogram
ggplot(data.frame(x = data_klok), aes(x)) +
  geom_histogram(bins = nr.bins, fill = "#8c644e", color = "black") +
  theme_minimal() +
  theme(axis.ticks = element_blank(),
        axis.text = element_blank(),
        axis.title = element_blank()
        )

(a) Kerkklok (gemaakt met DALL·E 3)

(b) Klokvormige verdeling.

Figuur 20.4: Veel verdelingen in de biologie hebben een klokvorm.

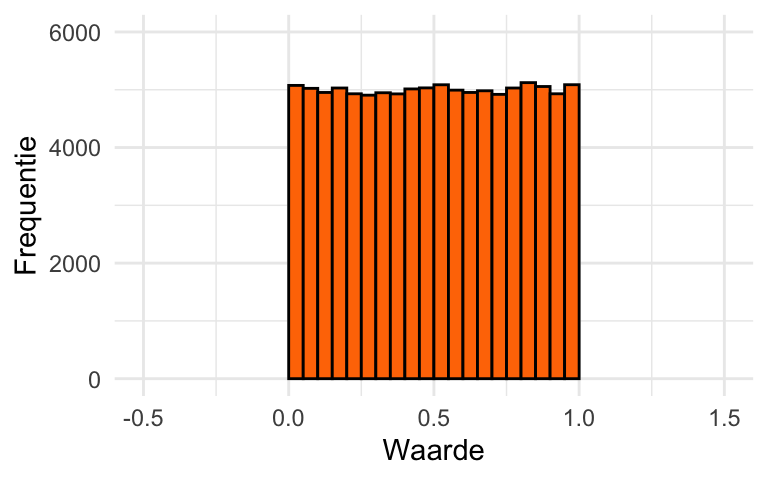
Een verdeling wordt uniform genoemd als iedere uitkomst even vaak voorkomt. Bijvoorbeeld, de verdeling in Figuur 20.5 heeft alleen waarden in het domein van 0 tot 1, en daar komen alle waarden ongeveer even vaak voor. Deze verdeling is dus ongeveer uniform in het domein tussen 0 en 1.

# Laad benodigde bibliotheken
if (!("ggplot2" %in% loadedNamespaces())) { library(ggplot2) }

# Stel een seed in voor reproduceerbaarheid
set.seed(125)

samplesize <- 10^5  # Aantal punten per histogram

# Genereer steekproef
data_unif <- runif(samplesize)  # Uniforme verdeling

# Histogram plotten
ggplot(data.frame(x = data_unif), aes(x)) +
  geom_histogram(
    binwidth = 0.05, boundary = 0, fill = opvulkleur, color = "black"
  ) +
  labs(
    title = NULL, # Titel
    x = "Waarde",      # Label voor de x-as
    y = "Frequentie"   # Label voor de y-as
  ) +
  theme_minimal() +
  coord_cartesian(
    xlim = c(-0.5, 1.5),
    ylim = c(0, 6000)
  )

Figuur 20.5: Histogram van een ongeveer uniforme verdeling.

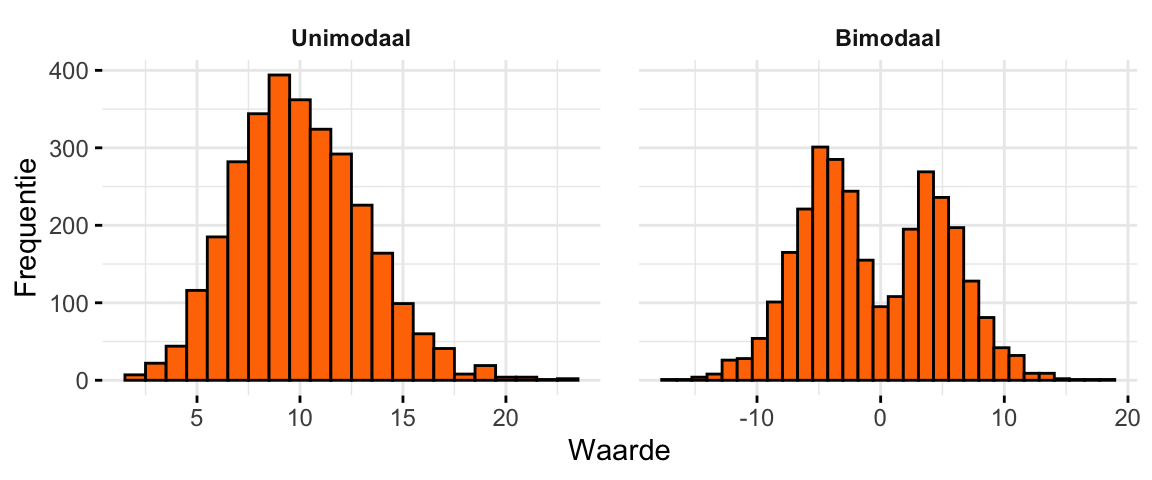
Een verdeling die één piek heeft noemen we unimodaal. Een verdeling met twee pieken is bimodaal (zie Figuur 20.6). Voor verdelingen met nog meer pieken bestaan ook namen (trimodaal, quadrimodaal, pentamodaal, …), maar die worden in de praktijk zelden gebruikt. Wel kom je soms multimodaal tegen voor verdelingen met meerdere pieken.

# Controleer of ggplot2 geladen is
if (!("ggplot2" %in% loadedNamespaces())) { 
  library(ggplot2) 
}

# Stel een seed in voor reproduceerbaarheid
set.seed(123)

# Definieer parameters
aantal_punten <- 3 * 10^3  # Aantal punten per histogram
aantal_bins <- 30          # Aantal bins voor de histogrammen

# Genereer steekproeven van twee gamma-verdelingen
data_links_scheef <- -rgamma(
  round(aantal_punten * 0.55), 
  shape = 8, scale = 1
  ) + 3
data_rechts_scheef <- rgamma(
  round(aantal_punten * 0.45), 
  shape = 8, scale = 1
  ) - 3

# Combineer om een bimodale verdeling te maken
data_bimodaal <- c(data_links_scheef, data_rechts_scheef)

# Genereer een unimodale verdeling (Poisson)
data_unimodaal <- rpois(aantal_punten, lambda = 10)

# Combineer gegevens en voeg een groepsvariabele toe
data <- data.frame(
  x = c(data_unimodaal, data_bimodaal),
  groep = factor(
    rep(
      c("Unimodaal", "Bimodaal"), 
      each = aantal_punten
    ), 
    levels = c("Unimodaal", "Bimodaal")
  )
)

# Plot de histogrammen per verdelingstype
ggplot(data, aes(x = x)) +
  geom_histogram(
    data = subset(data, groep == "Unimodaal"),
    binwidth = 1, 
    fill = opvulkleur, 
    color = "black"
  ) +
  geom_histogram(
    data = subset(data, groep == "Bimodaal"),
    bins = aantal_bins, 
    fill = opvulkleur, 
    color = "black"
  ) +
  facet_wrap(~groep, nrow = 1, scales = "free_x") +  
  labs(
    x = "Waarde",  
    y = "Frequentie"
  ) +
  theme_minimal() +
  theme(
    strip.text = element_text(face = "bold"),  
    axis.text.y = element_text(size = 9),      
    axis.ticks.y = element_line(),             
    axis.text.x = element_text(size = 9),      
    axis.ticks.x = element_line(),             
    panel.spacing = unit(1, "lines")           
  )

Figuur 20.6: Unimodale en bimodale verdelingen.

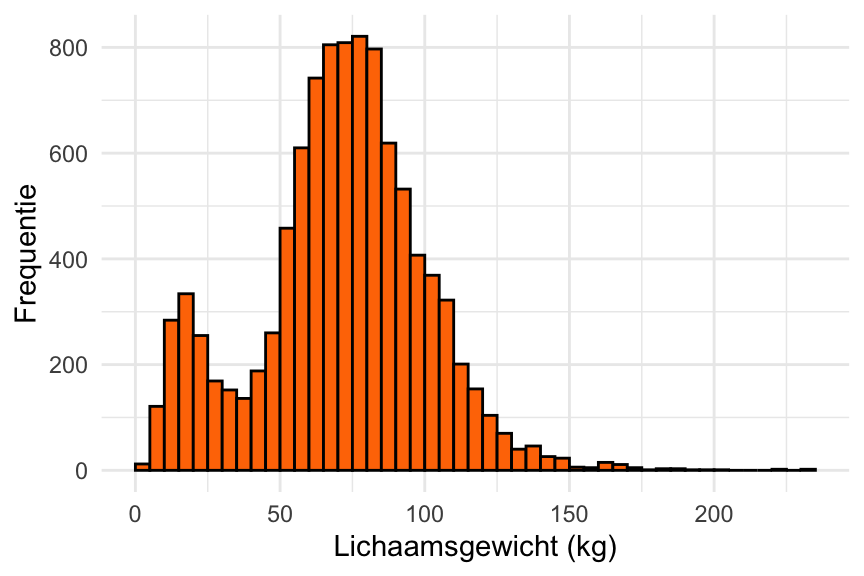
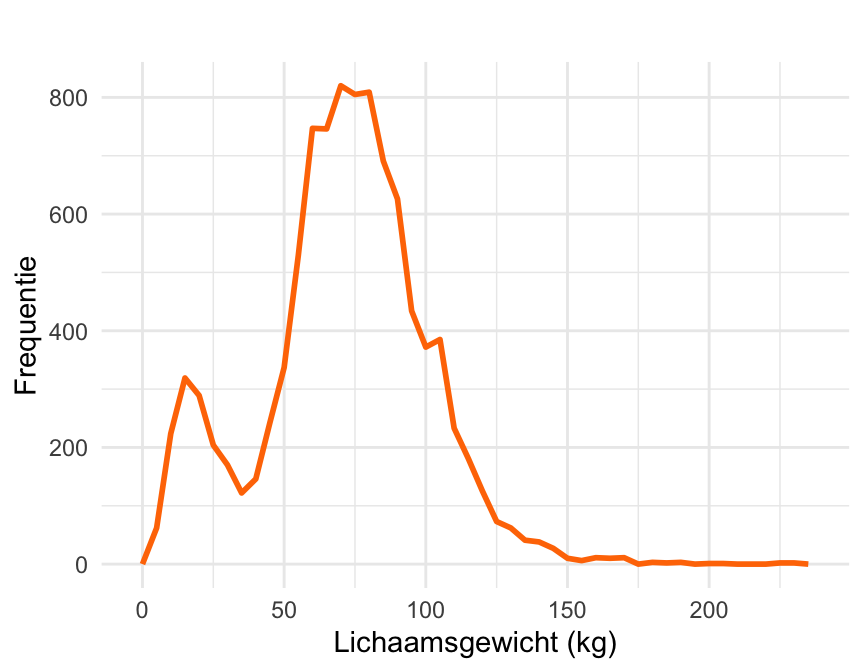
Multimodale verdelingen ontstaan vaak als binnen een steekproef meerdere deelpopulaties voorkomen met ieder een verschillend gemiddelde. De variabele Weight (lichaamsgewicht) uit de dataset NHANES is een voorbeeld.

Voorbeeld 20.1 (De verdeling van Weight is bimodaal in de dataset NHANES) De verdeling van Weight (lichaamsgewicht) in de dataset NHANES ziet er als volgt uit:

ggplot(
  data = NHANES, 
  aes(x = Weight)
  ) +
  geom_histogram(
    fill = opvulkleur, 
    color = "black", 
    binwidth = 5,
    boundary = 0,
    closed = "left"
    ) +
  labs(title = NULL,
    x = "Lichaamsgewicht (kg)",
    y = "Frequentie"
  ) +
  theme_minimal()

Figuur 20.7: Histogram van de lichaamsgewichten uit de NHANES-dataset.

Het histogram laat twee pieken zien: één rond 20 kg, en één in de buurt van 75 kg. De verdeling is dus bimodaal. In Oefening 20.17 zul je zelf aantonen waar die twee pieken vandaan komen.

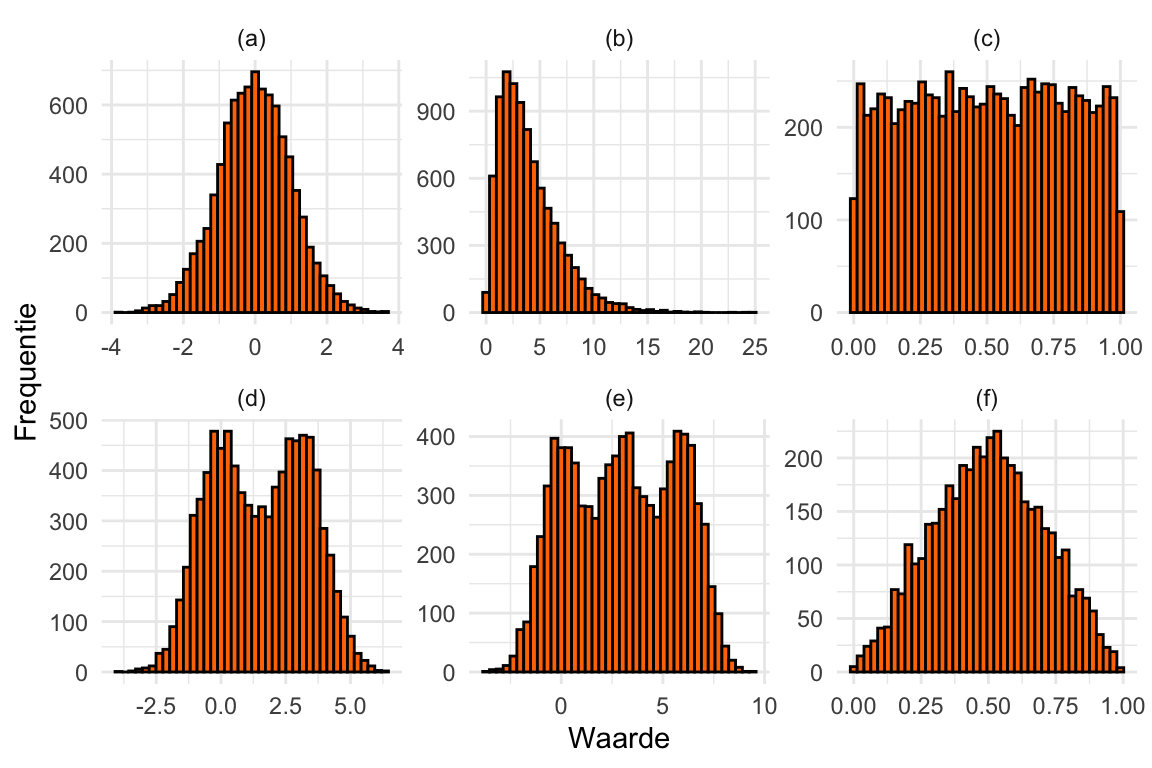
Oefening 20.3 (Omschrijf de verdeling)

library(ggplot2)

# Aantal samples
n <- 9000

# Data genereren
set.seed(124)

driehoek <- {x <- runif(n); x[runif(n) < pmax(0, abs(2 * (x - 0.5)))] <- NA; na.omit(x)}

data <- data.frame(
  value = c(
    rnorm(n),
    rgamma(n, shape = 2, scale = 2),
    runif(n),
    c(rnorm(n/2), rnorm(n/2, mean = 3)),
    c(rnorm(n/3), rnorm(n/3, mean = 3), rnorm(n/3, mean = 6)),
    driehoek
  ),
  distribution = c(
    rep(c("Normaal", 
          "Gamma (shape=2)", 
          "Uniform", 
          "Bimodaal", 
          "Trimodaal"), 
        each = n), 
    rep("Driehoek", 
        length(driehoek))),
  label = c(
    rep(c("(a)", 
          "(b)", 
          "(c)", 
          "(d)", 
          "(e)"), 
        each = n), 
    rep("(f)", 
        length(driehoek)))
)

# Plot maken
ggplot(data, aes(x = value, fill = distribution)) +
  geom_histogram(bins = 40, color = "black", alpha = 1, fill= opvulkleur) +
  facet_wrap(~label, scales = "free") +
  theme_minimal() +
  theme(legend.position = "none") +
  labs(x = "Waarde", y = "Frequentie")

Figuur 20.8: Welke termen zijn van toepassing op deze verdelingen?

Bekijk Figuur 20.8. Zet vervolgens in onderstaande tabel vinkjes waar de omschrijving van toepassing is.

	a.	b.	c.	d.	e.	f.
Symmetrisch
Links-scheef
Rechts-scheef
Klokvormig
Uniform
Bimodaal

20.5 De cumulatieve verdeling van een variabele

De cumulatieve verdeling (cumulative distribution) van een variabele laat zien welke fractie van de waarnemingen kleiner of gelijk is aan een bepaalde waarde. We leggen dit uit aan de hand van een voorbeeld.

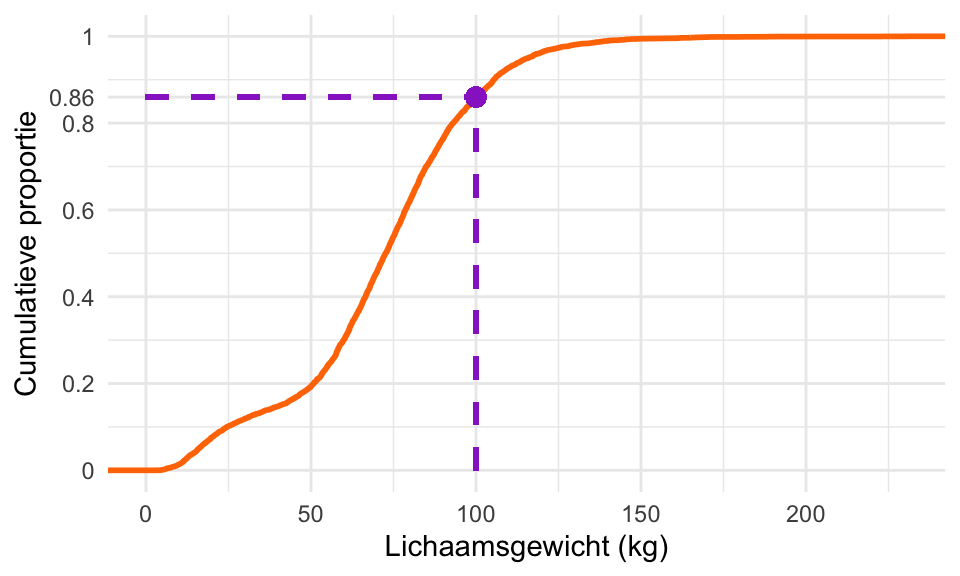
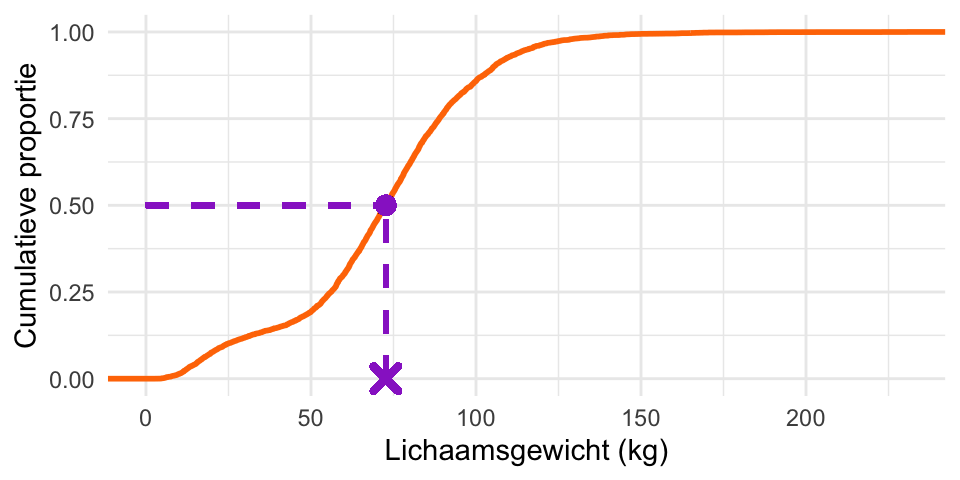
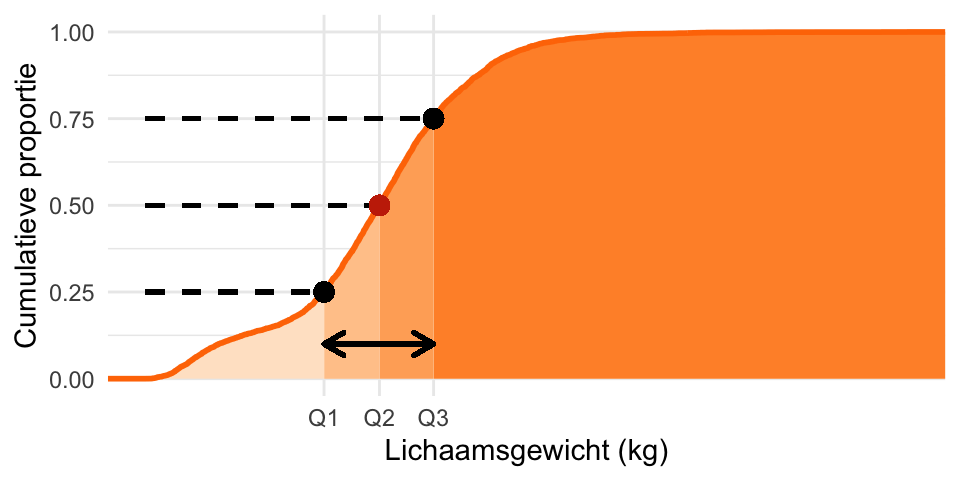
Voorbeeld 20.2 (De cumulatieve verdeling van lichaamsgewicht) In Figuur 20.9 is de cumulatieve verdeling van Weight (lichaamsgewicht) weergegeven (de oranje curve). Voor elk lichaamsgewicht op de \(x\)-as geeft curve aan welke proportie (deel, fractie) van de waarnemingen kleiner of gelijk is aan die waarde; dat wordt de cumulatieve proportie genoemd. De grafiek van de cumulatieve verdeling wordt de cumulatieve frequentiepolygoon genoemd.

Je kunt uit deze grafiek bijvoorbeeld aflezen (zie de paarse onderbroken lijnen) dat 86% van de mensen een gewicht heeft van hoogstens 100kg. De overige 14% weegt dus méér dan 100 kg.

# Maak een cumulatieve verdelingsplot
cumulplot <- ggplot(NHANES, aes(x = Weight)) +
  stat_ecdf(
    geom = "step", 
    color = opvulkleur, 
    size = 1, 
    bw = 2
  ) +
  labs(
    x = "Lichaamsgewicht (kg)",
    y = "Cumulatieve proportie"
  ) + 
  theme_minimal()

# Definieer het kruispunt van de lijnen
kruispunt <- c(100, 0.86)

cumulplot +
  # Voeg een horizontale stippellijn toe bij 0.86
  geom_segment(
    aes(
      x = 0, xend = kruispunt[1], 
      y = kruispunt[2], yend = kruispunt[2]
    ), 
    linetype = "dashed", 
    color = lijnkleur1, 
    size = 1
  ) +
  # Voeg een verticale stippellijn toe bij 100 kg
  geom_segment(
    aes(
      x = kruispunt[1], xend = kruispunt[1], 
      y = 0, yend = kruispunt[2]
    ), 
    linetype = "dashed", 
    color = lijnkleur1, 
    size = 1
  ) +
  # Voeg een punt toe op het kruispunt van de lijnen
  geom_point(
    aes(x = kruispunt[1], y = kruispunt[2]), 
    color = lijnkleur1, 
    size = 3
  ) +
  scale_y_continuous(
    breaks = c(0, 0.2, 0.4, 0.6, 0.8, 0.86, 1),  
    minor_breaks = c(0.1, 0.3, 0.5, 0.7, 0.9),  
    labels = function(breaks) ifelse(breaks == 0.86, "0.86", breaks)
  )

Figuur 20.9: Cumulatieve verdeling van lichaamsgewicht in de NHANES-dataset. De paarse onderbroken lijnen laten zien dat 86% van de mensen in de dataset hoogstens 100kg weegt.

De cumulatieve verdeling is altijd een stijgende functie die loopt van 0 (bij de kleinste waarde binnen de waarnemingen) tot 1 (bij de grootste waarde).

Oefening 20.4 (De cumulatieve verdeling)

Gebruik Figuur 20.9 om de antwoorden te schatten op de volgende vragen.

1. Welk percentage van de mensen weegt hoogstens 75kg?
2. Welk percentage van de mensen weegt meer dan 50kg?
3. Welk percentage van de mensen heeft een gewicht tussen 75 en 100kg?
4. Stel, we selecteren de lichtste 10% van deze populatie. Hoeveel weegt de zwaarste persoon in deze groep?

20.6 Ligging en spreiding van een verdeling

Om de verdeling van een variabele te karakteriseren kunnen we naast woorden ook getallen gebruiken. Dat soort getallen worden kengetallen of statistieken genoemd.

Om de verdeling van een numerieke variabele kort te omschrijven geven we vaak twee getallen. De eerste waarde geeft de ligging (location) aan van de verdeling. Daarmee geven we de plek aan op de \(x\)-as waar de waarden van de variabele zich (ongeveer) bevinden. We kunnen de ligging aangeven door een typische waarde voor de variabele te bepalen.

Het tweede getal geeft de spreiding (spread) van de verdeling weer. De spreiding drukt uit in hoeverre de verschillende waarden van elkaar verschillen; dus in hoeverre ze verspreid zijn.

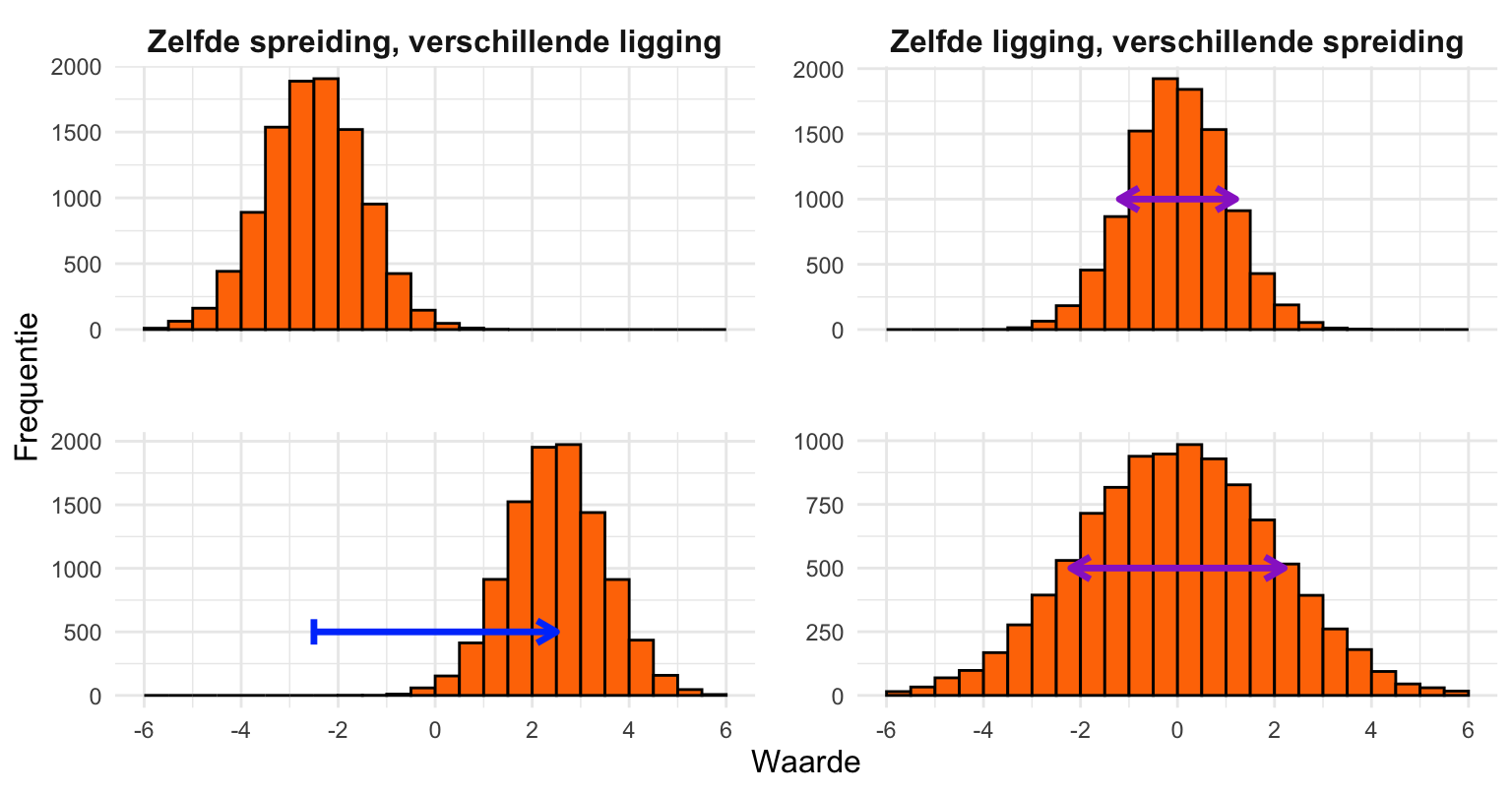
Figuur 20.10 illustreert de begrippen ligging en spreiding aan de hand van histogrammen. De twee histogrammen aan de linkerkant zijn enkel ten opzichte van elkaar verschoven. Daarom verschilt hun ligging maar is hun spreiding gelijk. De twee histogrammen aan de rechterkant liggen ongeveer op dezelfde plek, gecentreerd op de waarde 0, maar in het onderste histogram zijn de waarden over een groter domein verspreid. (De piek is breder.) Daarom verschilt hun spreiding, maar is hun ligging gelijk.

# Laad benodigde bibliotheken
if (!("ggplot2" %in% loadedNamespaces())) { library(ggplot2) }

# Stel een seed in voor reproduceerbaarheid
set.seed(124)

# Parameters
steekproefgrootte <- 10^4  # Aantal punten per histogram
gemiddelde1 <- 0           # Gemiddelde voor de eerste verdeling
gemiddelde2 <- gemiddelde1 + 1.5  # Gemiddelde voor de verschoven verdeling
standaardafwijking1 <- 1   # Standaardafwijking voor de eerste verdeling
standaardafwijking2 <- standaardafwijking1 * 2  # Verdubbelde standaardafwijking

# Data genereren
data <- data.frame(
  waarden = c(
    rnorm(steekproefgrootte, gemiddelde1 - 2.5, standaardafwijking1),  # Linksboven: verschoven naar links
    rnorm(steekproefgrootte, gemiddelde1, standaardafwijking1),        # Rechtsboven
    rnorm(steekproefgrootte, gemiddelde2 + 1, standaardafwijking1),    # Linksonder: verschoven naar rechts
    rnorm(steekproefgrootte, gemiddelde1, standaardafwijking2)         # Rechtsonder: grotere spreiding
  ),
  groep = factor(
    rep(
      c(
        "Zelfde spreiding, verschillende ligging", 
        "Zelfde ligging, verschillende spreiding",
        "Linksonder", 
        "Rechtsonder"
      ), 
      each = steekproefgrootte
    ),
    levels = c(
      "Zelfde spreiding, verschillende ligging", 
      "Zelfde ligging, verschillende spreiding", 
      "Linksonder", 
      "Rechtsonder"
    )
  )
)

# Paneltitels aanpassen
paneel_titels <- data.frame(
  groep = factor(
    c(
      "Zelfde spreiding, verschillende ligging", 
      "Zelfde ligging, verschillende spreiding", 
      "Linksonder", 
      "Rechtsonder"
    ),
    levels = levels(data$groep)
  ),
  titel = c(
    "Zelfde spreiding, verschillende ligging", 
    "Zelfde ligging, verschillende spreiding", 
    "", 
    ""
  )
)

annotatie_linksonder <- data.frame(
  x = c(gemiddelde1 - 2.5),
  xend = c(gemiddelde2 + 1),
  y = c(500),
  yend = c(500),
  groep = "Linksonder"
)

annotatie_rechtsboven <- data.frame(
  x = c(gemiddelde1 - 1.2 * standaardafwijking1),
  xend = c(gemiddelde1 + 1.2 * standaardafwijking1),
  y = c(1000),
  yend = c(1000),
  groep = "Zelfde ligging, verschillende spreiding"
)

annotatie_rechtsonder <- data.frame(
  x = c(gemiddelde1 - 1.1 * standaardafwijking2),
  xend = c(gemiddelde1 + 1.1 * standaardafwijking2),
  y = c(500),
  yend = c(500),
  groep = "Rechtsonder"
)

# plot
basis_plot <- ggplot(data, aes(x = waarden)) +
  geom_histogram(
    binwidth = 0.5, 
    boundary = 0,
    fill = opvulkleur, 
    color = "black"
  ) +
  geom_segment(
    data = annotatie_linksonder,
    aes(x = x, xend = xend, y = y, yend = yend),
    arrow = arrow(length = unit(0.3, "cm")), 
    color = lijnkleur3,  
    size = 1.2
  ) +
  geom_segment(
    data = annotatie_linksonder,
    aes(x = x, xend = x, y = y - 100, yend = yend + 100),
    color = lijnkleur3,  
    size = 1.2
  ) +
  geom_segment(
    data = annotatie_rechtsboven,
    aes(x = x, xend = xend, y = y, yend = yend),
    arrow = arrow(ends = "both", length = unit(0.3, "cm")), 
    color = lijnkleur1, 
    size = 1.2
  ) +
  geom_segment(
    data = annotatie_rechtsonder,
    aes(x = x, xend = xend, y = y, yend = yend),
    arrow = arrow(ends = "both", length = unit(0.3, "cm")),
    color = lijnkleur1, 
    size = 1.2
  ) +
  facet_wrap(
    ~factor(
      groep, c(
        "Zelfde spreiding, verschillende ligging", 
        "Zelfde ligging, verschillende spreiding",
        "Linksonder", 
        "Rechtsonder"
      )
    ), 
    ncol = 2, 
    scales = "free_y", 
    labeller = as_labeller(setNames(paneel_titels$titel, paneel_titels$groep))
  ) +
  scale_x_continuous(
    limits = c(-6, 6), 
    breaks = seq(-6, 6, by = 2)
  ) +  # Gelijke x-assen
  labs(
    x = "Waarde",
    y = "Frequentie"
  ) +
  theme_minimal() +
  theme(
    strip.text = element_text(face = "bold", size = 12),  # Paneltitels
    panel.spacing = unit(1, "lines"),                    # Ruimte tussen panelen
    axis.title.x = element_text(size = 12),
    axis.title.y = element_text(size = 12)
  )

basis_plot

Figuur 20.10: Illustratie van de begrippen ligging en spreiding.

20.7 Maten voor de ligging van een verdeling

Om de ligging en spreiding van een verdeling in getallen uit te drukken worden verschillende maten gebruikt.

Maten voor de ligging worden ook wel centrummaten genoemd (measures of central tendency). Hieronder bespreken we drie verschillende centrummaten: de modus, de mediaan, en het gemiddelde (mean). Deze drie maten geven allemaal een “typische” waarde voor de variabele, maar “typisch” is bij iedere maat net anders gedefinieerd.

De modus

Met de modus wordt de waarde bedoeld die het vaakst voorkomt. Bij categorische variabelen kun je simpelweg tellen welke uitkomst dat is. Bij numerieke variabelen wordt meestal het interval bedoeld dat hoort bij de hoogste staaf van het histogram. Als er meerdere pieken zijn, dan zijn er meerdere modi (meervoud van modus). Daar komen ook de woorden unimodaal, bimodaal, etc. vandaan. In Figuur 20.7, het histogram van Weight, waren twee pieken te zien. Er zijn dan ook twee modi: het interval \([15,20)\) en het interval \([75,80)\).

De mediaan

De mediaan van een serie waarnemingen is een getal met de eigenschap dat de helft van de waarnemingen kleiner is en de helft van de waarnemingen groter. De berekening gaat als volgt:

• Sorteer de waarnemingen van klein naar groot.
• Als het aantal waarnemingen \(n\) oneven is, dan is de mediaan het middelste getal in de gesorteerde rij.
• Als het aantal waarnemingen \(n\) even is, dan bestaat zo’n middelste getal niet; in dat geval nemen we het gemiddelde van de middelste twee getallen.

In dit boek noteren we de mediaan van een serie waarnemingen \(x_1\), \(x_2\), \(\ldots, x_n\) als \(\tilde{x}\).

Voorbeeld 20.3 (De mediaan van je tentamencijfers) Laten we een voorbeeld nemen. Stel dat je voor vijf tentamens de volgende cijfers hebt gehaald:

\[7 \qquad 7{,}5 \qquad 1 \qquad 8{,}5 \qquad 9.\] Wat is dan de mediaan van je cijfers? We sorteren de cijfers en krijgen

\[1 \qquad 7 \qquad {\color{darkorange}7{,}5} \qquad 8{,}5 \qquad 9.\]

Het getal midden in de rij is de \({\color{darkorange}7{,}5}\) en dus is de mediaan \(\tilde{x} = {\color{darkorange}7{,}5}\).

Als je voor het volgende tentamen een 10 haalt, verandert de gesorteerde reeks als volgt:

\[1 \qquad 7 \qquad {\color{darkorange}7{,}5} \qquad {\color{darkorange}8{,}5} \qquad 9 \qquad 10.\]

Omdat het aantal tentamencijfers nu even is, is er geen middelste getal meer. Als mediaan nemen we daarom het gemiddelde van de twee middelste getallen:

\[\tilde{x}=\frac{{\color{darkorange}7{,}5} + {\color{darkorange}8{,}5}}{2} = 8.\]

De mediaan is een typische of representatieve waarde in de zin dat er evenveel waarden groter zijn als kleiner.

In Paragraaf 20.5 hebben we de cumulatieve verdeling besproken. Omdat de helft van de waarnemingen kleiner is dan de mediaan is de cumulatieve proportie die hoort bij de mediaan gelijk aan \(0{,}5\). Je kunt de mediaan daarom uit de cumulatieve verdeling aflezen door de waarde op de \(x\)-as te bepalen die hoort bij een cumulatieve proportie van \(0{,}5\). Figuur 20.11 laat dat zien voor de variabele Weight in de NHANES-dataset.

# Bereken de kwartielen van de Weight-variabele
quantiles <- quantile(
  NHANES$Weight, 
  probs = c(0.25, 0.5, 0.75), 
  na.rm = TRUE
)

# Voeg lijnen, punten en labels toe aan de cumulatieve plot
cumulplot_median <- cumulplot +
  # Horizontale lijn bij de mediaan
  geom_segment(
    aes(
      x = 0, xend = quantiles[2], 
      y = 0.5, yend = 0.5
    ),
    linetype = "dashed", 
    color = lijnkleur1, 
    size = 1
  ) +
  # Verticale lijn bij de mediaan
  geom_segment(
    aes(
      x = quantiles[2], xend = quantiles[2], 
      y = 0, yend = 0.5
    ),
    linetype = "dashed", 
    color = lijnkleur1, 
    size = 1
  ) +
  # Punt op het kruispunt van mediaan en cumulatieve proportie 0.5
  geom_point(
    aes(
      x = quantiles[2], 
      y = 0.5
    ),
    color = lijnkleur1, 
    size = 3
  ) +
  # Kruis op de x-as bij de mediaan
  geom_point(
    aes(
      x = quantiles[2], 
      y = 0
    ),
    color = "black", 
    shape = 4, 
    size = 2, 
    stroke = 2
  ) +
  # Labels voor titel en assen
  labs(
    title = NULL,
    x = "Lichaamsgewicht (kg)",
    y = "Cumulatieve proportie"
  )

# Toon de plot met de mediaan
cumulplot_median

Figuur 20.11: Cumulatieve verdeling van lichaamsgewicht in de NHANES-dataset. De mediaan is met een kruis op de \(x\)-as aangegeven. Per definitie is de helft van de waarnemingen kleiner dan de mediaan. Daarom bereikt de cumulatieve verdeling op dat punt precies een half.

Het gemiddelde

De meest gebruikte maat voor de ligging van een verdeling is het gemiddelde. Zoals je weet, is het gemiddelde de optelsom van alle waarden, gedeeld door het aantal waarden.

Om de definitie van het gemiddelde wiskundig te kunnen noteren, moeten we wat afspraken maken. Het aantal waarnemingen noemen we \(n\). Iedere individuele waarneming geven we een nummer van 1 tot \(n\); zo’n nummer wordt een index genoemd. De waarde van de waarneming met index 1 noteren we als \(x_1\), de waarde van de waarneming met index 2 als \(x_2\), enzovoort. Het gemiddelde \(\overline{x}\) van de waarnemingen kunnen we dan definiëren als: \[ \overline{x} = \frac{\sum_{i=1}^n x_i}{n}. \qquad(20.1)\] (Ken je het sommatieteken nog? Kijk anders terug naar Paragraaf 4.4.)

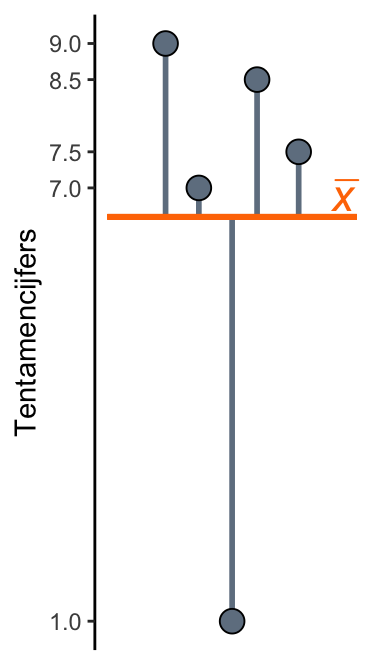
Het is nu nuttig om je het gemiddelde voor te stellen als het zwaartepunt van de waarden. Om dat concreet te maken stellen we ons weer voor dat je voor vijf tentamens de volgende cijfers hebt gehaald:

\[7 \qquad 7{,}5 \qquad 1 \qquad 8{,}5 \qquad 9.\]

Stel je die cijfers voor als kralen die op een getallenlijn geprikt zijn, zoals in Figuur 20.12 hieronder. Als je de getallenlijn precies bij het gemiddelde op het oranje driehoekje plaatst, dan blijft het geheel in balans. (We gaan er vanuit dat de getallenlijn zelf niets weegt.)

# Plot de volgende getallen
x <- c(1, 7, 7.5, 8.5, 9)
m <- mean(x)

# Genereer een data frame met zowel de getallen als hun labels
df <- data.frame(x = x, label = as.character(x))

# Teken de figuur
ggplot(df, aes(x = x, y = 0)) +
  geom_segment( # dunne as, "gewichtsloos"
    aes(x = min(x), xend = max(x), y = 0, yend = 0),
    size = 1, 
    color = "SlateGray"
    ) +
  geom_point( # plot de getallen als gevulde cirkels
    shape = 21, size = 6, fill = "SlateGray"
    ) + 
  geom_text( # geef ze labels
    aes(label = label), vjust = -1, size = 5
    ) +   
  annotate( # teken een driehoek onder het zwaartepunt / gemiddelde
    "polygon", 
    x = c(m, m - 0.2, m + 0.2),
    y = c(0, -0.3, -0.3), 
    fill = opvulkleur
    ) + 
  coord_cartesian(xlim = c(min(x), max(x)), ylim = c(-0.6, 0.5)) +
  annotate(
    "text", 
    x = m, 
    y = 0.2, 
    label = expression(
      bar(italic(x))), 
      size = 7, 
    vjust = 1, 
    color = opvulkleur
    ) +
  theme_void() + # geen y-as, geen ticks, geen labels
  theme(axis.line.x = element_blank())

Figuur 20.12: Het gemiddelde als het zwaartepunt van de getallen

Merk trouwens op dat alle tentamencijfers voldoende zijn, behalve één trieste uitzondering: een 1. Zo’n waarneming die ver buiten de rest van de reeks ligt noemen we een uitbijter (outlier). Uitbijters kunnen een groot effect hebben op het gemiddelde. Dat zie je ook in Figuur 20.12: doordat de 1 zo ver van de andere cijfers ligt, kan deze in z’n eentje als tegenwicht dienen voor alle andere getallen. Het is de moeite waard om deze toets te herkansen.

Oefening 20.5 (Gevoeligheid voor uitbijters)

Je tentamencijfers zijn zoals weergegeven in Figuur 20.12. Stel dat je het tentamen waarvoor je een 1 had gehaald mag herkansen. Je haalt voor het hertentamen een 7.

1. Wat is het effect op je gemiddelde cijfer?

2. Wat is het effect op de mediaan?

3. Welke waarde is gevoeliger voor uitbijters?

Een andere nuttige manier om naar het gemiddelde te kijken is Figuur 20.13 hieronder. Dezelfde tentamencijfers zijn nu op de verticale as geplot. (De horizontale positie van de punten is willekeurig.) De oranje lijn markeert het gemiddelde \(\overline{x}\). Vanuit ieder punt is een verticale grijze lijn getekend die het verschil aangeeft tussen de waarneming en het gemiddelde. Dat verschil wordt het residu (residual) genoemd.

# Maak een dataset met handmatige jitter
data <- data.frame(
  x = c(0, -0.04, 0.08, 0.03, -0.08), # handmatige jitter
  y = x
)

ggplot(data, aes(x = x, y = y)) +
  # Verticale lijnen naar het gemiddelde
  geom_segment(
    aes(
      x = x, xend = x, 
      y = y, yend = m
    ),
    color = "SlateGray",
    linetype = "solid",
    size = 1
  ) +
  # Punten
  geom_point(
    shape = 21, 
    fill = "SlateGray", 
    size = 4
  ) +
  # Gemiddelde lijn
  geom_segment(
    aes(
      x = -0.15, xend = 0.15, 
      y = m, yend = m
    ),
    color = opvulkleur,
    size = 1
  ) +
  # Label bij de gemiddelde lijn
  annotate(
    "text",
    x = 0.12, 
    y = m + 0.3,
    label = expression(bar(italic(x))),
    color = opvulkleur,
    hjust = 0,
    size = 6
  ) +
  # Y-as instellen
  scale_y_continuous(
    breaks = x, 
    limits = c(min(x), max(x)),
    labels = scales::number_format(accuracy = 0.1)
  ) +
  ylab("Tentamencijfers") +
  # Geen x-as, geen gridlijnen
  theme_classic() +
  theme(
    axis.title.x = element_blank(),
    axis.text.x = element_blank(),
    axis.line.x = element_blank(),
    axis.ticks.x = element_blank(),
    panel.grid.major.x = element_blank(),
    panel.grid.minor.x = element_blank()
  )

Figuur 20.13: Elastiekjes trekken de oranje lijn precies naar het gemiddelde.

Intuïtief verwacht je misschien dat het gemiddelde de waarde is die zo dicht mogelijk bij alle punten ligt. Dat zou betekenen dat de oranje lijn precies op de hoogte ligt die de totale lengte van de grijze lijntjes zo kort mogelijk maakt. Dat is helaas niet het geval. Maar stel nu dat we de lengtes van de grijze lijntjes eerst kwadrateren voordat we ze optellen. Deze som van deze kwadraten noemen we de kwadratensom (sum of squares, \(\mathrm{SS}\)):

\[ \mathrm{SS} = \sum_{i=1}^n \left( x_i - \overline{x}\right)^2. \qquad(20.2)\]

Het gemiddelde \(\overline{x}\) is wél de waarde die deze kwadratensom minimaliseert. Voor wie benieuwd is: de afleiding kun je vinden in Bijlage A.

Je kunt je de grijze lijntjes voorstellen als elastiekjes die zowel aan de oranje lijn als aan de datapunten vastgeknoopt zijn. Alle datapunten trekken via hun elastiekje aan de oranje lijn, die daardoor omhoog of omlaag zal bewegen totdat de krachten in evenwicht zijn. De evenwichtspositie is precies het gemiddelde.

De trek-kracht van een elastiekje wordt groter als deze verder wordt uitgerekt. Punten die verder van de oranje lijn afliggen, trekken daardoor harder. De oranje lijn zal dus sterk naar uitbijters worden toegetrokken. Op die manier kun je dus weer inzien dat het gemiddelde gevoelig is voor uitbijters.

Waarom werkt de metafoor van de elastiekjes?

Het is geen toeval dat de metafoor van de elastiekjes werkt. De evenwichtspositie van de oranje lijn is de positie waar de totale potentiële energie minimaal is. Voor een “ideale” elastiek of veer geldt dat de potentiële energie gelijk is aan \(E(u) = \frac{1}{2} k u^2\), waarbij \(u\) de uitrekking is en \(k\) de veerconstante. De energie hangt dus samen met het kwadraat van de uitrekking, en de totale energie is minimaal op de positie waar de som van de kwadraten van \(u\) minimaal is. De oranje lijn komt dus inderdaad tot rust bij het gemiddelde.

20.8 Maten voor de spreiding van een verdeling

Na de centrummaten zijn nu de spreidingsmaten aan de beurt.

Het bereik

Het bereik (range) van een rij getallen is het interval dat begint bij het kleinste getal en eindigt met het grootste getal. Dus, het bereik van de vijf tentamencijfers uit Voorbeeld 20.3 is het interval \([1, 9]\).

Kwantielen en de interkwartielafstand

Om de mediaan te bepalen, deelde je de waarnemingen in twee groepen: de kleinere waarden en de grotere waarden (Paragraaf 20.7.2). De mediaan is de scheidslijn tussen deze twee groepen.

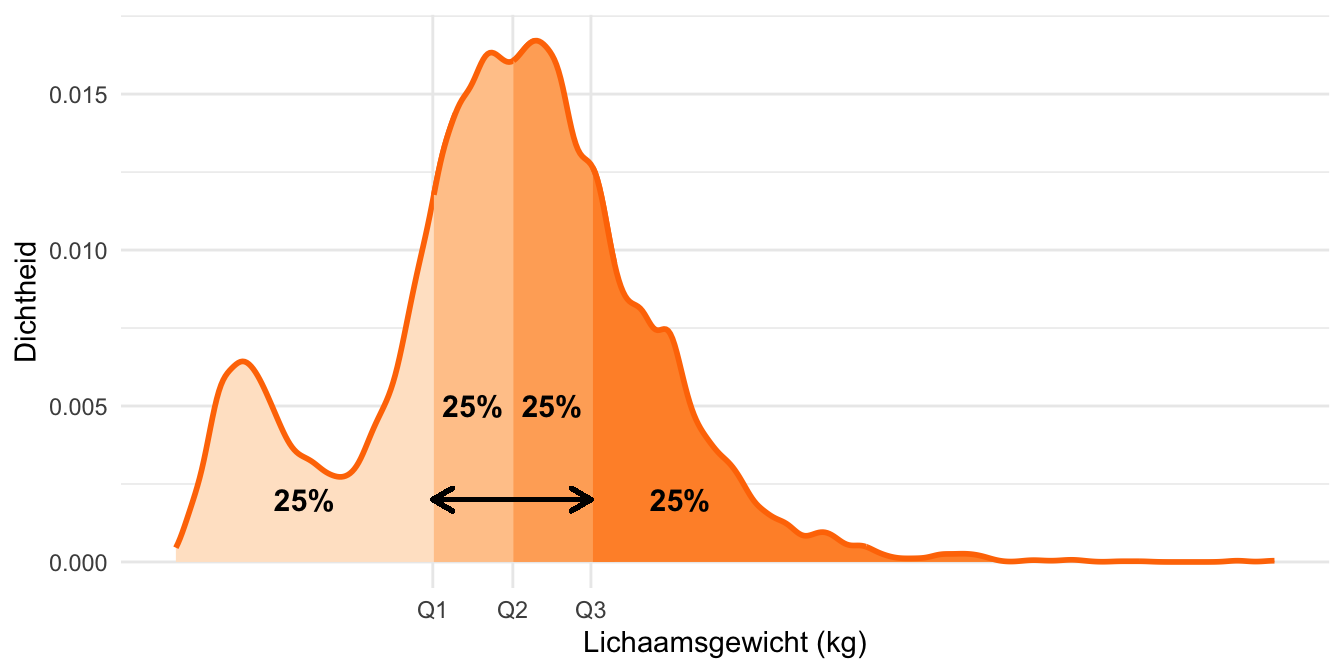
Om de kwartielen (quartiles) te definiëren splitsen we de twee helften nogmaals in tweeën, waardoor we vier kwarten krijgen. De kwartielen zijn de grenzen tussen deze vier delen. Een kwart van de waarnemingen is kleiner dan het eerste kwartiel (Q1). De helft van de waarnemingen is kleiner dan het tweede kwartiel (Q2); die is dus precies gelijk aan de mediaan. Drie kwart van de waarnemingen is kleiner dan het derde kwartiel (Q3). De kwartielen zijn in Figuur 20.14 geïllustreerd.

# Laad de benodigde bibliotheken als ze nog niet beschikbaar zijn
if (!("ggplot2" %in% .packages())) { library("ggplot2") }
if (!("NHANES" %in% .packages())) { library("NHANES") }
if (!("dplyr" %in% .packages())) { library("dplyr") }

# Gebruik de Weight-variabele uit de NHANES dataset
data <- NHANES %>%
  filter(!is.na(Weight)) %>%
  select(Weight)

# Bereken kwartielen
quartiles <- quantile(data$Weight, probs = c(0.25, 0.50, 0.75, 1.0))
q1 <- quartiles[1]  # Q1 (25e percentiel)
q2 <- quartiles[2]  # Q2 (50e percentiel / Mediaan)
q3 <- quartiles[3]  # Q3 (75e percentiel)
q4 <- quartiles[4]  # Q4 (100e percentiel)

# Functie om een kleur lichter te maken
lighten_color <- function(color, percentage) {
  # Zorg ervoor dat het percentage tussen 0 en 1 ligt
  percentage <- max(0, min(percentage, 1))
  
  # Converteer de kleur naar RGB en meng met wit
  rgb <- col2rgb(color) / 255
  blended_rgb <- rgb + (1 - rgb) * percentage
  
  # Retourneer de kleur in HEX-formaat
  rgb(blended_rgb[1], blended_rgb[2], blended_rgb[3], maxColorValue = 1)
}

# Maak een density-plot met kwartielgebaseerde opvulling
ggplot(data, aes(x = Weight)) +
  # Volledige density-plot (achtergrondlaag) met bw = 2
  geom_density(
    aes(
      y = ifelse(after_stat(x) <= q1 + 5, after_stat(density), NA)
    ),
    color = opvulkleur,
    fill = lighten_color(opvulkleur, 0.8),
    bw = 2,
    size = 1
  ) +
  # Density-plot voor Q1 tot Q2
  geom_density(
    aes(
      y = ifelse(
        after_stat(x) >= q1 & after_stat(x) <= q2 + 5,
        after_stat(density),
        NA
      )
    ),
    color = opvulkleur,
    fill = lighten_color(opvulkleur, 0.6),
    bw = 2,
    size = 1
  ) +
  # Density-plot voor Q2 tot Q3
  geom_density(
    aes(
      y = ifelse(
        after_stat(x) >= q2 & after_stat(x) <= q3 + 5,
        after_stat(density),
        NA
      )
    ),
    color = opvulkleur,
    fill = lighten_color(opvulkleur, 0.4),
    bw = 2,
    size = 1
  ) +
  # Density-plot voor Q3 tot Q4
  geom_density(
    aes(
      y = ifelse(after_stat(x) >= q3, after_stat(density), NA)
    ),
    color = opvulkleur,
    fill = lighten_color(opvulkleur, 0.2),
    bw = 2,
    size = 1
  ) +
  # Voeg aangepaste x-as ticks en labels toe voor de kwartielen
  scale_x_continuous(
    breaks = c(q1, q2, q3),
    labels = c("Q1", "Q2", "Q3"),
    minor_breaks = NULL
  ) +
  # Voeg "25%" labels toe aan elk deel
  annotate(
    "text",
    x = (min(data$Weight) + q1) / 2,
    y = 0.002,
    label = "25%",
    color = "black",
    size = 4,
    fontface = "bold"
  ) +
  annotate(
    "text",
    x = (q1 + q2) / 2,
    y = 0.005,
    label = "25%",
    color = "black",
    size = 4,
    fontface = "bold"
  ) +
  annotate(
    "text",
    x = (q2 + q3) / 2,
    y = 0.005,
    label = "25%",
    color = "black",
    size = 4,
    fontface = "bold"
  ) +
  annotate(
    "text",
    x = (q3 + 0.15 * q4) / 1.15,
    y = 0.002,
    label = "25%",
    color = "black",
    size = 4,
    fontface = "bold"
  ) +
  labs(
    title = NULL,
    x = "Lichaamsgewicht (kg)",
    y = "Dichtheid"
  ) +
  geom_segment(
    aes(
      x = quantiles[1],
      xend = quantiles[3],
      y = 0.002,
      yend = 0.002
    ),
    arrow = arrow(ends = "both", length = unit(0.3, "cm")),
    color = "black",
    size = 0.8,
    lineend = "round"
  ) +
  theme_minimal()

Figuur 20.14: Illustratie van de kwartielen. De plot laat de verdeling van Weight (lichaamsgewicht) zien uit de NHANES dataset. De kwartielen Q1, Q2 en Q3 zijn bij de x-as aangegeven. Op die manier wordt de plot in vier stukken verdeeld met ieder 25% van de waarnemingen.

De interkwartielafstand (IKA; interquartile range) wordt gedefinieerd als het verschil tussen Q3 en Q1:

\[ \mathrm{IKA} = \mathrm{Q3} - \mathrm{Q1} \qquad(20.3)\]

In Figuur 20.14 is de IKA weergegeven met een dubbele pijl die van Q1 naar Q3 loopt.

De IKA is een maat voor de spreiding van de gegevens omdat het aangeeft hoe breed het interval is waarin zich de “middelste” 50% van de waarnemingen bevindt.

Je kunt de kwartielen en de IKA ook bepalen met behulp van de cumulatieve verdelingsfunctie. In Figuur 20.15 snijden de horizontale zwarte lijnen de \(y\)-as bij \(0{,}25\) en \(0{,}75\), en raken de cumulatieve verdeling daarom precies bij Q1 en Q3. De zwarte pijl geeft weer de IKA aan.

# Laad de benodigde bibliotheken als ze nog niet geladen zijn
if (!("ggplot2" %in% loadedNamespaces())) { library(ggplot2) }
if (!("dplyr" %in% loadedNamespaces())) { library(dplyr) }
if (!("NHANES" %in% loadedNamespaces())) { library(NHANES) }
if (!("dplyr" %in% loadedNamespaces())) { library(dplyr) }

# Gebruik de Weight-variabele uit de NHANES dataset
data <- NHANES %>%
  filter(!is.na(Weight)) %>%
  select(Weight)

# Bereken kwartielen
quartiles <- quantile(data$Weight, probs = c(0.25, 0.50, 0.75, 1.0))
q1 <- quartiles[1]  # Q1 (25e percentiel)
q2 <- quartiles[2]  # Q2 (50e percentiel / Mediaan)
q3 <- quartiles[3]  # Q3 (75e percentiel)
q4 <- quartiles[4]  # Q4 (100e percentiel)

# Maak een cumulatieve verdelingsplot met kwartielopvulling
ggplot(data, aes(x = Weight)) +
  # Opvulgebied voor Q1
  stat_ecdf(
    geom = "area",
    aes(
      y = after_stat(y),
      fill = "Q1"
    ),
    bw = 2
  ) +
  # Opvulgebied voor Q2
  stat_ecdf(
    geom = "area",
    aes(
      y = ifelse(
        after_stat(x) > q1 & after_stat(x) <= q2,
        after_stat(y),
        NA
      ),
      fill = "Q2"
    ),
    bw = 2
  ) +
  # Opvulgebied voor Q3
  stat_ecdf(
    geom = "area",
    aes(
      y = ifelse(
        after_stat(x) > q2 & after_stat(x) <= q3,
        after_stat(y),
        NA
      ),
      fill = "Q3"
    ),
    bw = 2
  ) +
  # Opvulgebied voor Q4
  stat_ecdf(
    geom = "area",
    aes(
      y = ifelse(
        after_stat(x) > q3,
        after_stat(y),
        NA
      ),
      fill = "Q4"
    ),
    bw = 2
  ) +
  # Volledige ECDF-curve (consistent over de hele dataset)
  stat_ecdf(
    geom = "step",
    size = 1,
    color = opvulkleur,
    bw = 2
  ) +
  # Voeg aangepaste x-as ticks en labels toe voor de kwartielen
  scale_x_continuous(
    breaks = c(q1, q2, q3),
    labels = c("Q1", "Q2", "Q3"),
    minor_breaks = NULL
  ) +
  # Voeg aangepaste kleuren toe voor de kwartielen
  scale_fill_manual(
    values = c(
      "Q1" = lighten_color(opvulkleur, 0.8),
      "Q2" = lighten_color(opvulkleur, 0.6),
      "Q3" = lighten_color(opvulkleur, 0.4),
      "Q4" = lighten_color(opvulkleur, 0.2)
    )
  ) +
  geom_segment(
    aes(
      x = min(NHANES$Weight, na.rm = TRUE),
      xend = quantiles[1],
      y = 0.25,
      yend = 0.25
    ),
    linetype = "dashed",
    color = "black",
    size = 0.8
  ) +
  geom_segment(
    aes(
      x = min(NHANES$Weight, na.rm = TRUE),
      xend = quantiles[2],
      y = 0.5,
      yend = 0.5
    ),
    linetype = "dashed",
    color = "black",
    size = 0.8
  ) +
  geom_segment(
    aes(
      x = min(NHANES$Weight, na.rm = TRUE),
      xend = quantiles[3],
      y = 0.75,
      yend = 0.75
    ),
    linetype = "dashed",
    color = "black",
    size = 0.8
  ) +
  geom_point(
    aes(
      x = quantiles[1],
      y = 0.25
    ),
    color = "black",
    size = 3
  ) +
  geom_point(
    aes(
      x = quantiles[2],
      y = 0.5
    ),
    color = lijnkleur1,
    size = 3
  ) +
  geom_point(
    aes(
      x = quantiles[3],
      y = 0.75
    ),
    color = "black",
    size = 3
  ) +
  geom_segment(
    aes(
      x = quantiles[1],
      xend = quantiles[3],
      y = 0.1,
      yend = 0.1
    ),
    arrow = arrow(ends = "both", length = unit(0.3, "cm")),
    color = "black",
    size = 0.8,
    lineend = "round"
  ) +
  labs(
    title = NULL,
    x = "Lichaamsgewicht (kg)",
    y = "Cumulatieve proportie",
    fill = "Kwartielen"
  ) +
  theme_minimal() +
  theme(legend.position = "none")  # Verwijder de legenda

Figuur 20.15: Cumulatieve verdeling van lichaamsgewicht in de NHANES-dataset en het IKA. Het eerste, tweede, en derde kwartiel zijn op de \(x\)-as aangegeven. Horizontale onderbroken lijnen laten zien dat de cumulatieve verdelingsfunctie daar gelijk is aan respectievelijk 0,25, 0,5, en 0,75. De zwarte pijl loopt van Q1 naar Q3; zijn lengte is dus de interkwartielafstand.

Statistieken die nauw met de kwartielen samenhangen zijn de percentielen (percentiles). Omdat 25% van de waarnemingen kleiner is dan Q1, wordt Q1 ook wel het vijf-en-twintigste percentiel genoemd, of P25. Op dezelfde manier is 90% van de waarnemingen kleiner dan P90, het negentigste percentiel.

In algemene termen worden statistieken zoals kwartielen en percentielen samen aangeduid als kwantielen (quantiles). We komen die in latere hoofdstukken ook nog tegen.

Note 20.1: Exacte definities van kwantielen zijn gecompliceerd

Als je er dieper over nadenkt is het niet vanzelfsprekend hoe je kwantielen precies moet definiëren. Bijvoorbeeld, stel dat je de kwartielen Q1 en Q3 wilt berekenen maar het aantal waarnemingen niet deelbaar is door 4. Hoe deel je de dataset dan in vier stukken, en waar trek je dan precies de grens tussen de kwartielen?

Voor berekeningen met de hand houdt men meestal deze berekening aan:

• Als het aantal getallen \(n\) even is, dan sorteer je de rij getallen en splitst die vervolgens in twee delen: de grote en de kleine getallen. Q1 is dan de mediaan van de kleine getallen, Q3 de mediaan van de grote getallen.

  Een voorbeeld:

  \[ 1 \quad 3 \underset{\mathrm{Q1} = 3{,}5}{|} 4 \quad 5 \underset{\mathrm{Q2} = 5{,}5}{|} 6 \quad 8 \underset{\mathrm{Q3} = 8{,}5}{|} 9 \quad 10 \]

• Als het aantal getallen \(n\) oneven is, dan sorteer je de rij getallen, haalt de mediaan (Q2) weg, en splitst vervolgens de overige getallen in twee delen: de grote en de kleine getallen. Q1 is dan de mediaan van de kleine getallen, Q3 de mediaan van de grote getallen.

  Voorbeeld:

  \[ 1 \quad 2 \underset{\mathrm{Q1} = 2{,}5}{|} 3 \quad 4 \qquad \underset{\mathrm{Q2} = 5}{5\phantom{|}} \qquad 6 \quad 8 \underset{\mathrm{Q3} = 8{,}5}{|} 9 \quad 10 \]

Als je de berekening met software uitvoert (zie Paragraaf 20.14.2.3), wordt meestal een subtielere berekening uitgevoerd. Als de dataset niet heel klein is, dan zijn de verschillen tussen verschillende definities te verwaarlozen. Maar kijk niet gek op als de kwantielen die R produceert afwijken van jouw eigen berekeningen.

Oefening 20.6 (Opgave: Ligging en spreiding van tentamencijfers)

De scores van 16 studenten op een tentamen zijn als volgt (in volgorde van laag naar hoog):

\[ 12, 15, 18, 20, 21, 23, 25, 28, 30, 32, 35, 38, 40, 42, 45, 46. \]

1. Bereken met de hand de mediaan van deze dataset.

2. Bereken Q1 (het eerste kwartiel) en Q3 (het derde kwartiel) met de hand. (Zie Note 20.1.)

3. Wat is de interkwartielafstand (IKA)?

4. Een student die bij de eerste toets ziek was haalt het tentamen in, en krijgt score 19. Nu zijn er dus 17 cijfers. Wat zijn de Q1, Q2, en Q3 nu?

Variantie

De variantie (variance) van een rij waarnemingen is het gemiddelde van de gekwadrateerde residuen. De formule:

\[ V_X = \frac{\sum_{i=1}^n \left(x_i - \overline{x}\right)^2}{n-1}. \qquad(20.4)\]

• De teller is de kwadratensom die we in Figuur 20.13 al tegenkwamen: de som van de gekwadrateerde afwijkingen ten opzichte van het gemiddelde (\(\overline{x}\)). Door de afwijkingen te kwadrateren, zorgen we ervoor dat positieve en negatieve afwijkingen elkaar niet opheffen.
• In de noemer zou je misschien \(n\) verwachten in plaats van \(n - 1\). De reden waarom hier \(n - 1\) wordt gebruikt kunnen we helaas pas in Paragraaf 21.8 uitleggen; je zult het tot die tijd even moeten aannemen.

Let op de dimensie en eenheid!

De dimensie van de variantie \(V_X\) is het kwadraat van de dimensie van \(X\). Als \(X\) bijvoorbeeld een gewicht is (de dimensie) en gemeten wordt in kilogrammen (de eenheid), dan heeft \(V_X\) de dimensie van gewicht-kwadraat en wordt die uitgedrukt in vierkante kilogrammen (\(\text{kg}^2\)). Dit maakt de variantie lastig te interpreteren. Daarom gebruiken we vaak de standaarddeviatie – de volgende maat op onze lijst!

Standaarddeviatie

De standaarddeviatie (standard deviation, ook wel standaardafwijking genoemd) is waarschijnlijk de meest gebruikte spreidingsmaat. De definitie is eenvoudig: het is de wortel van de variantie: \[ s_X = \sqrt{V_X}. \qquad(20.5)\] Als we de definitie van de variantie invullen levert dat op: \[ s_X = \sqrt{\frac{\sum_{i=1}^n \left(x_i - \overline{x}\right)^2}{n-1}}. \qquad(20.6)\]

In de formule worden de afwijkingen/residuen \((x_i - \overline{x})\) eerst gekwadrateerd en opgeteld, maar uiteindelijk nemen we weer de wortel. Hierdoor heeft de standaarddeviatie dezelfde dimensie als de variabele zelf. Meet je dus een lengte in mm, dan is de standaarddeviatie ook een lengte in mm. Dit maakt de standaarddeviatie gemakkelijker te interpreteren dan de variantie.

Je kunt de standaarddeviatie interpreteren als een “typische” afwijking van het gemiddelde. Het is dus niet verrassend als een willekeurig gekozen waarneming een standaarddeviatie groter of kleiner is dan het gemiddelde. Maar bij de meeste verdelingen is een waarneming die meer dan twee standaarddeviaties van het gemiddelde afligt vrij uitzonderlijk.

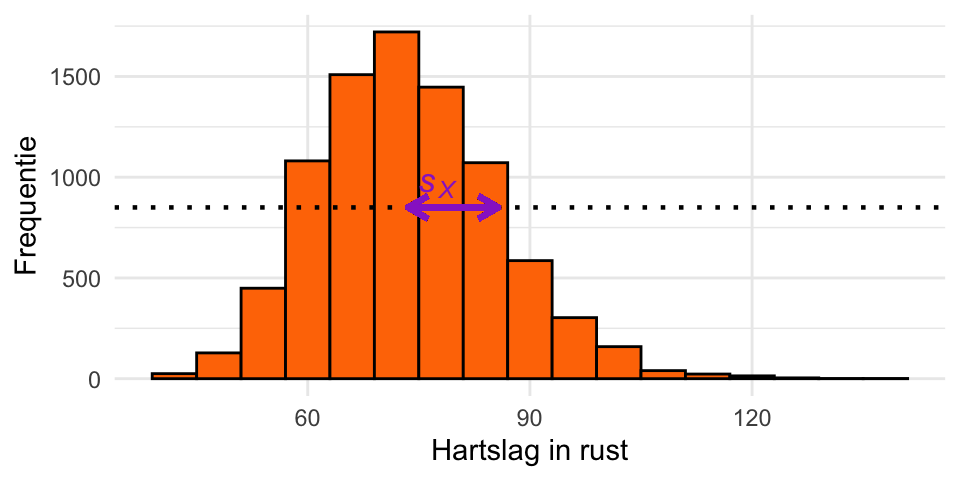
Als voorbeeld nemen we weer een variabele uit de dataset NHANES. Van de mensen die onderzocht zijn is ook de rusthartslag bepaald (Pulse). In Figuur 20.16 is een histogram van die variabele weergegeven. Deze is unimodaal en redelijk klokvormig. Je kunt de standaarddeviatie dan grofweg inschatten als de helft van de breedte van de piek van het histogram, gemeten iets boven de helft van de hoogte van het histogram. In de figuur is de standaarddeviatie met een pijl aangegeven.

# Controleer of de benodigde pakketten zijn geladen
if (!("ggplot2" %in% .packages())) { library(ggplot2) }
if (!("NHANES" %in% .packages())) { library(NHANES) }
if (!("scales" %in% .packages())) { library(scales) }

# Laad de NHANES dataset
data("NHANES")

# Bereken het gemiddelde en de standaarddeviatie van Pulse
mean_pulse <- mean(NHANES$Pulse, na.rm = TRUE)
sd_pulse <- sd(NHANES$Pulse, na.rm = TRUE)

# Automatisch gegenereerde breaks met het gemiddelde toegevoegd
default_breaks <- extended_breaks()(range(NHANES$Pulse, na.rm = TRUE))
all_breaks <- sort(c(default_breaks, mean_pulse))
labels <- ifelse(
  all_breaks == mean_pulse, 
  expression(italic(bar(x))), 
  all_breaks
  )

# Maak een histogram met een binbreedte van 6
ggplot(NHANES, aes(x = Pulse)) +
  geom_histogram(
    binwidth = 6, 
    fill = opvulkleur, 
    color = "black", 
  ) +
  
  # Voeg een verticale stippellijn toe voor het gemiddelde
  #geom_vline(
  #  xintercept = mean_pulse, 
  #  linetype = "dashed", 
  #  color = "black", 
  #  size = 1
  #) +
  
  # Voeg een horizontale stippenlijn toe op de hoogte van de pijl
  geom_hline(
    yintercept = 850, 
    linetype = "dotted", 
    color = "black", 
    size = 0.8
  ) +
  
  # Voeg een horizontale pijl toe om de standaarddeviatie aan te geven
  geom_segment(
    aes(
      x = mean_pulse, 
      xend = mean_pulse + sd_pulse, 
      y = 850, 
      yend = 850
    ),
    arrow = arrow(
      length = unit(0.3, "cm"), 
      ends = "both"
    ), 
    color = "DarkOrchid", 
    size = 1
  ) +
  
  # Voeg een label toe voor de standaarddeviatie (s_X)
  annotate(
    "text", 
    x = mean_pulse + sd_pulse / 2.5 -1, 
    y = 960, 
    label = expression(italic(s[X])), 
    color = "DarkOrchid", 
    size = 4.5, 
    parse = TRUE
  ) +
  
  # Pas de x-as aan met automatische ticks en het gemiddelde als extra
  scale_x_continuous(
    name = "Hartslag in rust",
#    breaks = all_breaks, 
#    labels = labels,
    minor_breaks = NULL # Schakel minor ticks uit
  ) +
  
  # Pas de labels aan
  labs(
    y = "Frequentie"
  ) +
  
  # Gebruik een minimalistisch thema
  theme_minimal()

Figuur 20.16: Histogram van Pulse (rusthartslag) in de NHANES dataset. De standaarddeviatie is aangegeven met een pijl. Deze komt ongeveer overeen met de helft van de breedte van de piek, gemeten iets boven de helft van de hoogte van de piek.

Oefening 20.7 (Oefenen met het sommatieteken en spreidingsmaten)

Het wegen van \(n = 3\) volwassen poezen levert de volgende gewichten op: \(X_1 = 3{,}0\,\)kg, \(X_2 = 3{,}4\,\)kg en \(X_3=4{,}2\),kg.

1. Bereken \(\sum_{i=1}^3 X_i\).
2. Leg uit dat het gemiddelde gewicht \(\overline{X}\) kan worden geschreven als: \[\overline{X} = \frac{\sum_{i=1}^3 X_i}{3}.\] Bereken \(\overline{X}\).
3. Bereken \(\sum_{i=2}^3 X_i\).
4. Bereken \(\sum^n_{i=1} X_i\).
5. Bereken \(\sum^n_{i=1} X_i^2\).
6. Bereken \(\left( \sum^n_{i=1} X_i\right)^2\).
7. Bereken \(\sum^n_{i=1} \left(X_i - \overline{X}\right)\).
8. Bereken \(\sum^n_{i=1} \left(X_i - \overline{X}\right)^2\).
9. Bereken de variantie en de standaarddeviatie van de gewichten. Maak daarbij gebruik van je eerdere antwoorden.

Oefening 20.8 (Standaarddeviaties inschatten)

Schat van alle histogrammen in Figuur 20.8 op het oog de standaarddeviatie. Houd er rekening mee dat uitbijters en staarten van een verdeling sterk bijdragen aan de standaarddeviatie.

Het is geen probleem als je er, zeg, 25% naast zit; het gaat erom dat je een gevoel ontwikkelt bij het concept standaarddeviatie.

Schat ook de interkwartielafstand door in gedachte de histogram in vier delen te verdelen, zoals in Figuur 20.14.

20.9 Wanneer gebruik je welke centrum- en spreidingsmaat?

We hebben drie centrummaten besproken: de modus, de mediaan, en het gemiddelde. Bovendien hebben we vier spreidingsmaten gezien: het bereik, de IKA, de variantie en de standaarddeviatie. Wanneer gebruik je nu welke maat om een rij gegevens samen te vatten?

Een belangrijk verschil tussen de verschillende maten is hoe ze reageren op uitbijters. Het gemiddelde en de standaarddeviatie worden sterk beïnvloed door uitbijters, terwijl de modus, mediaan, en IKA daar vrijwel ongevoelig voor zijn.

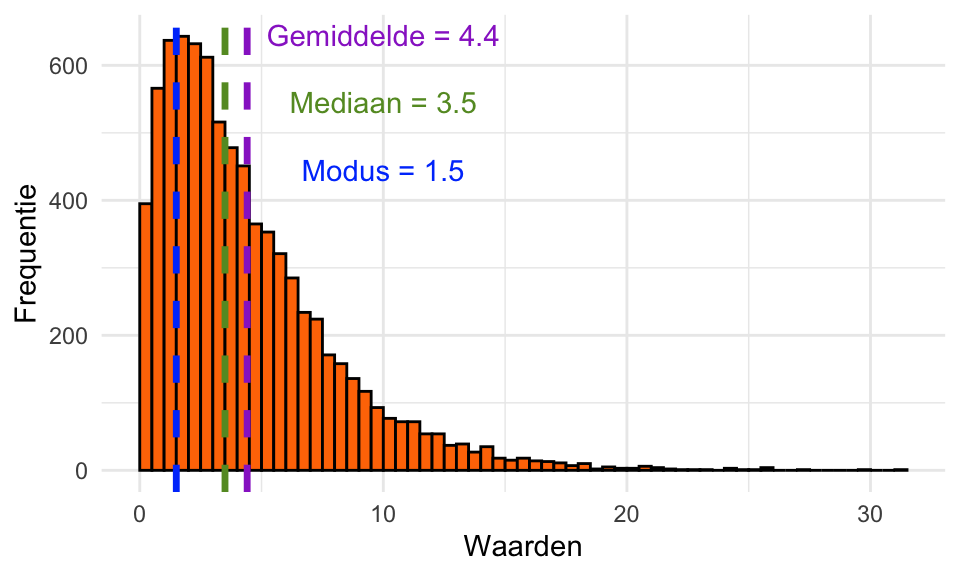
Het gemiddeld en de standaarddeviatie worden ook sterk beïnvloed door de symmetrie van de verdeling. Het histogram in Figuur 20.17 hieronder is rechts-scheef. In zo’n geval is de modus typisch kleiner dan de mediaan en de mediaan kleiner dan het gemiddelde, doordat de rechterstaart een sterk effect heeft op het gemiddelde maar nauwelijks op de andere centrummaten.

# Installeer en laad ggplot2 als het niet al beschikbaar is
if (!("ggplot2" %in% .packages())) {
  library(ggplot2)
}

# Stel een seed in voor reproduceerbaarheid
set.seed(123)

# Parameters voor de Gamma-verdeling
shape <- 1.5        # Vormparameter (k)
scale <- 3          # Schaalparameter (θ)
sample_size <- 8000 # Aantal observaties

# Trek een steekproef uit de Gamma-verdeling
gamma_sample <- rgamma(sample_size, shape = shape, scale = scale)

# Bereken statistieken
mean_value <- mean(gamma_sample)
median_value <- median(gamma_sample)

# Modus berekening voor een Gamma-verdeling
mode_value <- (shape - 1) * scale

# Zet de data in een dataframe voor ggplot2
gamma_df <- data.frame(
  value = gamma_sample
)

# Maak een histogram en voeg verticale lijnen en labels toe
ggplot(gamma_df, aes(x = value)) +
  geom_histogram(
    binwidth = 0.5,
    boundary = 0,
    fill = opvulkleur,
    color = "black",
  ) +
  geom_vline(
    aes(xintercept = mean_value),
    color = lijnkleur1,
    linetype = "dashed",
    size = 1.2
  ) +
  geom_vline(
    aes(xintercept = median_value),
    color = lijnkleur4,
    linetype = "dashed",
    size = 1.2
  ) +
  geom_vline(
    aes(xintercept = mode_value),
    color = lijnkleur3,
    linetype = "dashed",
    size = 1.2
  ) +
  annotate(
    "text",
    x = 10,
    y = 630,
    vjust = 0,
    label = paste0("Gemiddelde = ", round(mean_value, 1)),
    color = lijnkleur1
  ) +
  annotate(
    "text",
    x = 10,
    y = 530,
    vjust = 0,
    label = paste0("Mediaan = ", round(median_value, 1)),
    color = lijnkleur4
  ) +
  annotate(
    "text",
    x = 10,
    y = 430,
    vjust = 0,
    label = paste0("Modus = ", round(mode_value, 1)),
    color = lijnkleur3
  ) +
  labs(
    title = NULL,
    x = "Waarden",
    y = "Frequentie"
  ) +
  theme_minimal()

Figuur 20.17: Voorbeeld van een scheve verdeling, waarbij de modus, de mediaan, en het gemiddelde zijn aangegeven. Bij zo’n rechts-scheve verdeling is typisch de modus kleiner dan de mediaan, en de mediaan kleiner dan het gemiddelde.

Daarom gebruiken we de volgende richtlijnen.

Situatie 1: De verdeling van gegevens is grofweg symmetrisch en er zijn geen opvallende uitbijters. In dat geval is het beste het gemiddelde en de standaarddeviatie te rapporteren.

Situatie 2: De verdeling van gegevens is scheef en/of er zijn opvallende uitbijters. In dat geval kun je het beste de mediaan en de IKA rapporteren.

20.10 Verdelingen samenvatten met frequentietabellen

De verdeling van een variabele wordt vaak samengevat door middel van een frequentietabel (frequency table). Dat is een tabel die aangeeft hoe vaak een waarde in een bepaalde categorie of klasse valt. De manier waarop je een frequentietabel opstelt, hangt af van het type variabele.

Frequentietabellen voor categorische variabelen

We beginnen met categorische variabelen.

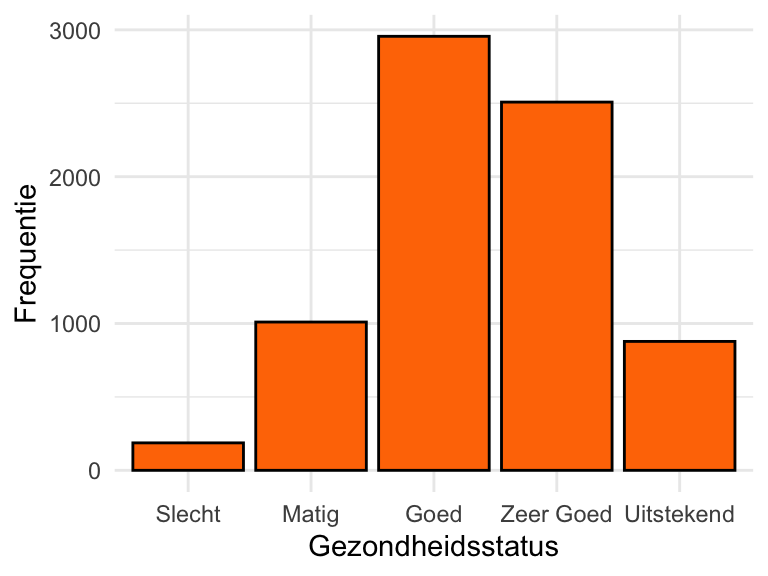
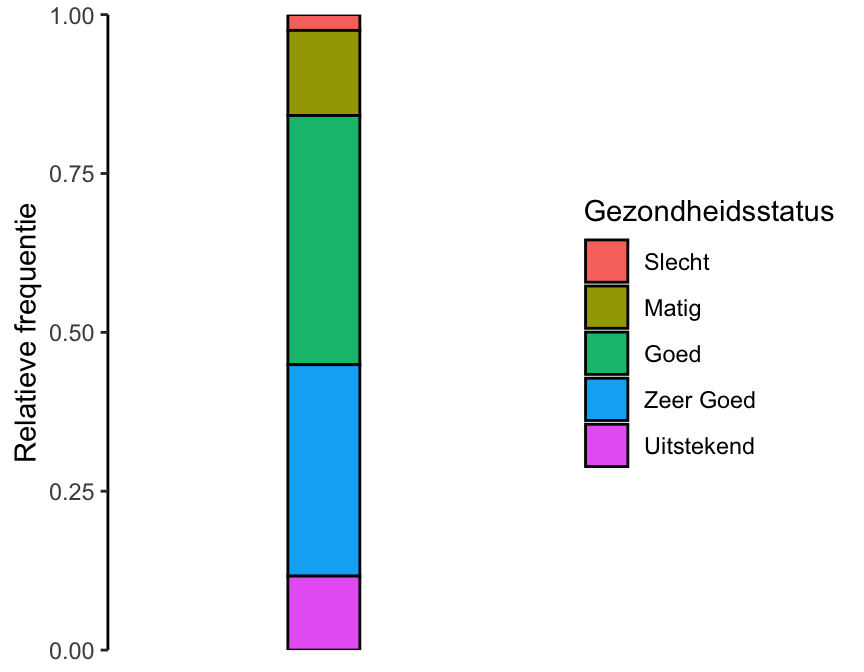
De dataset NHANES bevat ook gegevens over de gezondheidsstatus van de deelnemers aan het onderzoek (HealthGen). De niveaus zijn Slecht, Matig, Goed, Zeer Goed, of Uitstekend. Gezondheidsstatus is hier dus een ordinale variabele. De frequentietabel van deze variabele ziet er als volgt uit:

Tabel 20.2: Frequentietabel van gezondheidsstatus in de dataset NHANES.

Gezondheidsstatus	Absolute frequentie	Relatieve frequentie
Slecht	187	0.02
Matig	1010	0.13
Goed	2956	0.39
Zeer Goed	2508	0.33
Uitstekend	878	0.12

Voor elk niveau van gezondheidsstatus wordt zowel de frequentie weer gegeven; in dit geval zowel de absolute frequentie als de relatieve frequentie. De absolute frequentie geeft aan hoe vaak een niveau voorkomt; de relatieve frequentie drukt dat uit als fractie van het totaal. Zo’n fractie of proportie is een getal tussen 0 en 1, soms uitgedrukt als een percentage.

Het nut van de frequentietabel: een dataset met duizenden regels is samengevat in een tabel met 5 regels, zonder dat daarbij informatie verloren ging. Bovendien zijn de gegevens nu veel beter te overzien. Het valt nu op dat meeste mensen hun eigen gezondheid positief beoordelen (Goed, Zeer Goed, of Uitstekend). In de ruwe data springt die conclusie niet direct in het oog.

Frequentietabel voor continue variabelen

Het opstellen van een frequentietabel voor een numerieke variabele is minder vanzelfsprekend.

in de dataset NHANES is van alle deelnemers ook hun gewicht gegeven in kg, tot op één decimaal. Er zijn erg veel verschillende waarden gemeten; tellen hoe vaak iedere waarde voorkomt levert dus geen nuttige samenvatting op. Dit probleem speelt bij alle continue variabelen.

De oplossing is om de gegevens op te delen in intervallen, die klassen (bins) worden genoemd. Voor iedere klasse tellen we hoe vaak een waarneming erin valt. Voor de gewichten levert dat de volgende tabel op:

Tabel 20.3: Frequentietabel van de lichaamsgewichten in de dataset NHANES.

Lichaamsgewicht (kg)	Absolute frequentie
[0,10)	133
[10,20)	618
[20,30)	424
[30,40)	288
[40,50)	448
[50,60)	1068
[60,70)	1547
[70,80)	1630
[80,90)	1416
[90,100)	939
[100,110)	691
[110,120)	355
[120,130)	174
[130,140)	86
[140,150)	49
[150,160)	11
[160,170)	26
[170,180)	6
[180,190)	6
[190,200)	2
[200,210)	1
[210,220)	0
[220,230)	2

De lastigste stap is het kiezen van de klassen. Je moet namelijk besluiten hoe breed je de klassen maakt en op welke plek je ze laat beginnen. Hiervoor zijn allerlei formele regels voorgesteld, maar met gezond verstand kom je een heel eind.

• Ronde getallen zijn overzichtelijk.
• Als je heel brede intervallen gebruikt, veeg je veel gegevens op één hoop; dat kan belangrijke patronen in je data onzichtbaar maken. Aan de andere kant, als je heel smalle intervallen gebruikt, wordt de tabel onoverzichtelijk lang en het aantal waarnemingen per klasse erg klein. Het is dus zoeken naar een middenweg.

Frequentietabellen voor discrete variabelen

Bij discrete variabelen hangt de aanpak af van het aantal mogelijke waarden. Als dat er weinig zijn (zoals het aantal kinderen per gezin: meestal 0 t/m 3), tel je de frequentie van iedere waarde, net als bij categorische variabelen. Als de waarden verspreid zijn over een groot bereik (zoals het aantal inwoners per land), deel je ze in klassen in, net als bij continue variabelen.

Oefening 20.9 (Gewogen gemiddelden)

Deze opgave is bedoeld als voorbereiding voor Oefening 20.10.

Je hebt voor de tentamens van een vak een 5, een 8, en een 7 gehaald. Het eerste cijfer telt mee voor 10%, het tweede voor 60%, en het derde voor 30%. Bereken het (gewogen) gemiddelde. Schrijf op hoe je dat berekent.

Oefening 20.10 (Gemiddelden berekenen op basis van een frequentietabel.)

Je bent een middagje naar de vogeltrek aan het kijken en wilt graag weten hoe groot de zwermen vogels meestal zijn. Telkens als er een zwerm overvliegt tel je het aantal vogels dat erin zit. Uiteindelijk heb je de volgende 10 waarnemingen:

\[5 \quad 3\quad 6\quad 2\quad 4\quad 3\quad 3\quad 2\quad 2\quad 5\]

1. Bereken het gemiddeld aantal vogels in een zwerm.

Je kunt de waarnemingen ook weergeven in een frequentietabel:

Aantal vogels	Frequentie	Relatieve frequentie
2	3	0,3
3	3	0,3
4	1	0,1
5	2	0,2
6	1	0,1

2. Leg uit dat het gemiddelde ook zo berekend kan worden: \[ \overline{x} = \frac{3\times {\color{darkorange}2} + 3\times {\color{darkorange}3} + 1\times {\color{darkorange}4} + 2\times {\color{darkorange}5} + 1 \times {\color{darkorange}6} }{10}.\] Wat stelt het eerste getal in de vermenigvuldigingen steeds voor?

3. Leg uit dat het gemiddelde ook zo berekend kan worden: \[ \overline{x} = {\color{darkorchid}0{,}3}\times {\color{darkorange}2} + {\color{darkorchid}0{,}3}\times {\color{darkorange}3} + {\color{darkorchid}0{,}1}\times {\color{darkorange}4} + {\color{darkorchid}0{,}2}\times {\color{darkorange}5} + {\color{darkorchid}0{,}1}\times {\color{darkorange}6}.\] Wat stelt het eerste getal in de vermenigvuldigingen nu voor?

4. Stel dat de relatieve frequentie van de waarde \(x\) genoteerd wordt als \({\color{darkorchid}f(x)}\). Leg uit dat het gemiddelde dan altijd zo kan worden geschreven: \[ \overline{x} = \sum_{\color{darkorange}x} {\color{darkorchid}f(x)} {\color{darkorange}x}. \qquad(20.7)\] Met de notatie \(\sum_x\) wordt gedoeld dat je moet sommeren over alle waarden van \(x\) die kunnen voorkomen.

5. Wat is de relatie tussen Vergelijking 20.7 en Oefening 20.9?

Relatieve frequenties en gewogen gemiddelden

In Oefening 20.10 heb je geleerd hoe je het gemiddelde kan berekenen van waarnemingen die zijn samengevat in een frequentietabel. Vergelijking 20.7 is eigenlijk gemakkelijk te begrijpen: het is een gewogen gemiddelde, waarbij je voor het gewicht van iedere mogelijke uitkomst de relatieve frequentie gebruikt.

Het is handig als je dit goed begrijpt: dat komt van pas als we het in Hoofdstuk 22 gaan hebben over het gemiddelde van kansverdelingen.

20.11 Het visualiseren van verdelingen van categorische variabelen

Het is bijna altijd nuttig om de verdeling van een variabele te visualiseren. Daar zijn verschillende technieken voor. Welke techniek gebruikt kan worden, hangt af van het type van de variabele.

Staafdiagrammen

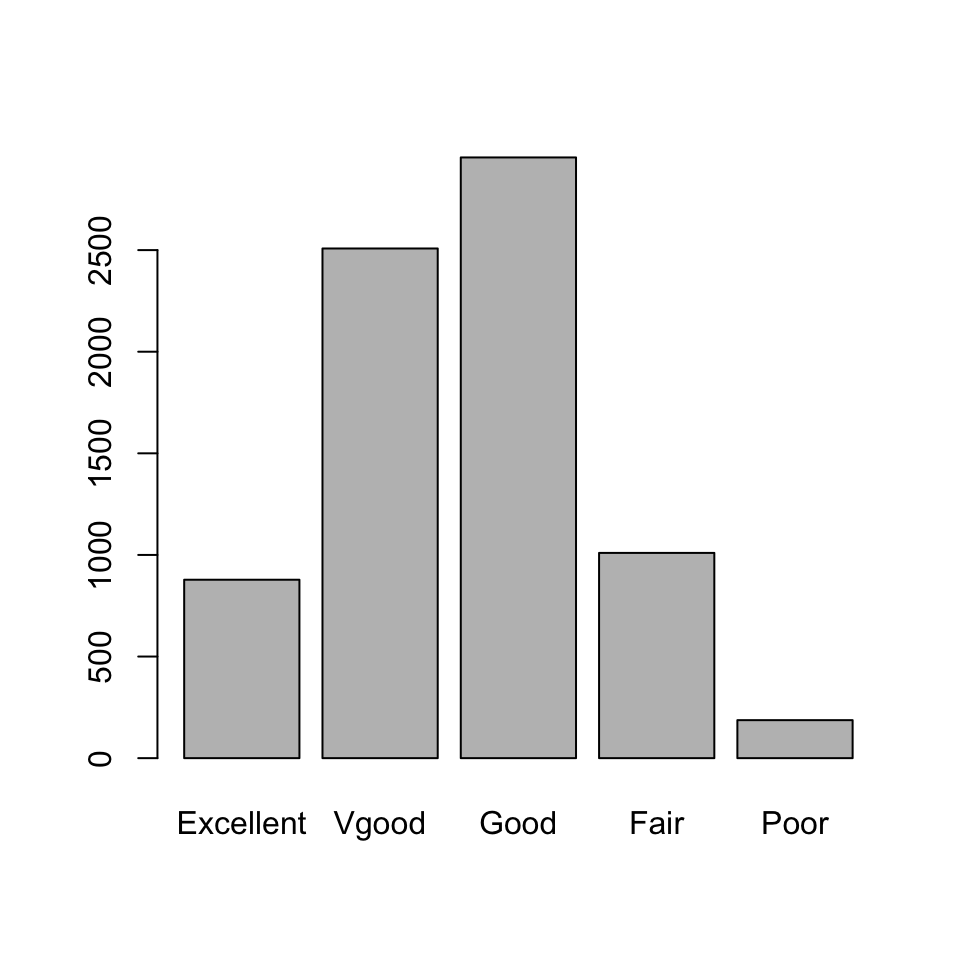
Als de variabele categorisch is, wordt vaak een staafdiagram (bar graph) gebruikt. Het idee is om de frequenties van ieder niveau weer te geven als de oppervlakte van een staaf. Zo is het op het oog direct duidelijk welke categorieën de hoogste frequentie hebben. Figuur 20.18 is een staafdiagram voor de variabele gezondheidsstatus van de dataset NHANES.

# De gegevens zijn gepubliceerd in dit package:
library(NHANES)
library(ggplot2)
library(knitr)
library(dplyr)


# Laad de dataset in:
data(NHANES)

# Eerst: de variabele `HealthGen` (gezondheidsstatus)

# Vertaal de levels en zet ze in een logische volgorde:
NHANES$HealthGen <- factor(
  NHANES$HealthGen,
  levels = c("Poor", "Fair", "Good", "Vgood", "Excellent"),
  labels = c("Slecht", "Matig", "Goed", "Zeer Goed", "Uitstekend"),
  ordered = TRUE
  )

# We filteren de regels met missende waarden voor Gezondheidsstatus:
NHANES_filtered <- NHANES %>% filter(!is.na(HealthGen))

# Maak een frequentietabel en laat die zien.

freq_table <- table(NHANES$HealthGen)
tot_table <- addmargins(freq_table)

# Maak een staafdiagram:
ggplot(
  data = NHANES_filtered, 
  aes(x = HealthGen)
  ) +
  geom_bar(
    fill = opvulkleur, 
    color = "black"
    ) +
  labs(
    title = NULL,
    x = "Gezondheidsstatus",
    y = "Frequentie"
    ) +
  theme_minimal()

Figuur 20.18: Staafdiagram van gezondheidsstatus (HealthGen) in de gegevensvan het NCHS-onderzoek.

Let bij het maken van een staafdiagram op drie dingen.

1. Laat de \(y\)-as altijd op 0 beginnen. Als je de \(y\)-as “afsnijdt”, zijn de oppervlaktes van de staven niet meer representatief voor de frequenties die ze voorstellen. Op het oog lijken de verschillen tussen de frequenties dan veel groter dan ze daadwerkelijk zijn. Het volgende voorbeeld laat duidelijk zien hoe misleidend dat kan zijn.

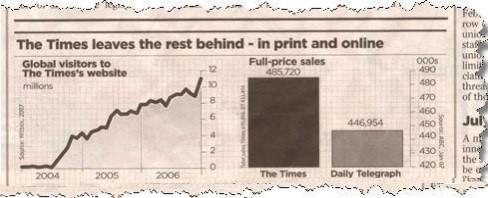
Voorbeeld 20.4 (The Times leaves the rest behind) Het volgende krantenknipsel laat zien dat De Times beter verkoopt dan de Daily Telegraph:

Maar kijk eens goed naar het staafdiagram aan de rechterkant. Op het eerste gezicht lijkt het verschil in full-price sales enorm omdat de staaf van The Times een veel groter oppervlakte heeft dan die van de Telegraph. (Die indruk wordt ook nog versterkt door het verschil in de kleur!) Pas als je naar de \(y\)-as kijkt, blijkt het verschil nogal mee te vallen.

2. Houd ruimte tussen de staven. Dat laat zien dat de categorieën van een categorische variabele niet geleidelijk in elkaar overlopen maar los van elkaar staan.

3. Kies de volgorde van de staven verstandig. Bij ordinale variabelen hou je de natuurlijke volgorde van de niveaus aan, zoals in Figuur 20.18. Bij nominale variabelen is het vaak overzichtelijk om te sorteren op frequentie, met de belangrijkste categorieën eerst, maar soms is een alfabetische volgorde handiger.

Taart- en stapeldiagrammen

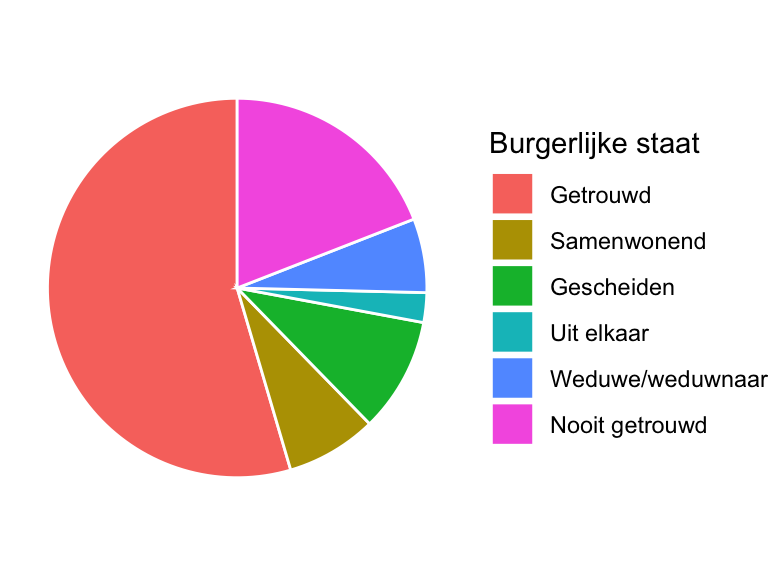
Een alternatief is het taartdiagram (pie chart). Een taartdiagram geeft de relatieve frequenties van de niveaus weer als sectoren van een cirkel. Figuur 20.19 laat een voorbeeld zien: de verdeling van burgerlijke staat in de dataset NHANES. Meer dan de helft van de personen in de steekproef blijkt getrouwd te zijn.

NHANES$MaritalStatus <- factor(
  NHANES$MaritalStatus,
  levels = c("Married", "LivePartner", "Divorced", "Separated", "Widowed", "NeverMarried"),
  labels = c("Getrouwd", "Samenwonend", "Gescheiden", "Uit elkaar", "Weduwe/weduwnaar", "Nooit getrouwd"),
  ordered = TRUE
  )

table_MaritalStatus <- table(NHANES$MaritalStatus)

data <- data.frame(
  table_MaritalStatus
)
colnames(data) <- c("BurgerlijkeStaat", "Frequentie")

# Taartdiagram
ggplot(
  data, 
  aes( 
    x = "", 
    y = Frequentie, 
    fill = BurgerlijkeStaat
    )
  ) +
  geom_bar(
    stat="identity", 
    width = 1, 
    color = "white"
  ) +
  coord_polar( "y", start = 0 ) +
  labs( fill = "Burgerlijke staat") +
  theme_void()

Figuur 20.19: Taartdiagram van burgerlijke staat in de dataset NHANES.

Gebruik een taartdiagram alleen als je de relatieve frequenties van niveaus wilt benadrukken, want de absolute frequenties zijn niet af te lezen.

Voor ordinale variabelen zijn taartdiagrammen niet erg geschikt: die hebben van nature een eerste en een laatste categorie, wat niet te zien is bij een cirkelvormige weergave. Een stapeldiagram is dan een betere optie. Daarbij worden de frequenties weergegeven als opgestapelde staven. Figuur 20.20 laat als voorbeeld het stapeldiagram zien voor de variabele gezondheidsstatus van de dataset NHANES.

freq_df <- data.frame(
  freq_table
)
colnames(freq_df) <- c("Gezondheidsstatus", "Frequentie")

ggplot(
  freq_df, 
  aes( 
      x = "", 
      y = Frequentie/nrow(NHANES_filtered), 
      fill = Gezondheidsstatus
      )
  ) +
  geom_bar(
    position = "stack", 
    stat="identity", 
    width = 0.2, 
    color="black"
  ) + 
  theme_classic() + 
  labs( x = "", y = "Relatieve frequentie") +
  theme(
    axis.title.x = element_blank(),  # Remove x-axis title
    axis.text.x = element_blank(),   # Remove x-axis text/labels
    axis.ticks.x = element_blank(),   # Remove x-axis ticks
    axis.line.x = element_blank()
  ) +
  scale_y_continuous(limits = c(0, 1), expand = c(0, 0))

Figuur 20.20: Stapeldiagram van de variabele Gezondheidsstatus in de dataset NHANES.

20.12 Het visualiseren van verdelingen van numerieke variabelen

Na het verkennen van methoden voor categorische variabelen, richten we ons nu op technieken om numerieke variabelen te visualiseren.

Histogrammen en frequentiepolygonen

Histogrammen zijn we eerder in dit hoofdstuk al vaak tegengekomen. Histogrammen lijken op staafdiagrammen, maar zijn bedoeld voor numerieke variabelen in plaats van categorische.

zijn voor categorische variabelen. Bij een staafdiagram laat je ruimte tussen de staven om te laten zien dat de categorieën los van elkaar staan; bij een histogram juist niet, omdat de klassen in elkaar overlopen.

Net als bij staafdiagrammen is het belangrijk dat de \(y\)-as altijd bij 0 begint, omdat anders de oppervlaktes van de staven niet meer proportioneel zijn met de frequenties die ze representeren.

Je kunt exact dezelfde gegevens ook presenteren als frequentiepolygoon. Figuur 20.21 is een voorbeeld, voor de variabele lichaamsgewicht. De frequentie van iedere gewichtsklasse wordt uitgezet tegen het midden van die gewichtsklasse, en vervolgens wordt een lijn getrokken tussen deze punten.

ggplot(NHANES, aes(x = Weight)) +
  geom_freqpoly(binwidth = 5, color = opvulkleur, size = 1) +
  labs(title = "",
       x = "Lichaamsgewicht (kg)",
       y = "Frequentie") +
  theme_minimal()

Figuur 20.21: Frequentiepolygoon van de lichaamsgewichten uit de dataset NHANES.

Vioolplot

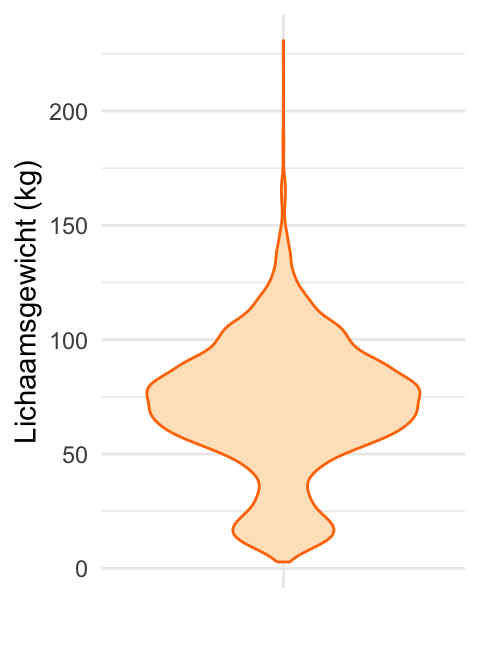
Een vioolplot is aan andere grafische weergave die de verdeling van een numerieke variabele toont. Als voorbeeld is in Figuur 20.22 een vioolplot weergegeven voor de variabele lichaamsgewicht.

• Een vioolplot wordt meestal verticaal weergegeven. Dat wil zeggen, de variabele staat op de \(y\)-as.
• De breedte van de “viool” geeft de frequentie aan: hoe breder de viool op een bepaald punt, hoe meer waarnemingen er zijn bij die waarde.
• De frequentie die bij een waarde hoort wordt niet direct geteld, maar geschat door het aantal punten te tellen in de buurt van die waarde. Dat resulteert in een vloeiende vorm. Hoe groot de “buurt” is die wordt meegenomen wordt bepaald door een parameter die de bandwidth wordt genoemd. Software kiest vaak automatisch een geschikte waarde voor de bandwidth, maar je kunt deze aanpassen om meer of minder detail te laten zien, vergelijkbaar met de breedte van de staven in een histogram.

ggplot(NHANES, aes(x = "", y = Weight)) +
  geom_violin(fill = "Bisque", color = opvulkleur) +
  labs(title = NULL,
       x = "",
       y = "Lichaamsgewicht (kg)") +
  theme_minimal()

Figuur 20.22: Vioolplot van lichaamsgewicht uit de dataset NHANES.

De boxplot

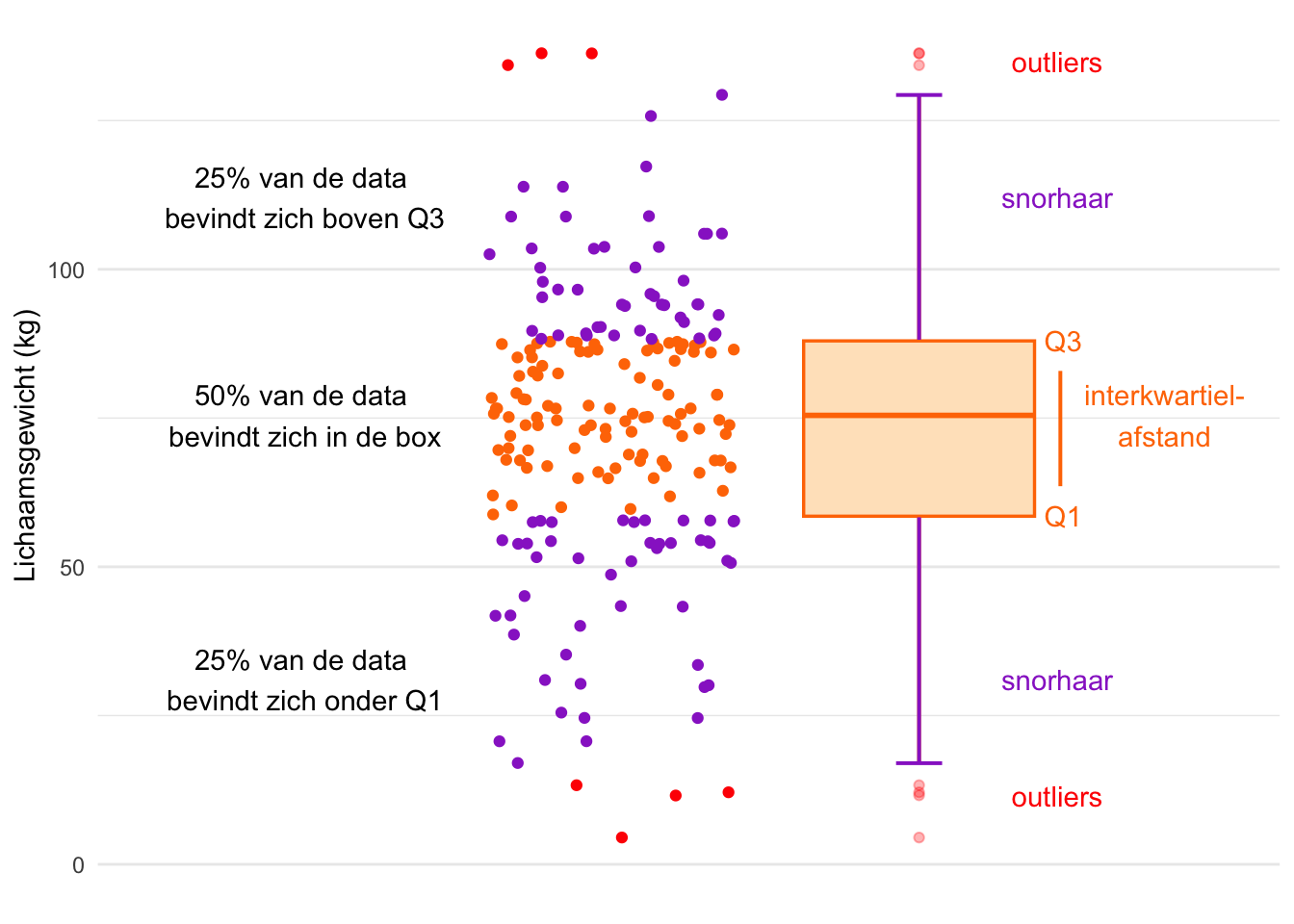
Voor het verkennen en vergelijken van datasets worden vaak boxplots gebruikt. Een boxplot is een compacte grafische weergave die een verdeling samenvat aan de hand van vijf kengetallen plus eventuele uitbijters.

De anatomie van een boxplot is geïllustreerd in Figuur 20.23. Aan de linkerkant zijn de ruwe data weergegeven als een puntenwolk. Dit wordt een jitterplot genoemd. Aan de rechterkant zie je de bijbehorende boxplot.

# Data voorbereiden
data <- NHANES[1:200, ]
data <- data[order(data$Weight), ]
kwantielen <- quantile(data$Weight)
kwantielen[1] <- kwantielen[1] - 1  # Aanpassing voor visualisatie
interkwartielafstand <- kwantielen[4] - kwantielen[2]
uitbijters <- c(
  kwantielen[2] - 1.5 * interkwartielafstand,
  kwantielen[4] + 1.5 * interkwartielafstand
)
grenzen <- c(kwantielen, uitbijters)

# Plot
ggplot(data, aes(x = "", y = Weight)) +
  # Boxplot
  geom_boxplot(
    aes(x = 3), 
    fill = "Bisque", 
    color = opvulkleur,
    size = 0.7,
    outlier.color = "red",
    outlier.alpha = 0.3
  ) +
  stat_boxplot(
    aes(x = 3),
    geom = "errorbar",
    colour = "DarkOrchid",
    size = 0.7,
    width = 0.15
  ) +
  geom_boxplot(
    aes(x = 3), 
    fill = "Bisque", 
    color = opvulkleur,
    coef = 0, 
    outlier.shape = NA
  ) +
  # Jitterplot
  geom_jitter(
    aes(
      x = 2, 
      col = cut(data$Weight, grenzen)
    )
  ) +
  # Annotaties
  annotate(
    "text", 
    y = kwantielen[2], 
    x = 3.47, 
    label = "Q1", 
    color = opvulkleur
  ) +
  annotate(
    "text", 
    y = kwantielen[4], 
    x = 3.47, 
    label = "Q3", 
    color = opvulkleur
  ) +
  annotate(
    "text", 
    y = kwantielen[3], 
    x = 3.8, 
    label = "interkwartiel-
afstand", 
    color = opvulkleur
  ) +
  annotate(
    "text", 
    y = mean(kwantielen[4:5]), 
    x = 3.45, 
    label = "snorhaar", 
    color = "DarkOrchid"
  ) +
  annotate(
    "text", 
    y = mean(kwantielen[1:2]), 
    x = 3.45, 
    label = "snorhaar", 
    color = "DarkOrchid"
  ) +
  annotate(
    "segment",
    y = kwantielen[2] + 5, 
    yend = kwantielen[4] - 5,
    x = 3.46,
    size = 0.7,
    color = opvulkleur
  ) +
  annotate(
    "text", 
    y = uitbijters + c(-3, 3), 
    x = 3.45, 
    label = "uitbijters", 
    color = "red"
  ) +
  annotate(
    "text", 
    y = kwantielen[3], 
    x = 1, 
    label = "50% van de data 
bevindt zich in de box"
  ) +
  annotate(
    "text", 
    y = mean(kwantielen[1:2]), 
    x = 1, 
    label = "25% van de data 
bevindt zich onder Q1"
  ) +
  annotate(
    "text", 
    y = mean(kwantielen[4:5]), 
    x = 1, 
    label = "25% van de data 
bevindt zich boven Q3"
  ) +
  # Labels en thema
  labs(
    title = NULL,
    x = "",
    y = "Lichaamsgewicht (kg)"
  ) +
  theme_minimal() +
  scale_x_continuous(
    breaks = NULL, 
    limits = c(0.5, 4)
  ) + 
  scale_colour_manual(
    values = c("red", "DarkOrchid", opvulkleur, opvulkleur, "DarkOrchid", "red")
  ) +
  theme(legend.position = "none")

Figuur 20.23: Anatomie van een boxplot. Links is van een steekproef uit de dataset NHANES het lichaamsgewicht geplot als een jitterplot. Daarnaast is de bijbehorende boxplot weergegeven.

Een boxplot bestaat uit verschillende elementen die elk een specifiek aspect van de verdeling van de variabele weergeven.

1. De mediaan:
   De mediaan, oftewel Q2 wordt weergegeven met een horizontale streep.

2. De box:
   Om de mediaan wordt een rechthoek getekend – de “box”. Deze rechthoek loopt van Q1 naar Q3, waarbinnen de middelste 50% van de data zich bevindt. De hoogte van de box vertegenwoordigt dus de interkwartielafstand (IKA).

3. Uitbijters:
   Waarden die meer dan \(1{,}5\) keer de IKA buiten de box liggen, worden als uitbijters beschouwd. Deze datapunten worden afzonderlijk weergegeven, vaak als kleine stippen. Dit maakt uitbijters makkelijk herkenbaar.

4. Snorharen:
   De lijnen die vanuit het midden van de box naar boven en naar beneden lopen worden snorharen (whiskers) genoemd. Ze eindigen bij de verste datapunten die géén uitbijters zijn. De uiteinden van de whiskers geven dus aan waar de “normale” gegevens ophouden en de uitbijters beginnen.

De boxplot laat in één oogopslag een aantal belangrijke kenmerken van de verdeling zien, zoals de mediaan en de IKA. Ook helpt een boxplot bij het beoordelen of een verdeling scheef is. Bij een rechtsscheve verdeling zijn de snorharen aan de bovenkant vaak langer dan aan de onderkant en ligt de mediaan onder het midden van de box. Bovendien zijn er dan vaak meer uitbijters aan de bovenkant dan aan de onderkant.

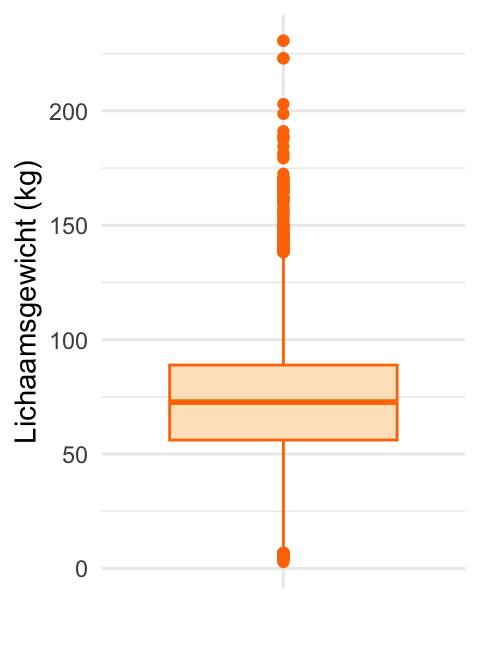
Naast deze voordelen hebben boxplots ook beperkingen. Doordat boxplots grote datasets samenvatten met een klein aantal kengetallen kunnen ze belangrijke details verbergen. Kijk als voorbeeld eens naar Figuur 20.24, waarin de boxplot van de lichaamsgewichten van de NHANES dataset is weergegeven. Eerder hebben we in Figuur 20.21 gezien dat de verdeling van lichaamsgewicht bimodaal is. Die belangrijke eigenschap is in de boxplot niet te zien. Een histogram, vioolplot of frequentiepolygoon geeft in zulke gevallen meer inzicht.

Een boxplot kan ook misleidend zijn bij datasets met weinig waarnemingen. Het heeft niet veel zin om een dataset met zes datapunten samen te vatten in vijf kengetallen (plus uitbijters). Bij kleine datasets is het vaak beter om individuele datapunten weer te geven, bijvoorbeeld met een jitterplot (zoals in Figuur 20.23).

ggplot(NHANES, aes(x = "", y = Weight)) +
  geom_boxplot(fill = "Bisque", color = opvulkleur) +
  labs(title = NULL,
       x = "",
       y = "Lichaamsgewicht (kg)") +
  theme_minimal()

Figuur 20.24: Boxplot van lichaamsgewicht in de dataset NHANES. De bimodaliteit is van de variabele is in deze representatie niet zichtbaar.

Oefening 20.11 (Nationale Tuinvogeltelling)

Een bioloog doet mee aan de Nationale Tuinvogeltelling en telt hoeveel vogels van elke soort ze in een uur in haar tuin ziet. Welke grafiek zou ze het best kunnen gebruiken om de verdeling van vogelsoorten weer te geven?

A een histogram

B een cumulatieve frequentiepolygoon

C een boxplot

D een staafdiagram

Oefening 20.12 (Zetelverdeling tweede kamer)

Je wilt in een figuur laten zien hoe de zetels van de Tweede Kamer verdeeld zijn over de partijen.

1. Welk van de diagrammen die we in dit hoofdstuk behandeld hebben lijkt je daarvoor het meest geschikt?

2. Zie de visualisatie hieronder, afkomstig van Wikipedia. Wat zijn de voor- en nadelen van deze representatie?

Zetelverdeling Tweede Kamer in februari 2025. Screenshot van Wikipedia, CC BY-SA 4.0

20.13 Alles samen: het beschrijven van de verdeling van een variabele

We hebben hierboven een groot aantal begrippen en technieken beschreven. Hoe pas je die informatie nu specifiek toe bij het beschrijven van een verdeling?

De verdeling van numerieke gegevens beschrijven

Als je een lijst numerieke gegevens wilt beschrijven maak je tenminste gebruik van:

• Een visualisatie. Dat kan een jitterplot zijn (bij kleine datasets), een boxplot (als dit geen belangrijke eigenschappen van de gegevens verbergt), een histogram, een frequentiepolygoon, of een vioolplot.
• Een centrummaat. Bij grofweg symmetrische verdelingen zonder extreme uitbijters is het gemiddelde het meest geschikt, en anders de mediaan of de modus.
• Een spreidingsmaat. Bij grofweg symmetrische verdelingen zonder extreme uitbijters is de standaarddeviatie het meest nuttig, en anders de IKA.

De verdeling van categorische gegevens beschrijven

Wil je een lijst categorische gegevens beschrijven, maak dan tenminste gebruik van:

• Een visualisatie. Als je alleen de relatieve frequenties wilt benadrukken en de variabelen nominaal is, dan is een taartdiagram geschikt. Anders ligt een staafdiagram of stapeldiagram meer voor de hand.
• Een frequentietabel.

20.14 Beschrijvende statistiek in R

Hieronder geven we kort aan hoe je verschillende technieken uit dit hoofdstuk in R kunt toepassen.

Typen variabelen in R

In Paragraaf 2.1 heb je geleerd dat variabelen in R ook verschillende types hebben, zoals numeric, integer, of character. Deze typen komen niet één op één overeen met de indeling van Figuur 20.1. Wat is de relatie tussen Figuur 20.1 en de data-typen van R?

Voor numerieke variabelen gebruik je het datatype numeric, waarin getallen met decimalen (“kommagetallen”, floats) kunnen worden opgeslagen. Op zich kan numeric ook voor discrete numerieke variabelen worden gebruikt, maar als de variabele alleen gehele getallen kan aannemen is integer geschikter.

Voor categorische variabelen kan het type character worden gebruikt. Maar in R bestaat ook in een datastructuur die speciaal bedoeld is voor categorische data: de factor.

Categorische gegevens in R: de factor

Om te illustreren wat een factor is, definiëren we in R eerst een vector van type character:

# Vector met de voedingsstrategie van 5 organismen:
voedingsstrategie <- c("herbivoor", "carnivoor", "omnivoor", "detrivoor", "herbivoor")
voedingsstrategie

[1] "herbivoor" "carnivoor" "omnivoor"  "detrivoor" "herbivoor"

Bekijk de uitvoer; je kunt daaraan zien dat voedingsstrategie simpelweg een lijstje (vector) met strings is.

Deze vector van type character zetten we nu om naar een factor en slaan die op onder de naam factor.voedingsstrategie:

# Omzetten naar een factor-variabele:
factor.voedingsstrategie <- factor(voedingsstrategie)
factor.voedingsstrategie

[1] herbivoor carnivoor omnivoor  detrivoor herbivoor
Levels: carnivoor detrivoor herbivoor omnivoor

De uitvoer ziet er subtiel anders uit. De vijf verschillende waarden worden weer getoond, maar er is nu een extra regel die begint met het woord “Levels”. Op die regel worden de verschillende niveaus van de categorische variabele weergegeven. In dit geval waren dat “carnivoor”, “detrivoor”, “herbivoor” en “omnivoor”. Je kunt de niveaus ook rechtstreeks opvragen met de functie levels():

levels(factor.voedingsstrategie)

[1] "carnivoor" "detrivoor" "herbivoor" "omnivoor" 

Oefening 20.13 (Factors en niveaus)

In de code hieronder wordt een dataframe geconstrueerd met daarin gegevens over meerdere spelers van een videogame. Eerst worden de gegevens opgeslagen in meerdere vectoren; daarna worden ze samengevoegd tot een dataframe.

naam <- c("Mario", "Luigi", "Peach", "Toad", "Bowser")
level <- c(8, 1, 3, 2, 10)
totale_speeltijd <- c(57884, 14841, 7709, 5513, 109867)
klassement <- c("Goud", "Brons", "Zilver", "Zilver", "Goud")
console <- c("Switch", "Switch", "Wii", "Wii", "Switch")

df = data.frame(naam, level, totale_speeltijd, klassement, console)

1. Schrijf voor elke vector het type variabele op volgens het schema van Figuur 20.1.

2. Gebruik het commando str(df) om te zien welk datatype R gebruikt voor de verschillende kolommen in dataframe df.

3. Om de data efficiënter te kunnen opslaan en analyseren willen we sommige variabelen omzetten naar een factor. Welke variabelen komen daar het meest voor in aanmerking?

4. Pas de code hierboven aan zodat de vector klassement een factor wordt. Run de aangepaste code in R.

5. Gebruik de functie levels() om te bepalen wat de levels zijn van de vector klassement.

Maten voor ligging en spreiding in R

Centrummaten

Voor het berekenen van gemiddelde en mediaan van een numerieke vector v zijn in R functies ingebouwd:

mean(v)     # gemiddelde
median(v)   # mediaan
summary(v)  # verschillende statistieken voor vector v

Spreidingsmaten

Het bereik, de standaarddeviatie, de variantie, en de IKA van een vector bereken je zo:

range(v) # bereik
sd(v) # standaarddeviatie
var(v) # variantie
IQR(v) # interkwartielafstand (IKA)

Kwantielen

Kwantielen bereken je met de functie quantile(). Als v een vector is, geeft

quantile(v)

de kwartielen weer van die vector. Je kunt ook een specifieke kwantiel opvragen, met het argument prob. Bijvoorbeeld, Q1 of P25 kun je zo berekenen:

quantile(v, prob = 0.25)

Frequentietabellen

Met de functie table() maak je eenvoudig een frequentietabel voor een factor. De frequentietabel voor de burgerlijke staat (MaritalStatus) van de personen in de dataset NHANES maak je zo:

table(NHANES$MaritalStatus)

    Divorced  LivePartner      Married NeverMarried    Separated      Widowed 
         707          560         3945         1380          183          456 

Oefening 20.14 (Frequentietabellen voor een categoriale variabele met R)

In deze opdracht ga je de frequentietabel Tabel 20.2 van de variabele gezondheidsstatus reproduceren in R.

Start een nieuw script en neem de onderstaande code over om de gegevens te importeren:

library("NHANES")   # gebruik het package NHANES
data(NHANES)        # laad de gegevens in een dataframe
gezondheid <- NHANES$HealthGen # kopieer de kolom HealthGen naar een vector

1. Van welk type is variabele gezondheid? Als welk type is deze variabele in R opgeslagen?

   Tip: Voeg str(gezondheid) en levels(gezondheid) toe aan je code.

2. Bekijk de eerste 20 waarden van gezondheid met het commando head(gezondheid, 20). Wat valt je op?

In plaats van een gezondheidstoestand is vaak de waarde NA ingevuld. Dat staat voor “Not Available”; voor deze personen is de gezondheidsstatus dus onbekend.

3. Voeg gezondheid <- na.omit(gezondheid) onderaan je code toe. Wat is er veranderd? Wat doet de functie is.omit()?

4. Voeg gezondheid.t <- table(gezondheid) toe aan je code. Bekijk gezondheid.t. Wat heeft de functie table() gedaan?

5. Bereken nu ook de relatieve frequenties van alle niveaus. Sla deze op in een nieuwe variabele gezondheid.f. Hoe ziet gezondheid.f eruit?

   Tip: Gebruik de functie sum() en het feit dat je een hele tabel kunt delen door een getal.

Grafieken en figuren in R

Een spreidingsdiagram waarin twee numerieke variabelen tegen elkaar worden uitgezet maak je met de functie plot():

x <- c(1, 2, 3)
y <- c(2, 1, 5)
plot(x, y)  # plot alleen punten

Voor een lijndiagram (punten verbonden door lijnen) gebruik je het argument type = "l" of type = "b":

plot(x, y, type = "l") # plot alleen lijnen

plot(x, y, type = "b") # plot punten én lijnen

Een histogram op basis van een numerieke vector maak je zo:

hist( NHANES$Age, breaks = 20 ) # histogram van leeftijden in NHANES

Het argument breaks specificeert het aantal staven, maar R kan daarvan afwijken om de ervoor te zorgen dat de grenzen tussen de klassen een mooi rond getal zijn.

Een staafdiagram maak je op basis van een frequentietabel:

# Maak een frequentietabel
tabel <- table(NHANES$HealthGen)

# Teken het staafdiagram
barplot(tabel)

Oefening 20.15 (Staafdiagram van opleidingsniveau in NHANES)

Schrijf een kort R-script om een staafdiagram te maken van de variabele opleidingsniveau (Education) in de dataset NHANES.

20.15 Samenvatting

Typen variabelen & bijbehorende datatypen in R

Overzicht van typen variabelen

Type variabele		Datatype in R
Numeriek	Continu	numeric
	Discreet	numeric/integer
Categorisch	Nominaal	factor
	Ordinaal	factor

Maten van ligging (centrummaten) van een reeks numerieke waarnemingen

• Modus: Plaats van de piek in de verdeling.

• Mediaan: Middelste waarde na sorteren (bij oneven aantal waarnemingen) of gemiddelde van de middelste twee waarden (bij even aantal waarnemingen).

• Gemiddelde:

  \[\overline{x} = \frac{\sum^n_{i=1}x_i}{n}.\]

Maten van spreiding (spreidingsmaten) van een reeks numerieke waarnemingen

• Bereik: Interval van kleinste tot grootste waarde.

• Kwartielen (Q1, Q2, Q3), percentielen, en kwantielen. (Zie tekst.)

• IKA:

  \[\text{IKA} = \text{Q3} - \text{Q1}.\]

• Variantie:

  \[V_X = \frac{\sum_{i=1}^n \left(x_i - \overline{x}\right)^2}{n-1}.\]

• Standaarddeviatie / -afwijking:

  \[s_X = \sqrt{V_X}=\sqrt{\frac{\sum_i^n \left(x_i - \overline{x}\right)^2}{n-1}}.\]

Frequentietabellen

• Categorische variabelen: Tabel met de (relatieve of absolute) frequenties van ieder niveau.

• Numerieke variabelen: Verdeel het domein eerst in klassen (intervallen); de frequentietabel geeft aan hoe vaak waarnemingen in iedere klasse vallen.

Veelgebruikte diagrammen voor het visualiseren van verdelingen

Overzicht van veelgebruikte diagrammen

Methode	Type variabele	Opmerking
Staafdiagram	categorisch
Taartdiagram	nominaal	Met name geschikt voor relatieve frequenties.
Stapeldiagram	categorisch
Jitterplot	numeriek	Goed voor kleine datasets.
Histogram	numeriek
Frequentiepolygoon	numeriek
Cumulatief frequentiepolygoon	numeriek
Vioolplot	numeriek
Boxplot	numeriek	Vooral geschikt voor unimodale verdelingen, en ongeschikt voor kleine datasets.

20.16 Terminologie

Terminologie over variabelen

Tabel 20.4: Woordenlijst Hoofdstuk 20 (variabelen)

Nederlands	Engels	Beschrijving
beschrijvende statistiek	descriptive statistics	Het onderdeel van statistiek dat zich bezig houdt met het beschrijven van gegevens d.m.v. grafieken, tabellen en kengetallen.
categorische variabele	categorical variable	Variabele met waarden die een groep, label of categorie aanduiden. Synoniem: kwalitatieve variabele.
continue variabele	continuous variable	Een numerieke variabele met reële waarden, zoals een tijdsduur of zoutconcentratie.
discrete variabele	discrete variable	Een numerieke variabel die alleen specifieke waardes kan hebben, zoals gehele getallen.
index	index	Een rangnummer dat we aan elementen uit een verzameling (zoals de waarden in een rij waarnemingen) geven zodat we ernaar kunnen verwijzen.
kengetal	descriptive statistic	Een getal dat een aspect van een reeks gegevens samenvat, zoals het gemiddelde, de som, een proportie, of de standaard deviatie.
kwadratensom	sum of squares	De som van gekwadrateerde afwijkingen van de meetwaarden ten opzichte van het gemiddelde.
nominale variabele	nominal variable	Een categorische variabele waarvan de waarden geen natuurlijke volgorde hebben, zoals soortnamen of kleuren.
numerieke variabele	numerical variable	Variabele die waarvan de waarden getallen zijn (waarmee betekenisvol gerekend kan worden).
ordinale variabele	ordinal variable	Een categorische variabele waarvan de waarden een natuurlijke volgorde hebben, zoals ontwikkelingsstadia.
proportie	proportion	Fractie of deel, aangegeven als een waarde tussen 0 en 1.
spreiding	spread	De mate waarin waarden van een variabele onderling verschillen.
variabele	variable	Een eigenschap van eenheden van een “populatie”.

Terminologie over verdelingen

Tabel 20.5: Woordenlijst Hoofdstuk 20 (verdelingen)

Nederlands	Engels	Beschrijving
absolute frequentie	absolute frequency	Hoe vaak een waarde voorkomt in een bepaalde dataset.
bereik	range	Het interval van de kleinste naar grootste waarde in een reeks waarnemingen.
bimodaal	bimodal	Een verdeling is bimodaal als die twee pieken heeft.
centrummaat	measure of central tendency	Een maat die de ligging van een distributie beschrijft, zoals de modus, de mediaan en het gemiddelde.
gemiddelde	mean	De som van alle waardes in een numerieke dataset, gedeeld door het aantal waarnemingen in die dataset.
ligging	location	Een omschrijving van de positie waar de verdeling van een variabele zich bevindt; wordt beschreven met centrummaten.
mediaan	median	In een georderde rij getallen (van laag naar hoog) de middelste waarde. Gelijk aan het tweede kwartiel Q2, het 50e percentiel P50, en de waarde waar de cumulatieve proportie 0,5 is.
modus	mode	De meest voorkomende waarde in een distributie, of de plek van de “piek” van een histogram.
percentiel	percentile	Kengetal dat gebruikt wordt voor de beschrijving van een verdeling. Per definitie is 75% van de waarden in een verdeling kleiner dan het 75e percentiel, genoteerd als P75.
relatieve frequentie	relative frequency	De frequentie van een waarde, uitgedrukt als proportie van het totaal aantal waarnemingen.
residuen	residuals	Het verschil tussen een datapunt en het gemiddelde van de verdeling.
standaarddeviatie	standard deviation	De “typische” afwijking van het gemiddelde, de meest gebruikte verspreidingsmaat. Synoniem: standaardafwijking
standaardafwijking	standard deviation	De “typische” afwijking van het gemiddelde, de meest gebruikte verspreidingsmaat. Synoniem: standaarddeviatie
scheef	skewed	Een verdeling is scheef als deze een dikkere en/of langer staart heeft in één van de richtingen en dus niet symmetrisch is. Een links-scheve variabele heeft een dikkere/langere staart naar links als deze in een histogram wordt bekeken.
uniform	uniform	Een verdeling waarin iedere uitkomst ongeveer even vaak voorkomt.
unimodaal	unimodal	Een verdeling die één piek heeft.
variantie	variance	De gemiddelde gekwadrateerde afwijking van de waarnemingen ten opzichte van hun gemiddelde.
verdeling (van een variabele)	distribution (of a variable)	De manier waarop de waarden van een variabele over de mogelijk waarden zijn verdeeld.

Terminologie over grafieken en diagrammen

Tabel 20.6: Woordenlijst Hoofdstuk 20 (grafieken en diagrammen)

Nederlands	Engels	Beschrijving
bandbreedte	bandwidth	Een vioolplot geeft de dichtheid van waarnemingen weer in de omgeving van bepaalde waarde. De bandbreedte is de grootte van de omgeving die voor die berekening gebruikt wordt.
boxplot	boxplot	Een diagram dat de verdeling van een variable visualiseert d.m.v. een box (rechthoek) die de kwartielen weergeeft, snorharen, en uitbijters.
cumulatieve verdeling	cumulative distribution	Een functie die aangeeft welk deel van de waarnemingen kleiner is dan een bepaalde waarde.
frequentie	frequency	In een histogram: hoe vaak een variabele een bepaalde waarde aanneemt in de dataset.
frequentiepolygon	frequency polygon	Een lijngrafiek die de frequentie van klassen weergeeft van een numerieke variabele. Vergelijkbaar met een histogram, maar met een lijn in plaats van staven.
frequentietabel	frequency table	Een tabel waarin de frequenties worden weergegeven waarmee de verschillende waarden van een variabele in de waarnemingen voorkomen.
histogram	histogram	Een diagram dat de verdeling van een numerieke variabele visualiseert d.m.v. staven die frequenties weergeven.
interkwartielafstand (IKA)	interquartile range (IQR)	Het verschil in waarde tussen het eerste en het derde kwartiel van een dataset.
jitterplot	jitterplot	Een visualisatie die individuele datapunten toont met willekeurige horizontale of verticale verschuiving (jitter) om overlap te voorkomen.
klasse	bin	Intervallen waarin een continue numerieke variabele opgedeeld wordt om een frequentietabel of histogram te maken.
klokvormig	Bell-shaped	Een verdeling is klokvormig als het histogram de vorm heeft van een kerkklok: een gladde vorm met een hogere frequentie rondom het gemiddelde en aan beide kanten een staart.
kwantiel	quantile	Waarden zoals een percentiel of een kwartiel.
kwartiel	quartile	Een kengetal waarmee verdelingen worden beschreven. Per definitie is een kwart van de gegevens kleiner dan het eerste kwartiel, de helft kleiner dan het tweede kwartiel, en drie kwart kleiner dan het derde kwartiel.
snorharen	whiskers	In een boxplot, de lijnen die vanaf de box naar boven en naar beneden lopen. Ze eindigen bij de verste punten die geen uitbijters zijn.
staafdiagram	bar chart	Een diagram dat de frequenties van een categorische variabele weergeeft als de oppervlakte van staven.
stapeldiagram	stack chart	Een diagram dat de frequenties van een categorische variabele weergeeft als de oppervlakte van staven die op elkaar gestapeld zijn.
taartdiagram	pie chart	Een diagram dat de relatieve frequenties (proporties) van de categorieën van een categorische variabele weergeeft als delen van een cirkel.
uitbijter	outlier	Een waarde die sterk afwijkt van de rest van de verdeling. In een boxplot zijn deze gedefinieerd als waarden die meer dan 1,5 keer de IKA van de box verwijderd zijn.
vioolplot	violin plot	Een grafiek die de verdeling van een variabele weergeeft in een symmetrische figuur waarvan de breedte de dichtheid van waarnemingen aangeeft.
visualiseren	to visualise	In de statistiek: gegevens zichtbaar maken door ze als lengtes, oppervlaktes, kleuren, of vormen af te beelden.

20.17 Opgaven

Oefening 20.16 (Twijfelachtige variabelen)

We hebben geleerd dat variabelen kunnen worden ingedeeld in verschillende categorieën: categoriale variabelen kunnen nominaal of ordinaal zijn, en numerieke variabelen zijn discreet of continu.

1. Kun je je variabelen voorstellen waarbij je kunt discussiëren over de vraag of ze numeriek en discreet zijn, of categoriaal en ordinaal?

2. Kun je je variabelen voorstellen waarbij je kunt discussiëren over de vraag of ze discreet of continu zijn?

3. Kun je je variabelen voorstellen waarbij je kunt discussiëren over de vraag of ze nominaal of ordinaal zijn?

Oefening 20.17 (De twee pieken in de verdeling van lichaamsgewicht)

Figuur 20.7 liet zien dat de verdeling van lichaamsgewicht (Weight) in de dataset NHANES bimodaal is.

Hoe zou dat komen?

Om dat te onderzoeken start je een nieuw script.

1. Schrijf de code die nodig is om de dataset NHANES in een dataframe te laden. (Kijk zo nodig terug naar Oefening 20.14.)

2. Maak nu eerst een histogram van Weight. Verifieer dat de verdeling bimodaal is. Kies een geschikt aantal klassen (met argument breaks).

3. Voeg een regel code toe om een spreidingsdiagram te maken met leeftijd in maanden (AgeMonths) op de \(x\)-as en lichaamsgewicht (Weight) op de \(y\)-as. Gebruik daarvoor de functie plot(); zie Paragraaf 20.14.

   Wat vertelt deze plot je over de oorsprong van de twee pieken?

Oefening 20.18 (De lengte van sprinkhanen)

We bestuderen een aselecte steekproef van vijf sprinkhanen en meten de lichaamslengte van iedere sprinkhaan. We vinden: 3,5 inches, 2,4 inches, 3,4 inches, 3,9 inches, en 2,7 inches.

1. Bereken met de hand gemiddelde, variantie en standaardafwijking van deze waarden. Verifieer je resultaat met R.

2. Hoe veranderen gemiddelde, variantie en standaardafwijking als we van iedere lengte 2 inches aftrekken? Bedenk eerst wat je verwacht, en verifieer dan met R.

3. Hoe veranderen gemiddelde, variantie en standaardafwijking als we de lengte niet in inches maar in centimeters willen uitdrukken? (1 inch = 2,54 cm). Bedenk eerst aan de hand van de formules van gemiddelde, variantie en standaardafwijking wat het antwoord zou moeten zijn; verifieer dan met R.