Oefenvragen

Op deze pagina kun je oefenvragen vinden voor het onderdeel “Biologische Modellen”. Omdat dit een nieuw vak is, zijn er geen oude tentamenvragen beschikbaar, maar ik heb wel een aantal oefenvragen voor jullie gemaakt. Hoewel het tentamen voornamelijk meerkeuze- en invulvragen zal bevatten, zijn de oefenvragen hier in een open vraagvorm. Maar, als je deze vragen kunt beantwoorden, zal een meerkeuzevraag over hetzelfde onderwerp geen probleem zijn!

De antwoorden geef ik nog niet, maar ik zal deze een aantal dagen voor het tentamen op de website zetten. Als je vragen hebt over de vragen, of als je een foutje ziet, laat het me dan weten. (net zoals bij het echte tentamen!)

Oefening 1 (Eiwit in het cytosol) moeilijkheidsgraad: eenvoudig

We modelleren de verandering van een eiwit (“eiwit \(X\)”) in het cytosol. De veranderingen worden uitgedrukt in de hoeveelheid eiwitmoleculen per minuut, gegeven het model:

\(\frac{dX}{dt} = q - lX\)

Wat zijn de eenheden van \(q\) en \(l\)?
Een stamcel begint met een hoeveelheid eiwit \(X=0\), en de parameters zijn bepaald op \(q=3\) en \(l=0.02\). Hoeveel eiwitmoleculen heeft deze cel na lang wachten?

Oefening 2 (Exponentiële groei) moeilijkheidsgraad: gemiddeld

Je hebt 24 uur geleden bacteriën uitgeplaat, en deze zijn allemaal tot kolonies uitgegroeid. Een paar kolonies zijn veel groter dan de rest. Je medestudent zegt: “deze hebben waarschijnlijk een mutatie waardoor ze sneller exponentieel kunnen groeien”. In welke mate ben je het eens/oneens met je medestudent? Licht je antwoord toe.

Oefening 3 (Tegen-intuitief) moeilijkheidsgraad: uitdagend

Helemaal aan het begin van de cursus zijn jullie gewaarschuwd om niet altijd je intuïtie te vertrouwen. Dit is gedurende de hele cursus voorbij gekomen, en zo ook in de laatste hoofdstukken over IBMs en reactie-diffusie systemen (PDEs). Geef voor deze twee type modellen (IBMs/PDEs) een voorbeeld van een tegen-intuitief resultaat. (let op: als je intuitie al is bijgestuurd moet je misschien even doen alsof je dit aan je tante vertelt)

Oefening 4 (Evenwichten in 2D) moeilijkheidsgraad: eenvoudig

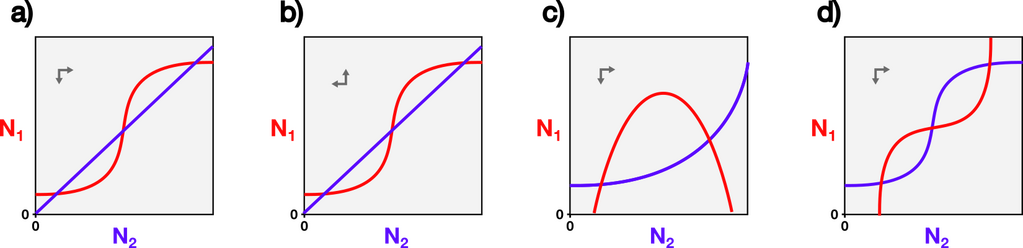
Gegeven faseruimtes met complexe nullclines. Maak met pen en papier de vectorvelden af, en bestudeer de gevonden equilibria. Let goed op de kleuren van de null-clines, en dat er geen nullclines langs de x- en y-as lopen!

Geef voor elke faseruimte aan:

Hoeveel triviale evenwichten zijn er ?
Hoeveel zadelpunten zijn er?
Hoeveel evenwichten zijn stabiel?

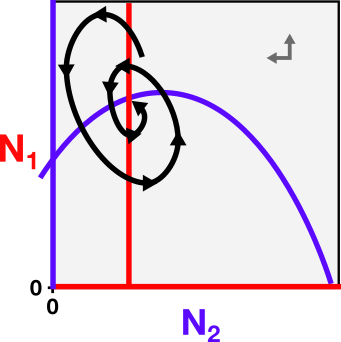
Bekijk ook de onderstaande faseruimte. Een student schetst een trajectorie die eindigt in een stabiel evenwicht, weergegeven met de zwarte pijl. Leg uit waarom deze trajectorie niet correct geschetst is.

Oefening 5 (Virtueel experimenteren) moeilijkheidsgraad: eenvoudig

In Wageningen simuleren ze met zeer grote precisie hoe planten groeien. Hoewel deze modellen complex zijn (en dus een beetje langzaam zijn), zijn er toch belangrijke voordelen aan virtueel experimenteren. Noem twee van deze voordelen.

Oefening 6 (Modelkeuzes) moeilijkheidsgraad: uitdagend

Je hebt in dit cursusonderdeel al over allerlei verschillende modellen geleerd. Zoals in het introductie hoofdstuk uitgelegd, is niet elk model geschikt voor elke situatie. Als je bijvoorbeeld een goed gemengde Erlenmeyer met miljoenen bacteriële cellen modelleert, is een individual-based model met de posities van elk individu misschien niet zo nuttig. Anderzijds kun je zwerm-patronen van slijmschimmels niet modelleren met ODEs, want met ODEs is “een ruimtelijk patroon” niet een van de mogelijke uitkomsten.

Om te oefenen met welk type model past bij welk vraagstuk, staan hieronder een aantal omschrijvingen van biologische systemen die we zouden willen modelleren. Omschrijf voor elk scenario welk type model je zou gebruiken om deze te bestuderen, en motiveer je antwoord. Denk na over het type model (differentievergelijkingen, differentiaalvergelijkingen (ODEs), individual-based models, reactie-diffusie vergelijkingen (PDEs)), maar ook over het type variabele waarmee je de toestand modelleert (discreet, continu, zie Figuur 16.1).

Twee soorten bacteriën ondervinden competitie in een goed gemengde Erlenmeyer.
Twee druppels met fluorescente eiwitten worden op een agar plaat gepipetteerd, waarbij interessante patronen ontstaan.
In een pas afgebrand bos komen pionierssoorten op. De eerste die zich vestigt neemt de ruimte in, waardoor er geen ruimte meer is voor anderen.
Een populatie zooplankton in een goed-gemengd deel van de oceaan ondervindt onderlinge competitie om algen en andere voedselbronnen.
Op de huid van een hagedis vormen zich tijdens de ontwikkeling gevlekte patronen
Een populatie divers gekleurde konijnen wordt door haviken bejaagd
Bacteriële cellen die groeien op een agarplaat kunnen met een kleine kans muteren, en daarbij fluorescent worden
Een morfogen diffundeert door een weefsel van cellen, en activeert daarbij verschillende genexpressiepatronen tijdens de ontwikkeling.
De hoeveelheid paracetamol in het bloed na inname wordt langzaam afgebroken
Na bevruchting ontstaat een calcium-golf op het membraan van de eicel
Een populatie van zeehonden wordt vanuit verschillende hoeken (richtingen) door orca’s belaagd

Oefening 7 (Bacteriën en bacteriofagen) moeilijkheidsgraad: a-c = eenvoudig, d = uitdagend

Bacteriofagen zijn virussen die bacteriën infecteren, en de bacterie daarmee in een virus-fabriek kunnen veranderen. Je collega modelleert dit process met simpele ODEs die de veranderingen in populatiegroottes van bacteriën en virussen beschrijven:

\(\frac{dZ}{dt} = caZY - \delta Z\), en

\(\frac{dY}{dt} = bY(1-\frac{Y}{K}) - dY - aZY\)

Welke vergelijking beschrijft de bacteriën, en welke de virussen?
Omschrijf voor elke term in de vergelijkingen waar deze voor staat.
Je collega meet zorgvuldig alle parameters. De parameter \(c\) heeft een waarde van 10. Leg in biologische begrippen uit wat dit betekent.
Het experiment laat zien dat de bacteriofaag zich in de populatie kan vermenigvuldigen, en dat er daarna een stabiel evenwicht ontstaat waarbij de populaties niet meer veranderen. Je wil weten of het model dezelfde conclusie trekt. Je besluit je de faseruimte te analyseren.

De nullclines voor Z zijn gegeven door: \(Z=0\) en \(Y=\frac{\delta}{ca}\)

De nullclines Y zijn gegeven door: \(Y=0\) en \(Z=\frac{b(1-\frac{Y}{K}) - d}{a}\).

De parameterwaarden zijn: \(c=10, b=2, K=2, a=0.7, \delta=12, d=0.5\).

Voorspelt het model ook dat er een stabiel evenwicht zal zijn van bacteriën en virussen?